Edition 6.1

Dana Lee Ling
Introduction to Statistics Using Google Sheets™
Dana Lee Ling
College of Micronesia-FSM
Pohnpei, Federated States of Micronesia
QA276
Google Sheets™ web-based spreadsheet program © 2018 Google Inc. All rights reserved. Google Sheets is a trademark of Google Incorporated. Google and the Google logo are registered trademarks of Google Inc., used with permission.
Creative Commons -by 4.0
For material not reserved to other owners,
Introduction to Statistics Using Google Sheets™
by Dana Lee Ling is licensed under a Creative Commons Attribution 4.0 International License.
Introduction to Statistics Using Google Sheets™
Table of Contents
Chapters
Google Slides presentations
Stats 01 Introduction Population Samples Levels of Measurement
Stats 02 Measures of middle and spread
Stats 03 Visualizing data
Stats 04 Paired Data and Scatter Diagrams
Stats 05 Probability
Stats 07 Introduction to the Normal Distribution
Stats 08 Sampling distribution of the mean
Stats 09 Confidence intervals
Stats 10 Hypothesis testing
Stats 11 Testing for a difference between two sample means with the t-test
Stats 12 Data exploration
Preface
We all walk in an almost invisible sea of data. I walked into a school fair and noticed a jump rope contest. The number of jumps for each jumper until they fouled out was being recorded on the wall. Numbers. With a mode, median, mean, and standard deviation. Then I noticed that faster jumpers attained higher jump counts than slower jumpers. I saw that I could begin to predict jump counts based on the starting rhythm of the jumper. I used my stopwatch to record the time and total jump count. I later find that a linear correlation does exist, and I am able to show by a t-test that the faster jumpers have statistically significantly higher jump counts. I later incorporated this data into the fall 2007 final.
I walked into a store back in 2003 and noticed that Yamasa™ soy sauce appeared to cost more than Kikkoman™ soy sauce. I recorded Yamasa and Kikkoman soy sauce prices and volumes, working out the cost per milliliter. I eventually showed that the mean price per milliliter for Yamasa was significantly higher than Kikkoman. I also ran a survey of students and determined that the college students prefer Kikkoman to Yamasa.
As a child my son liked articulated mining dump trucks. I found pictures of Terex™ dump trucks on the Internet. I wrote to Terex in Scotland and asked them about how the prices vary for the dump trucks, explaining that I teach statistics and thought that I might be able to use the data in class. "Funny you should ask," a Terex sales representative replied in writing. "The dump trucks are basically priced by a linear relationship between horsepower and price." The representative included a complete list of horsepower and price Terex articulated dump trucks.
One term I learned that a new Cascading Style Sheets level 3 color specification for hue, luminosity, and luminance had been released for HyperText Markup Language web pages. The hues were based on a color wheel with cyan at the 180° middle of the wheel. I knew that Newton had put green in the middle of the red-orange-yellow-green-blue-indigo-violet rainbow, but green is at 120° on a hue color wheel. Green is not the middle of the hue color wheel. And there is no cyan in Newton's rainbow. Could the middle of the rainbow actually be at 180° cyan, or was Newton correct to say the middle of the rainbow is at 120° green? I used a hue analysis tool to analyze the image of an actual rainbow taken by a digital camera here on Pohnpei. This allowed an analysis of the hue angle at the center of the rainbow.
While researching sakau consumption in markets here on Pohnpei I found differences in means between markets, and I found a variation with distance from Kolonia. This implied a relationship between the strength of sakau and the distance from the centrally located town of Kolonia. I asked some of the markets to share their cup tally sheets with me, and a number of the markets obliged. The sakau data suggested that sakau strength was related to the distance from Kolonia.
The point is that we are surrounded by data. You might not go into statistics professionally, yet you will always live in a world filled with data. During this course my hope is that you experience an awareness of the data around you.
Data flows all around you.
A sea of data pours past your senses daily.
A world of data and numbers. Watch for numbers to happen around you. See the matrix.
Curriculum note
The text and the curriculum are an evolving work. Some curriculum options are not specifically laid out in this text. One option is to reserve time at the end of the course to engage in open data exploration. Time can be gained to do this by de-emphasizing chapter five probability, essentially omitting chapter six, and skipping from the end of section 7.2 directly to chapter 8. This material has been retained as these choices should be up to the individual instructor.
For the first time since the inception of the online text, the sections were renumbered from edition 6.0 to 6.1. Content was not changed, but pre-existing links into the text will be broken in places. The section numbers were reworked in some places in part of a move towards support remote learners.
Statistics studies groups of people, objects, or data measurements and produces summarizing mathematical information on the groups. The groups are usually not all of the possible people, objects, or data measurements. The groups are called samples. The larger collection of people, objects or data measurements is called the population.
Statistics attempts to predict measurements for a population from measurements made on the smaller sample. For example, to determine the average weight of a student at the college, a study might select a random sample of fifty students to weigh. Then the measured average weight could be used to estimate the average weight for all student at the college. The fifty students would be the sample, all students at the college would be the population.
Population: The complete group of elements, objects, observations, or people.
Parameters: Measurements of the population: population size N, population median, population mean μ...
Sample: A part of the population. A sample is usually more than five measurements, observations, objects, or people, and smaller than the complete population.
Statistics: Measurements of a sample: sample size n, sample median, sample mean x.
Examples
We could use the ratio of females to males in a class to estimate the ratio of females to males on campus. The sample is the class. The intended population is all students on campus. Whether the statistics class is a "good" sample - representative, unbiased, randomly selected, would be a concern.
We could use the average body fat index for a randomly selected group of females between the ages of 18 and 22 on campus to determine the average body fat index for females in the FSM between the ages of 18 and 22. The sample is those females on campus that we've measured. The intended population is all females between the ages of 18 and 22 in the FSM. Again, there would be concerns about how the sample was selected.
Measurements are made of individual elements in a sample or population. The elements could be objects, animals, or people.
The sample size is the number of elements or measurements in a sample. The lower case letter n is used for sample size. If the population size is being reported, then an upper case N is used. The spreadsheet function for calculating the sample size is the COUNT function.
=COUNT(data)
If one wants to count the sample size for a nominal level list of words, the COUNTA function is used.
=COUNTA(data)
Data can be put into categories such as words or numbers, countable and uncountable, and into levels of measurement.
There are four levels of measurement. In this text most of the data and examples are at the ratio level of measurement.
The levels of measurement can also be thought of as being nested. For example, ratio level data consists of numbers. Numbers can be put in order, hence ratio level data is also orderable data and is thus also ordinal level data. To some extent, each level includes the ones below that level. The highest level of measurement that a data could be considered to be is said to be the level of measurement. There are instances where qualitative data might be placed in an order and thus be considered ordinal data, thus ordinal level data may be either qualitative or quantitative. When a survey says, "Strongly agree, agree, disagree, strongly disagree" the data technically consists of answers which are words. Yet these words have an order, in some instances the answers are mapped to numbers and a median value is then calculated. Above the ordinal level the data is quantitative, numeric data.
Note that at higher levels, such as at the ratio level, the mean is usually chosen to represent the middle, but the median and mode can also be calculated. Statistics that can be calculated at lower levels of measurement can be used in higher levels of measurement.
Descriptive statistics: Numerical or graphical representations of samples or populations. Can include numerical measures such as mode, median, mean, standard deviation. Also includes images such as graphs, charts, visual linear regressions.
Inferential statistics: Using descriptive statistics of a sample to predict the parameters or distribution of values for a population.
The number of measurements, elements, objects, or people in a sample is the sample size n. A simple random sample of n measurements from a population is one selected in a way that:
Ensuring that a sample is random is difficult. Suppose I want to study how many Pohnpeians own cars. Would people I meet/poll on main street Kolonia be a random sample? Why? Why not?
Studies often use random numbers to help randomly selects objects or subjects for a statistical study. Obtaining random numbers can be more difficult than one might at first presume.
Computers can generate pseudo-random numbers. "Pseudo" means seemingly random but not truly random. Computer generated random numbers are very close to random but are actually not necessarily random. Next we will learn to generate pseudo-random numbers using a computer. This section will also serve as an introduction to functions in spreadsheets.
Coins and dice can be used to generate random numbers.
This course presumes prior contact with a course such as CA 100 Computer Literacy where a basic introduction to spreadsheets is made.
The random function RAND generates numbers between 0 and 0.9999...
=rand()
The random number function consists of a function name, RAND, followed by parentheses. For the random function nothing goes between the parentheses, not even a space.
To get other numbers the random function can be multiplied by coefficient. To get whole numbers the integer function INT can be used to discard the decimal portion.
=INT(argument)
The integer function takes an "argument." The argument is a computer term for an input to the function. Inputs could include a number, a function, a cell address or a range of cell addresses. The following function when typed into a spreadsheet that mimic the flipping of a coin. A 1 will be a head, a 0 will be a tail.
=INT(RAND()*2)
The spreadsheet can be made to display the word "head" or "tail" using the following code:
=CHOOSE(INT(RAND()*2),"head","tail")
A single die can also be simulated using the following function
=INT(6*RAND()+1)
To randomly select among a set of student names, the following model can be built upon.
=CHOOSE(INT(RAND()*5+1),"Jan","Jen","Jin","Jon","Jun")
To generate another random choice, press the F9 key on the keyboard. F9 forces a spreadsheet to recalculate all formulas.
When practical, feasible, and worth both the cost and effort, measurements are done on the whole population. In many instances the population cannot be measured. Sampling refers to the ways in which random subgroups of a population can be selected. Some of the ways are listed below.
Census: Measurements done on the whole population.
Sample: Measurements of a representative random sample of the population.
Today this often refers to constructing a model of a system using mathematical equations and then using computers to run the model, gathering statistics as the model runs.
To ensure a balanced sample: Suppose I want to do a study of the average body fat of young people in the FSM using students in the statistics course. The FSM population is roughly half Chuukese, but in the statistics course only 12% of the students list Chuuk as their home state. Pohnpei is 35% of the national population, but the statistics course is more than half Pohnpeian at 65%. If I choose as my sample students in the statistics course, then I am likely to wind up with Pohnpeians being over represented relative to the actual national proportion of Pohnpeians.
| State | 2010 Population | Fractional share of national population (relative frequency) | Statistics students by state of origin spring 2011 | Fractional share of statistics seats |
|---|---|---|---|---|
| Chuuk | 48651 | 0.47 | 10 | 0.12 |
| Kosrae | 6616 | 0.06 | 7 | 0.09 |
| Pohnpei | 35981 | 0.35 | 53 | 0.65 |
| Yap | 11376 | 0.11 | 12 | 0.15 |
| 102624 | 1.00 | 82 | 1.00 |
The solution is to use stratified sampling. I ensure that my sample subgroups reflect the national proportions. Given that the sample size is small, I could choose to survey all ten Chuukese students, seven Pohnpeian students, two Yapese students, and one Kosraean student. There would still be statistical issues of the small subsample sizes from each state, but the ratios would be closer to that seen in the national population. Each state would be considered a single strata.
Used where a population is in some sequential order. A start point must be randomly chosen. Useful in a measuring a timed event. Never used if there is a cyclic or repetitive nature to a system: If the sample rate is roughly equal to the cycle rate, then the results are not going to be randomly distributed measurements. For example, suppose one is studying whether the sidewalks on campus are crowded. If one measures during the time between class periods when students are moving to their next class - then one would conclude the sidewalks are crowded. If one measured only when classes were in session, then one would conclude that there is no sidewalk crowding problem. This type of problem in measurement occurs whenever a system behaves in a regular, cyclical manner. The solution would be ensure that the time interval between measurements is random.
The population is divided into naturally occurring subunits and then subunits are randomly selected for measurement. In this method it is important that subunits (subgroups) are fairly interchangeable. Suppose we want to poll the people in Kitti's opinion on whether they would pay for water if water was guaranteed to be clean and available 24 hours a day. We could cluster by breaking up the population by kousapw and then randomly choose a few kousapw and poll everyone in these kousapw. The results could probably be generalized to all Kitti.
Results or data that are easily obtained is used. Highly unreliable as a method of getting a random samples. Examples would include a survey of one's friends and family as a sample population. Or the surveys that some newspapers and news programs produce where a reporter surveys people shopping in a store.
In science, statistics are gathered by running an experiment and then repeating the experiment. The sample is the experiments that are conducted. The population is the theoretically abstract concept of all possible runs of the experiment for all time.
The method behind experimentation is called the scientific method. In the scientific method, one forms a hypothesis, makes a prediction, formulates an experiment, and runs the experiment.
Some experiments involve new treatments, these require the use of a control group and an experimental group, with the groups being chosen randomly and the experiment run double blind. Double blind means that neither the experimenter nor the subjects know which treatment is the experimental treatment and which is the control treatment. A third party keeps track of which is which usually using number codes. Then the results are tested for a statistically significant difference between the two groups.
Placebo effect: just believing you will improve can cause improvement in a medical condition.
Replication is also important in the world of science. If an experiment cannot be repeated and produce the same results, then the theory under test is rejected.
Some of the steps in an experiment are listed below:
Observational studies gather statistics by observing a system in operation, or by observing people, animals, or plants. Data is recorded by the observer. Someone sitting and counting the number of birds that land or take-off from a bird nesting islet on the reef is performing an observational study.
Surveys are usually done by giving a questionnaire to a random sample. Voluntary responses tend to be negative. As a result, there may be a bias towards negative findings. Hidden bias/unfair questions: Are you the only crazy person in your family?
The process of extending from sample results to population. If a sample is a good random sample, representative of the population, then some sample statistics can be used to estimate population parameters. Sample means and proportions can often be used as point estimates of a population parameter.
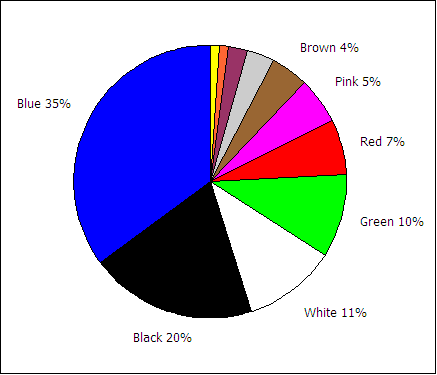
Although the mode and median, covered in chapter three, do not always well predict the population mode and median, there are situations in which a mode may be used. If a good, random, and representative sample of students finds that the color blue is the favorite color for the sample, then blue is a best first estimate of the favorite color of the population of students or any future student sample.
| Favorite color | Frequency f | Relative Frequency or p(color) |
|---|---|---|
| Blue | 32 | 35% |
| Black | 18 | 20% |
| White | 10 | 11% |
| Green | 9 | 10% |
| Red | 6 | 7% |
| Pink | 5 | 5% |
| Brown | 4 | 4% |
| Gray | 3 | 3% |
| Maroon | 2 | 2% |
| Orange | 1 | 1% |
| Yellow | 1 | 1% |
| Sums: | 91 | 100% |
If the above sample of 91 students is a good random sample of the population of all students, then we could make a point estimate that roughly 35% of the students in the population will prefer blue.
The mode is the value that occurs most frequently in the data. Spreadsheet programs can determine the mode with the function MODE.
=MODE(data)
In the Fall of 2000 the statistics class gathered data on the number of siblings for each member of the class. One student was an only child and had no siblings. One student had 13 brothers and sisters. The complete data set is as follows:
1, 2, 2, 2, 2, 2, 3, 3, 4, 4, 4, 5, 5, 5, 7, 8, 9, 10, 12, 12, 13
The mode is 2 because 2 occurs more often than any other value. Where there is a tie there is no mode.
For the ages of students in that class
18, 19, 19, 20, 20, 21, 21, 21, 21, 22, 22, 22, 22, 23, 23, 24, 24, 25, 25, 26
...there is no mode: there is a tie between 21 and 22, hence there no single most frequent value. Spreadsheets will, however, usually report a mode of 21 in this case. Spreadsheets often select the first mode in a multi-modal tie.
If all values appear only once, then there is no mode. Spreadsheets will display #N/A or #VALUE to indicate an error has occurred - there is no mode. No mode is NOT the same as a mode of zero. A mode of zero means that zero is the most frequent data value. Do not put the number 0 (zero) for "no mode." An example of a mode of zero might be the number of children for students in statistics class.
The median is the central (or middle) value in a sorted data set. If a number sits at the middle of a sorted data set, then it is the median. If the middle is between two numbers, then the median is half way between the two middle numbers.
For the sibling data...
1, 2, 2, 2, 2, 2, 3, 3, 4, 4, |4|, 5, 5, 5, 7, 8, 9, 10, 12, 12, 13
...the median is 4.
Remember that the data must be in order (sorted) before you can find the median. For the data 2, 4, 6, 8 the median is 5: (4+6)/2.
The median function in spreadsheets is MEDIAN.
=MEDIAN(data)
The mean, also called the arithmetic mean and also called the average, is calculated mathematically by adding the values and then dividing by the number of values (the sample size n).
If the mean is the mean of a population, then it is called the population mean μ. The letter μ is a Greek lower case "m" and is pronounced "mu."
If the mean is the mean of a sample, then it is the sample mean x. The symbol x is pronounced "x bar."
The sum of the data ∑ x can be determined using the function =SUM(data). The sample size n can be determined using =COUNT(data). Thus =SUM(data)/COUNT(data) will calculate the mean. There is also a single function that calculates the mean. The function that directly calculates the mean is AVERAGE
=AVERAGE(data)
Resistant measures: One that is not influenced by extremely high or extremely low data values. The median tends to be more resistant than mean.
If the mean is measured using the whole population then this would be the population mean. If the mean was calculated from a sample then the mean is the sample mean. Mathematically there is no difference in the way the population and sample mean are calculated.
The midrange is the midway point between the minimum and the maximum in a set of data.
To calculate the minimum and maximum values, spreadsheets use the minimum value function MIN and maximum value function MAX.
=MIN(data)
=MAX(data)
The MIN and MAX function can take a list of comma separated numbers or a range of cells in a spreadsheet. If the data is in cells A2 to A42, then the minimum and maximum can be found from:
=MIN(A2:A42)
=MAX(A2:A42)
The midrange can then be calculated from:
midrange = (maximum + minimum)/2
In a spreadsheet use the following formula:
=(MAX(data)+MIN(data))/2
In addition to measures of the middle, measurements of the spread of data values away from the middle are important in statistical analyses. Spread away from the middle usually involves numeric data values. Perhaps the simplest measures of spread away from the middle involve the smallest value, the minimum, and the largest value, the maximum.
The range is the maximum data value minus the minimum data value. The MIN function returns the smallest numeric value in a data set. The MAX functions returns the largest numeric value in a data set. The difference between the maximum value and the minimum value is called the range.
=MAX(data)−MIN(data)
The range is a useful basic statistic that provides information on the distance between the most extreme values in the data set.
The range does not show if the data if evenly spread out across the range or crowded together in just one part of the range. The way in which the data is either spread out or crowded together in a range is referred to as the distribution of the data. One of the ways to understand the distribution of the data is to calculate the position of the quartiles and making a chart based on the results.
The median is the value that is the middle value in a sorted list of values. At the median 50% of the data values are below and 50% are above. This is also called the 50th percentile for being 50% of the way "through" the data.
If one starts at the minimim, 25% of the way "through" the data, the point at which 25% of the values are smaller, is the 25th percentile. The value that is 25% of the way "through" the data is also called the first quartile.
Moving on "through" the data to the median, the median is also called the second quartile.
Moving past the median, 75% of the way "through" the data is the 75th percentile also known as the third quartile.
Note that the 0th quartile is the minimum and the fourth quartile is the maximum.
Spreadsheets can calculate the first, second, and third quartile for data using a function, the quartile function.
=QUARTILE(data,type)
Data is a range with data. Type represents the type of quartile. (0 = 0% or minimum (zeroth quartile), 1 = 25% or first quartile, 2 = 50% or second quartile (also the median), 3 = 75% or third quartile and 4 = 100% or maximum (fourth quartile). Thus if data is in the cells A1:A20, the first quartile could be calculated using:
=QUARTILE(A1:A20,1)
There are some complex subtleties to calculating the quartile. For a full and thorough treatment of the subject refer to Eric Langford's Quartiles in Elementary Statistics, Journal of Statistics Education Volume 14, Number 3 (2006).
The minimum, first quartile, median, third quartile, and maximum provide a compact and informative five number summary of the distribution of a data set.
The InterQuartile Range (IQR) is the range between the first and third quartile:
=QUARTILE(Data,3) − QUARTILE(Data,1)
There are some subtleties to calculating the IQR for sets with even versus odd sample sizes, but this text leaves those details to the spreadsheet software functions.
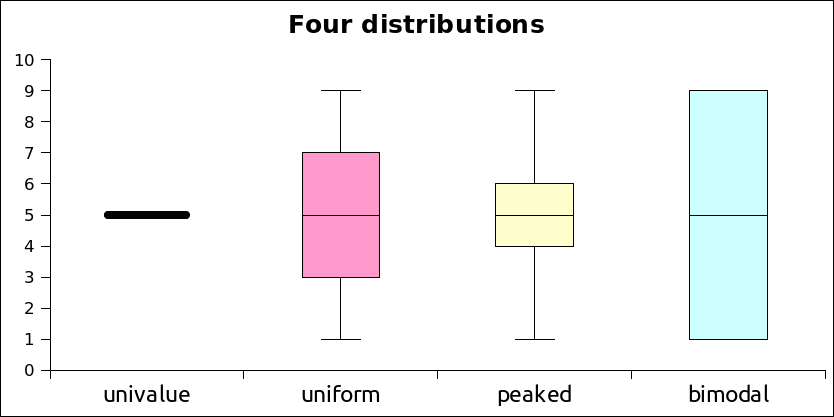
The above is very abstract and hard to visualize. A box and whisker plot takes the above quartile information and plots a chart based on the quartiles. The table below has four different data sets. The first consists of a single value, the second of values spread uniformly across the range, the third has values concentrated near the middle of the range, and the last has most of the values at the minimum or maximum.
| univalue | uniform | peaked symmetric | bimodal |
|---|---|---|---|
| 5 | 1 | 1 | 1 |
| 5 | 2 | 4 | 1 |
| 5 | 3 | 4 | 1 |
| 5 | 4 | 5 | 1 |
| 5 | 5 | 5 | 5 |
| 5 | 6 | 5 | 9 |
| 5 | 7 | 6 | 9 |
| 5 | 8 | 6 | 9 |
| 5 | 9 | 9 | 9 |
Box plots display how the data is spread across the range based on the quartile information above.
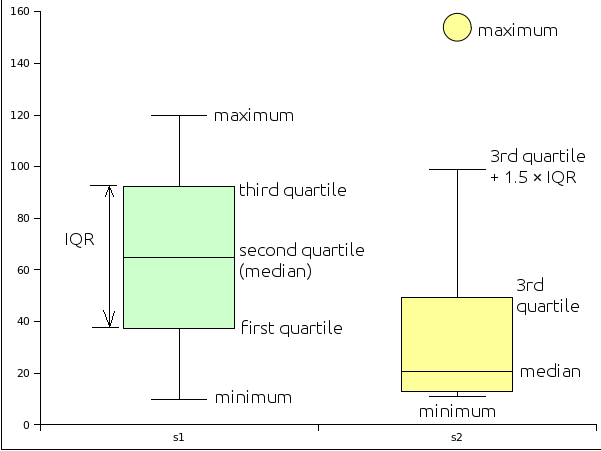
A box and whisker plot is built around a box that runs from the value at the 25th percentile (first quartile) to the value at the 75th percentile (third quartile). The length of the box spans the distance from the value at the first quartile to the third quartile, this is called the Inter-Quartile Range (IQR). A line is drawn inside the box at the location of the 50th percentile. The 50th percentile is also known as the second quartile and is the median for the data. Half the scores are above the median, half are below the median. Note that the 50th percentile is the median, not the mean.
| s1 | s2 |
|---|---|
| 10 | 11 |
| 20 | 11 |
| 30 | 12 |
| 40 | 13 |
| 50 | 15 |
| 60 | 18 |
| 70 | 23 |
| 80 | 31 |
| 90 | 44 |
| 100 | 65 |
| 110 | 99 |
| 120 | 154 |
The basic box plot described above has lines that extend from the first quartile down to the minimum value and from the third quartile to the maximum value. These lines are called "whiskers" and end with a cross-line called a "fence". If, however, the minimum is more than 1.5 × IQR below the first quartile, then the lower fence is put at 1.5 × IQR below the first quartile and the values below the fence are marked with a round circle. These values are referred to as potential outliers - the data is unusually far from the median in relation to the other data in the set.
Likewise, if the maximum is more than 1.5 × IQR beyond the third quartile, then the upper fence is located at 1.5 × IQR above the 3rd quartile. The maximum is then plotted as a potential outlier along with any other data values beyond 1.5 × IQR above the 3rd quartile.
There are actually two types of outliers. Potential outliers between 1.5 × IQR and 3.0 × IQR beyond the fence . Extreme outliers are beyond 3.0 × IQR. In some statistical programs potential outliers are marked with a circle colored in with the color of the box. Extreme outliers are marked with an open circle - a circle with no color inside.
An example with hypothetical data sets is given to illustrate box plots. The data consists of two samples. Sample one (s1) is a uniform distribution and sample two (s2) is a highly skewed distribution.
To generate box plots the online tool BoxPlotR generates box plots including outliers. The first row should be the data label, the variable to be plotted. Data can be copied and pasted into the second tab using the Paste data option. If copying and pasting multiple columns from a spread sheet, preset the separator to Tab. For advanced users notches for the 95% confidence interval for the median can be displayed. The plot can also display the mean and the 95% confidence interval for the mean. The tool is also able to generate violin and bean plots, and change whisker definitions from Tukey to Spear or Altman for advanced users. If the tool grays out, reload the page and recopy the data.
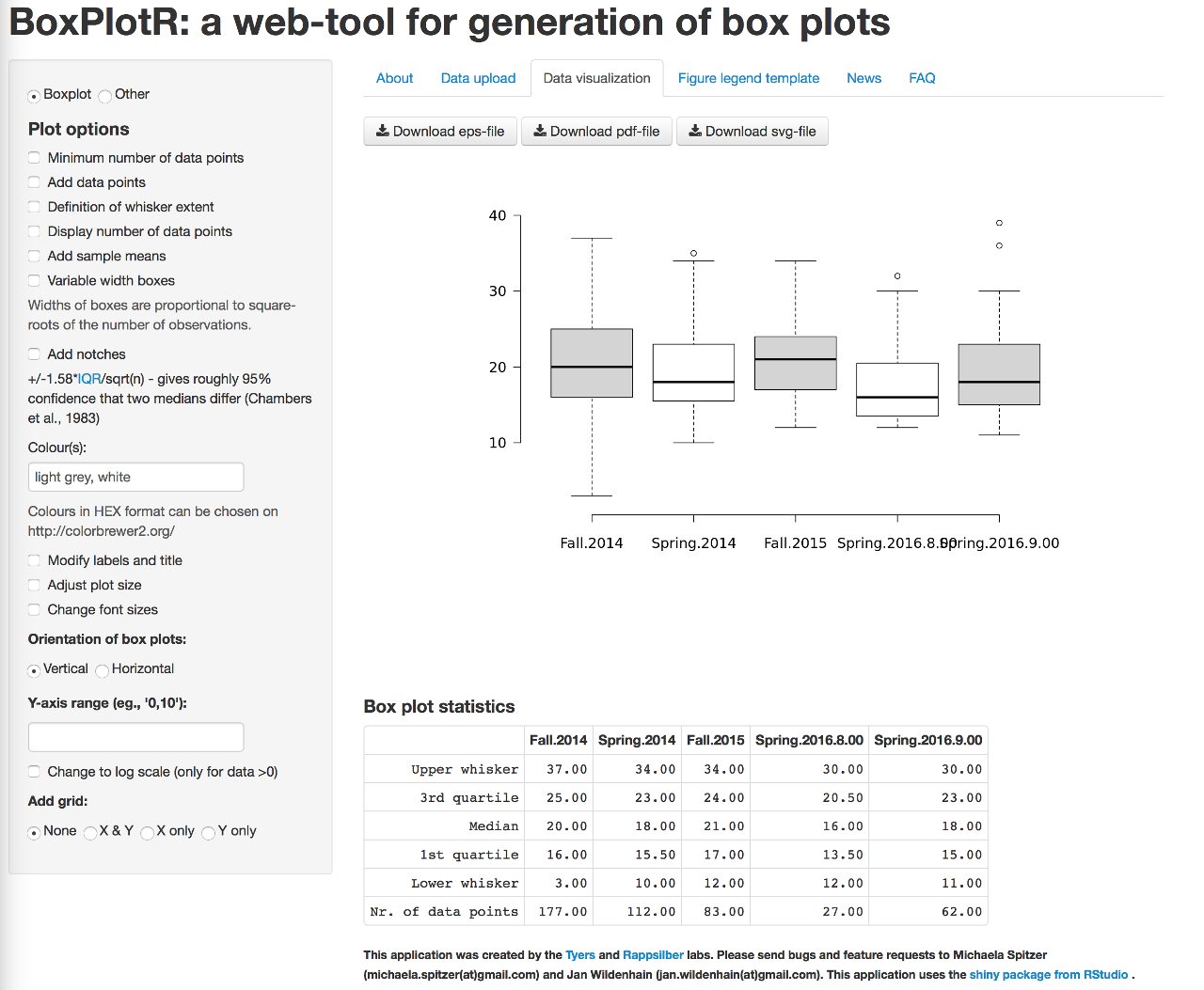
The box and whisker plot is a useful tool for exploring data and determining whether the data is symmetrically distributed, skewed, and whether the data has potential outliers - values far from the rest of the data as measured by the InterQuartile Range. The distribution of the data often impacts what types of analysis can be done on the data.
The distribution is also important to determining whether a measurement that was done is performing as intended. For example, in education a "good" test is usually one that generates a symmetric distribution of scores with few outliers. A highly skewed distribution of scores would suggest that the test was either too easy or too difficult. Outliers would suggest unusual performances on the test.
Consider the following data:
| Data set | |||
|---|---|---|---|
| One | Two | Three | |
| 5 | 1 | 1 | |
| 5 | 3 | 1 | |
| 5 | 5 | 5 | |
| 5 | 7 | 9 | |
| 5 | 9 | 9 | |
| Data set | |||
| One | Two | Three | |
| Mode | 5 | No mode | 1 |
| Median | 5 | 5 | 5 |
| Mean | 5 | 5 | 5 |
| Min | 5 | 1 | 1 |
| Max | 5 | 9 | 9 |
Neither the mode, median, nor the mean reveal clearly the differences in the distribution of the data above. The mean and the median are the same for each data set. The mode is the same as the mean and the median for the first data set. Data set two has no mode. Data set three has a tie causing the mode function to select the number closer to the top of the table as the mode. A single number that would characterize how much the data is spread out would be useful.
As noted earlier, the range is one way to capture the spread of the data. The range is calculated by subtracting the smallest value from the largest value. In a spreadsheet:
=MAX(data)−MIN(data)
The range still does not characterize the difference between data sets 2 and 3. In data set two the data is uniformly spread from the minimum to the maximum. Data set three has more data values at the minimum and the maximum. The range misses this difference in the "internal" spread of the data values.
To capture the spread of the data we use a measure related to the average distance of the data from the mean. We call this the standard deviation. If we have a population, we report this average distance as the population standard deviation. If we have a sample, then our average distance value may underestimate the actual population standard deviation. As a result the formula for sample standard deviation adjusts the result mathematically to be slightly larger. For our purposes these numbers are calculated using spreadsheet functions.
One way to distinguish the difference in the distribution of the numbers in data set 2 and data set 3 above is to use the sample standard deviation.
Note that the sample standard deviation well reflects the larger spread seen in data set three.
The mathematical formula for sample the standard deviation is subtracts the mean from each and every data value, squares that difference, adds up the squares, divides by the sample size n minus one, and then takes the square root of the result.
In spreadsheets there is a single function that performs all of the above operations and calculates the sample standard deviation sx, the STDEV function. The STDEV function is the function that will be used in this course.
=STDEV(data)
In this text the symbol for the sample standard deviation in this text is sx.
In this text the symbol for the population standard deviation is the Greek lower case "s": σ.
The symbol sx usually refers the standard deviation of single variable x data. If there is y data, the standard deviation of the y data is sy. Other symbols that are used for standard deviation include s and σx. Some calculators use the unusual and confusing notations σxn−1 and σxn for sample and population standard deviations.
In this class we always use the sample standard deviation in our calculations. The sample standard deviation is calculated in a way such that the sample standard deviation is slightly larger than the result of the formula for the population standard deviation. This adjustment is needed because a population tends to have a slightly larger spread than a sample. There is a greater probability of outliers in the population data.
The Coefficient of Variation is calculated by dividing the standard deviation (usually the sample standard deviation) by the mean.
=STDEV(data)/AVERAGE(data)
Note that the CV can be expressed as a percentage: Group 2 has a CV of 52% while group 3 has a CV of 69%. A deviation of 3.46 is large for a mean of 5 (3.46/5 = 69%) but would be small if the mean were 50 (3.46/50 = 7%). So the CV can tell us how important the standard deviation is relative to the mean.
As an approximation, the standard deviation for data that has a symmetrical, heap-like distribution is roughly one-quarter of the range. If given only minimum and maximum values for data, this rule of thumb can be used to estimate the standard deviation.
At least 75% of the data will be within two standard deviations of the mean, regardless of the shape of the distribution of the data.
At least 89% of the data will be within three standard deviations of the mean, regardless of the shape of the distribution of the data.
If the shape of the distribution of the data is a symmetrical heap, then as much as 95% of the data will be within two standard deviations of the mean.
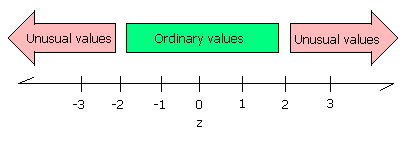
Data beyond two standard deviations away from the mean is considered "unusual" data.
Levels of measurement and appropriate measures
| Level of measurement | Appropriate measure of middle | Appropriate measure of spread |
|---|---|---|
| nominal | mode | none or number of categories |
| ordinal | median | range |
| interval | median or mean | range or standard deviation |
| ratio | mean | standard deviation |
At the interval level of measurement either the median or mean may be more appropriate depending on the specific system being studied. If the median is more appropriate, then the range should be quoted as a measure of the spread of the data. If the mean is more appropriate, then the standard deviation should be used as a measure of the spread of the data.
Another way to understand the levels at which a particular type of measurement can be made is shown in the following table.
Levels at which a particular statistic or parameter has meaning:
| Level of measurement | |||
|---|---|---|---|
| Nominal | Ordinal | Interval | Ratio |
| sample size | |||
| mode | |||
| minimum | |||
| maximum | |||
| range | |||
| median | |||
| mean | |||
| standard deviation | |||
| coefficient of variation | |||
For example, a mode, median, and mean can be calculated for ratio level measures. Of those, the mean is usually considered the best measure of the middle for a random sample of ratio level data.
A variable is defined as any measurement that can take on different data values. Variables are named containers for data values. In statistics variables are often words such as marble color, leaflet length, or marble position.
In a spreadsheet, variables are usually put in row one with the data in the rows below row one. A variable can also have units of measure.
Variables are said to be at the type and level of measurement of the data that the variable contains. Thus variables can be qualitative or quantitative, discrete or continuous. Variables can be at the nominal, ordinal, interval, or ratio level of measurement.
When there are a countable number of values that result from observations, we say the variable producing the results is discrete. The nominal and ordinal levels of measurement almost always measure a discrete variable.
The following examples are typical values for discrete variables:
The last example above is a typical result of a type of survey called a Likert survey developed by Renis Likert in 1932.
When reporting the "middle value" for a discrete distribution at the ordinal level it is usually more appropriate to report the median. For further reading on the matter of using mean values with discrete distributions refer to the pages by Nora Mogey and by the Canadian Psychiatric Association.
Note that if the variable measures only the nominal level of measurement, then only the mode is likely to have any statistical "meaning", the nominal level of measurement has no "middle" per se.
There may be rare instances in which looking at the mean value and standard deviation is useful for looking at comparative performance, but it is not a recommended practice to use the mean and standard deviation on a discrete distribution. The Canadian Psychiatric Association discusses when one may be able to "break" the rules and calculate a mean on a discrete distribution. Even then, bear in mind that ratios between means have no "meaning!"
For example, questionnaire's often generate discrete results:
There are only four possible results for each question. Numeric values (0, 1, 2, 3) could be assigned to the four results, but the numbers would have no particular direct meaning. For example, if the average was 2.5, that would not translate back to a specific number of days per week of usage.
When there is a infinite (or uncountable) number of values that may result from observations, we say that the variable is continuous. Physical measurements such as height, weight, speed, and mass, are considered continuous measurements. Bear in mind that our measurement device might be accurate to only a certain number of decimal places. The variable is continuous because better measuring devices should produce more accurate results.
The following examples are continuous variables:
When reporting the "middle value" for a continuous distribution it is most often appropriate to report the mean and standard deviation. The mean and standard deviation only have "meaning" for the ratio level of measurement.
| Level of measurement | Typical variable type | Typical measure of middle | Typical measure of variation |
|---|---|---|---|
| nominal | discrete | mode | none |
| ordinal | discrete | median | range |
| interval | discrete | median | range |
| ratio | continuous | mean* | sample standard deviation |
*For some ratio level data sets the median may be preferable to the mean. If outliers are known to be likely to be errors in measurement, then the median can produce a better estimate of the middle of a data set.
Z-scores are a useful way to compare or combine scores from data that has different means and standard deviations. Z-scores are an application of the above measures of middle and spread.
Remember that the mean is the result of adding all of the values in the data set and then dividing by the number of values in the data set. The word mean and average are used interchangeably in statistics.
Recall also that the sample standard deviation can be thought of as a mathematical calculation of the average distance of the data from the mean of the data. Note that although I use the words average and mean, the sentence could also be written "the mean distance of the data from the mean of the data."
Z-scores simply indicate how many standard deviations away from the mean is a particular data value. This is termed "relative standing" as it is a measure of where in the data the particular data value is located relative to the mean as counted in units of standard deviations. The formula for calculating the z-score is:
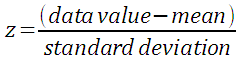
If the population mean µ and population standard deviation σ are known, then the formula for the z-score for a data value x is:
Using the sample mean x and sample standard deviation sx, the formula for a data value x is:
Note the parentheses! When typing in a spreadsheet do not forget the parentheses.
=(value−AVERAGE(data))/STDEV(data)
Data that is two standard deviations below the mean will have a z-score of −2, data that is two standard deviations above the mean will have a z-score of +2. Data beyond two standard deviations away from the mean will have z-scores below −2 or above 2. A data value that has a z-score below −2 or above +2 is considered an unusual value, an extraordinary data value. These values may also be outliers on a box plot depending on the distribution. Box plot outliers and extraordinary z-scores are two ways to characterize unusually extreme data values. There is no simple relationship between box plot outliers and extraordinary z-scores.
Suppose a test has a mean score of 10 and a standard deviation of 2 with a total possible of 20. Suppose a second test has the same mean of 10 and total possible of 20 but a standard deviation of 8.
On the first test a score of 18 would be rare, an unusual score. On the first test 89% of the students would have scored between 6 and 16 (three standard deviations below the mean and three standard deviations above the mean.
On the second test a score of 18 would only be one standard deviation above the mean. This would not be unusual, the second test had more spread.
Adding two scores of 18 and saying the student had a score of 36 out of 40 devalues what is a phenomenal performance on the first test.
Converting to z-scores, the relative strength of the performance on test one is valued more strongly. The z-score on test one would be (18-10)/2 = 4, while on test two the z-score would be (18-10)/8 = 1. The unusually outstanding performance on test one is now reflected in the sum of the z-scores where the first test contributes a sum of 4 and the second test contributes a sum of 1.
When values are converted to z-scores, the mean of the z-scores is zero. A student who scored a 10 on either of the tests above would have a z-score of 0. In the world of z-scores, a zero is average!
Z-scores also adjust for different means due to differing total possible points on different tests.
Consider again the first test that had a mean score of 10 and a standard deviation of 2 with a total possible of 20. Now consider a third test with a mean of 100 and standard deviation of 40 with a total possible of 200. On this third test a score of 140 would be high, but not unusually high.
Adding the scores and saying the student had a score of 158 out of 220 again devalues what is a phenomenal performance on test one. The score on test one is dwarfed by the total possible on test three. Put another way, the 18 points of test one are contributing only 11% of the 158 score. The other 89% is the test three score. We are giving an eight-fold greater weight to test three. The z-scores of 4 and 1 would add to five. This gives equal weight to each test and the resulting sum of the z-scores reflects the strong performance on test one with an equal weight to the ordinary performance on test three.
Z-scores only provide the relative standing. If a test is given again and all students who take the test do better the second time, then the mean rises and like a tide "lifts all the boats equally." Thus an individual student might do better, but because the mean rose, their z-score could remain the same. This is also the downside to using z-scores to compare performances between tests - changes in "sea level" are obscured. One would have to know the mean and standard deviation and whether they changed to properly interpret a z-score.
The table below includes FSM census 2000 data and student seat numbers for the national site of COM-FSM circa 2004.
| State | Population (2000) | Fractional share of national population (relative frequency) | Number of student seats held by state at the national campus | Fractional share of the national campus student seats |
|---|---|---|---|---|
| Chuuk | 53595 | 0.5 | 679 | 0.2 |
| Kosrae | 7686 | 0.07 | 316 | 0.09 |
| Pohnpei | 34486 | 0.32 | 2122 | 0.62 |
| Yap | 11241 | 0.11 | 287 | 0.08 |
| 107008 | 1 | 3404 | 1 |
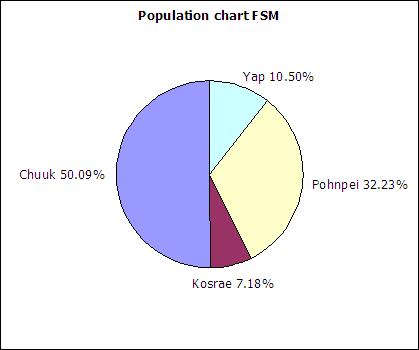
In a circle chart the whole circle is 100% Used when data adds to a whole, e.g. state populations add to yield national population.
A pie chart of the state populations:
The following table includes data from the 2010 FSM census as an update to the above data.
| State | Population (2010) | Relative frequency |
|---|---|---|
| Chuuk | 48651 | |
| Kosrae | 6616 | |
| Pohnpei | 35981 | |
| Yap | 11376 | |
| Sum: | 102624 |
Column charts are also called bar graphs. A column chart of the student seats held by each state at the national site:
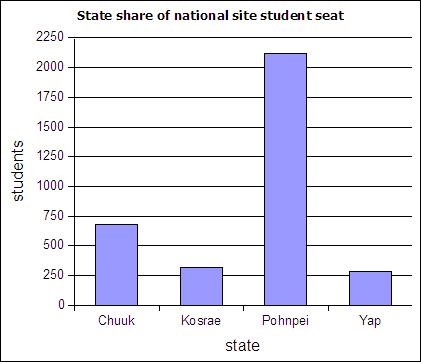
If a column chart is sorted so that the columns are in descending order, then it is called a Pareto chart. Descending order means the largest value is on the left and the values decrease as one moves to the right. Pareto charts are useful ways to convey rank order as well as numerical data.
A line graph is a chart which plots data as a line. The horizontal axis is usually set up with equal intervals. Line graphs are not used in this course and should not be confused with xy scattergraphs.
When you have two sets of continuous data (value versus value, no categories), use an xy graph. These will be covered in more detail in the chapter on linear regressions.
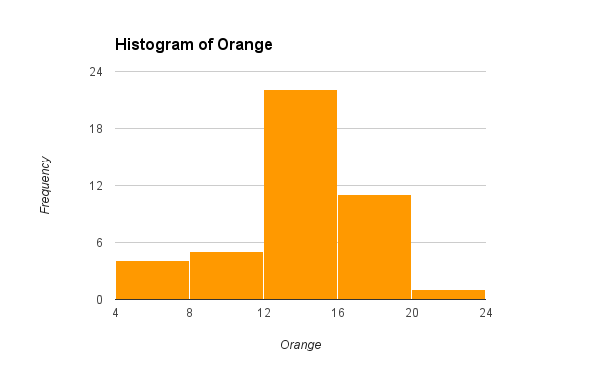
A distribution counts the number of elements of data in either a category or within a range of values. Plotting the count of the elements in each category or range as a column chart generates a chart called a histogram. The histogram shows the distribution of the data. The height of each column shows the frequency of an event. This distribution often provides insight into the data that the data itself does not reveal. In the histogram below, the distribution for male body fat among statistics students has two peaks. The two peaks suggest that there are two subgroups among the men in the statistics course, one subgroup that is at a healthy level of body fat and a second subgroup at a higher level of body fat.
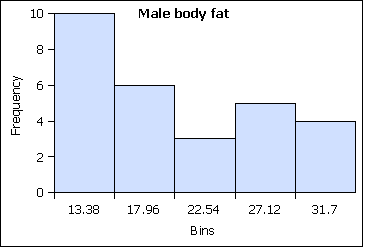
The ranges into which values are gathered are called bins, classes, or intervals. This text tends to use classes or bins to describe the ranges into which the data values are grouped.
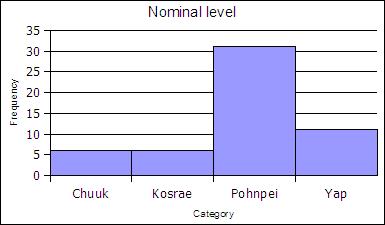
At the nominal level of measurement one can determine the frequency of elements in a category, such as students by state in a statistics course.
| State | Frequency | Relative Frequency |
|---|---|---|
| Chuuk | 6 | 0.11 |
| Kosrae | 6 | 0.11 |
| Pohnpei | 31 | 0.57 |
| Yap | 11 | 0.20 |
| Sums: | 54 | 1.00 |
The sum of the frequencies is the sample size.
The sum of the relative frequencies is always one.
The sum of the frequencies being the sample size and the sum of the relative frequencies being one are ways to check your frequency table.
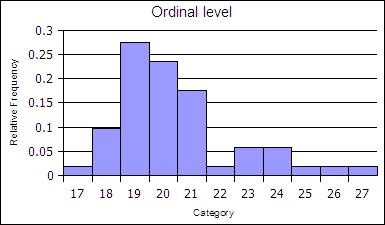
At the ordinal level, a frequency distribution can be done using the rank order, counting the number of elements in each rank order to obtain a frequency. When the frequency data is calculated in this way, the distribution is not grouped into a smaller number of classes. Note that some classes could be empty - the classes must still be equal width.
| Age | Frequency | Rel Freq |
|---|---|---|
| 17 | 1 | 0.02 |
| 18 | 5 | 0.1 |
| 19 | 14 | 0.27 |
| 20 | 12 | 0.24 |
| 21 | 9 | 0.18 |
| 22 | 1 | 0.02 |
| 23 | 3 | 0.06 |
| 24 | 3 | 0.06 |
| 25 | 1 | 0.02 |
| 26 | 1 | 0.02 |
| 27 | 1 | 0.02 |
| sums | 51 | 1 |
The ranks can be collected together, classed, to reduce the number of rank order categories. in the example below the age data in gathered into two-year cohorts.
| Age | Frequency | Rel Freq |
|---|---|---|
| 19 | 20 | 0.39 |
| 21 | 21 | 0.41 |
| 23 | 4 | 0.08 |
| 25 | 4 | 0.08 |
| 27 | 2 | 0.04 |
| Sums: | 51 | 1 |
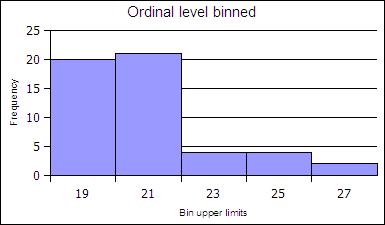
Ratio level data is usually a continuous variable. The number of possible values cannot be counted. At the ratio level data is divided into intervals of equal width from the minimum value to the maximum value. The intervals are called classes by statisticians. The intervals are called buckets in Google Sheets™.
Google Sheets™ can automatically generate a histogram chart from raw data. The specific dialog boxes tend to change in terms of layout and new edit capabilities appear over time.
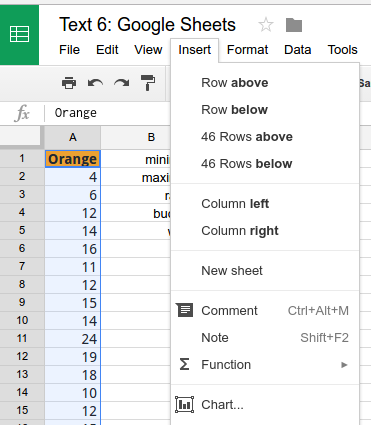
Pre-select the data range and from the Insert menu choose Chart.
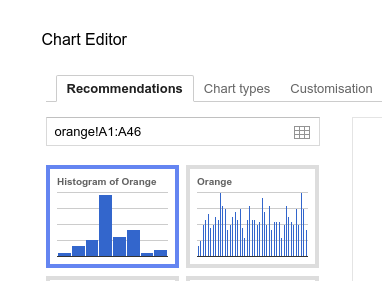
Choose the histogram chart option.
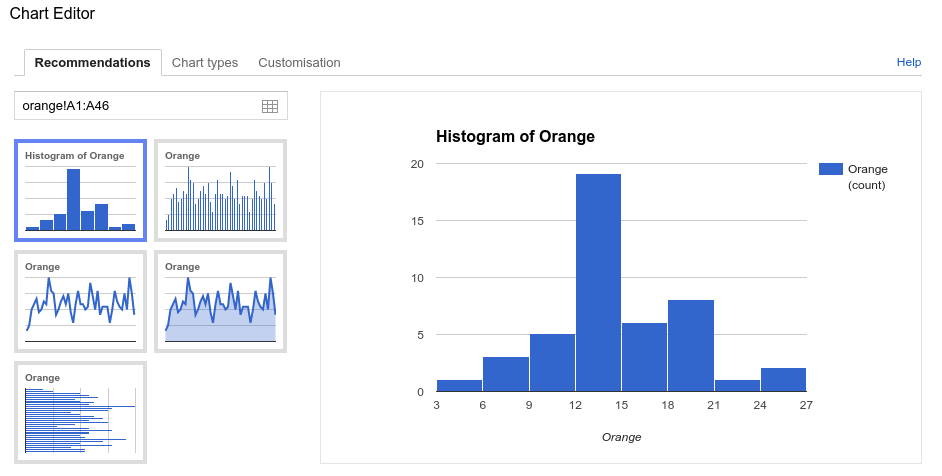
At this point the histogram chart could be inserted into the spread sheet using the automatically chosen number of classes (buckets).
Google Sheets™ also provides the option to specify the number of classes (buckets).
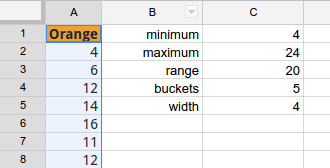
To generate a histogram with a specific number of classes, determine the minimum, maximum, and range. Divide the range by the number of desired classes (buckets) to obtain the class width. In the following example a five bucket histogram chart was desired.
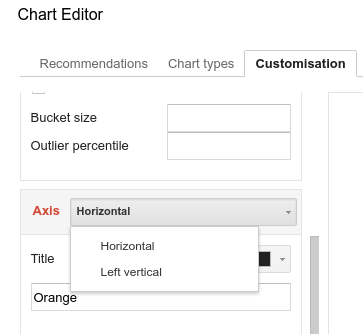
With the Axis set to Horizontal...
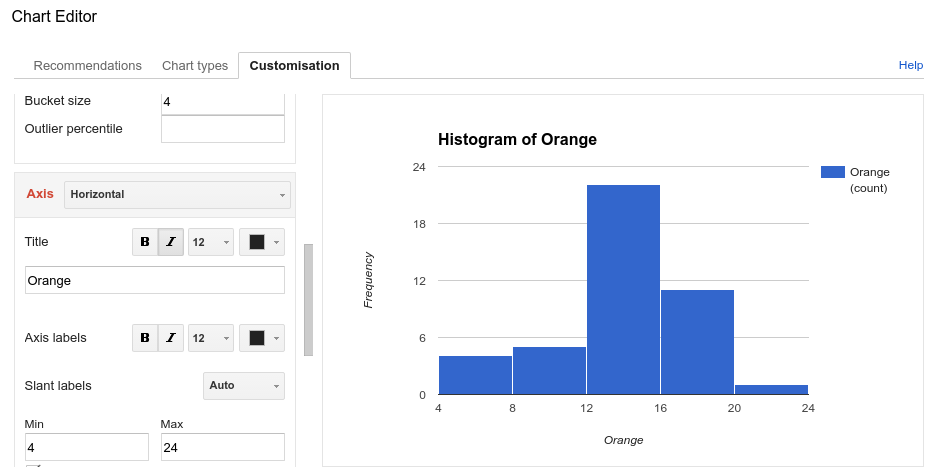
Enter the width as the bucket size. Further below enter the minimum value, and maximum values.
Insert.
Google and the Google logo are registered trademarks of Google Inc., used with permission.
Each bucket has a smallest value called the class lower limit. Each bucket has a largest value called a class upper limit. The number of data values in each bucket is called the frequency. Spreadsheets have a FREQUENCY function that uses the class upper limits to automatically count the frequencies for each bucket.
To calculate the class upper limits the minimum and maximum value in a data set must be determined. Spreadsheets include functions to calculate the minimum value MIN and maximum value MAX in a data set.
=MIN(data)
=MAX(data)
The minimum and maximum are used to calculate the range. The width of each bucket is equal to the range divided by the number of desired buckets.
| Class Upper Limits (CUL) | Frequency |
| =min + class width | |
| + class width | |
| + class width | |
| + class width | |
| + class width = max |
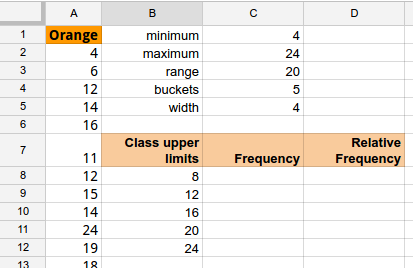
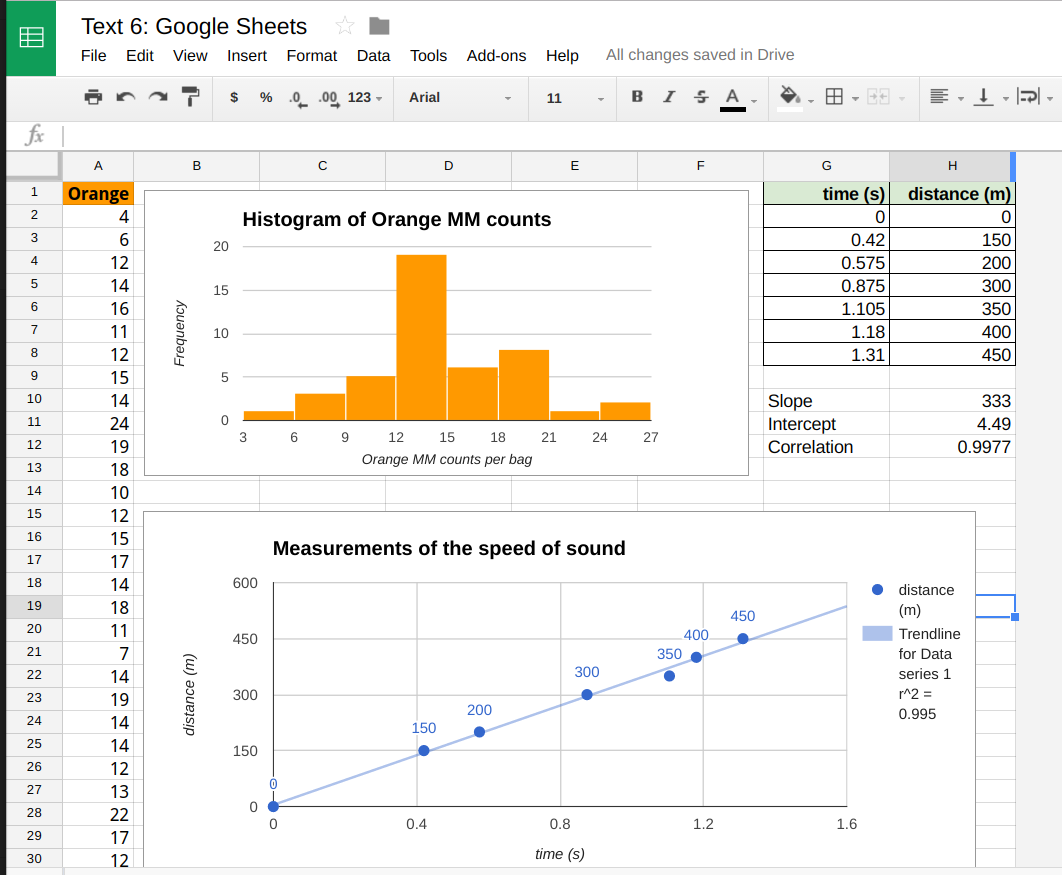
For the Orange MM data determine the minimum and maximum. Calculate the range. For a five class (bucket) frequency table, divide the range by five to obtain the width. Use the table above to enter the class upper limits.

Pre-select the cells into which the FREQUENCY array function will place the frequencies. Note that one selects all of the cells before typing the formula!
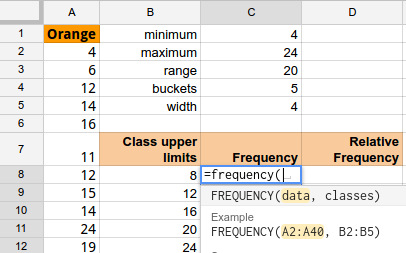
Then enter the formula.
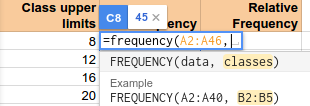
Select or type in the spreadsheet addresses containing the data.

Type a comma, and then enter the spreadsheet addresses containing the class upper limits.
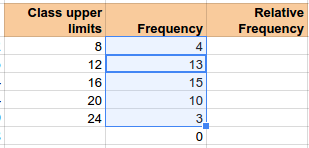
Close the parentheses and press enter.
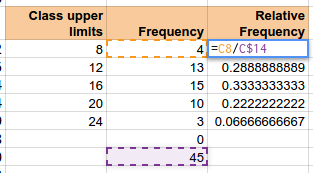
Relative frequencies can be added in a third column.
As noted above:
The sum of the frequencies is the sample size.
The sum of the relative frequencies is always one.
The sum of the frequencies being the sample size and the sum of the relative frequencies being one are ways to check your frequency table.
Google and the Google logo are registered trademarks of Google Inc., used with permission.
The shapes of distributions have names by which they are known.
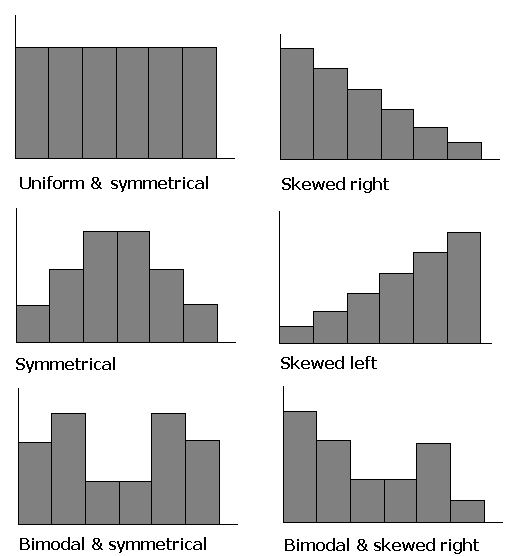
One of the aspects of a sample that is often similar to the population is the shape of the distribution. If a good random sample of sufficient size has a symmetric distribution, then the population is likely to have a symmetric distribution. The process of projecting results from a sample to a population is called generalizing. Thus we can say that the shape of a sample distribution generalizes to a population.
| uniform | peaked symmetric | skewed |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 5 | 5 |
| 3 | 7 | 8 |
| 4 | 9 | 9 |
| 5 | 10 | 11 |
| 6 | 11 | 12 |
| 7 | 12 | 13 |
| 8 | 12 | 14 |
| 9 | 13 | 15 |
| 10 | 13 | 16 |
| 11 | 14 | 17 |
| 12 | 14 | 18 |
| 13 | 14 | 19 |
| 14 | 14 | 20 |
| 15 | 15 | 20 |
| 16 | 15 | 21 |
| 17 | 15 | 22 |
| 18 | 15 | 23 |
| 19 | 16 | 24 |
| 20 | 16 | 23 |
| 21 | 17 | 24 |
| 22 | 17 | 25 |
| 23 | 18 | 26 |
| 24 | 19 | 27 |
| 25 | 20 | 25 |
| 26 | 22 | 26 |
| 27 | 24 | 27 |
| 28 | 28 | 28 |
Both box plots and frequency histograms show the distribution of the data. Box plots and frequency histograms are two different views of the distribution of the data. There is a relationship between the frequency histogram and the associated box plot. The following charts show the frequency histograms and box plots for three distributions: a uniform distribution, a peaked symmetric heap distribution, and a left skewed distribution.
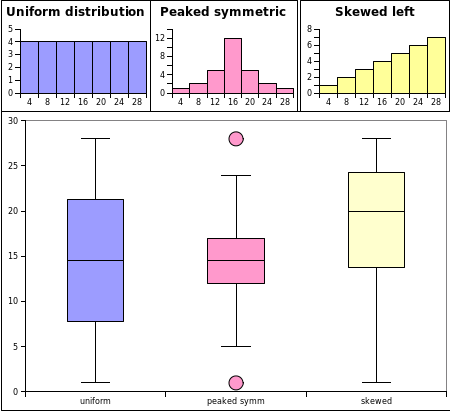
The uniform data is evenly distributed across the range. The whiskers run from the maximum to minimum value and the InterQuartile Range is the largest of the three distributions.
The peaked symmetric data has the smallest InterQuartile Range, the bulk of the data is close to the middle of the distribution. In the box plot this can be seen in the small InterQuartile range centered on the median. The peaked symmetric data has two potential outliers at the minimum and maximum values. For the peaked symmetric distribution data is usually found near the middle of the distribution.
The skewed data has the bulk of the data near the maximum. In the box plot this can be seen by the InterQuartile Range - the box - being "pushed" up towards the maximum value. The whiskers are also of an unequal length, another sign of a skewed distribution.
Some distributions are considered "pathological" in the sense that they are not statistically "well-behaved." Such distributions are problematic for the normal curve statistical analyses that are done later in this course. For example, two highly skewed distributions with extreme outliers can have the same mean but a different median. The pathology of the two data sets is a result of the impact of outliers on the mean. Outliers do not impact the median as much as they do the mean. Hence the mean is said to be sensitive to outliers while the median is said to be insensitive to outliers.
A runner runs from the College of Micronesia-FSM National campus to PICS via the powerplant/Nanpohnmal back road. The runner tracks his time and distance.
| Location | Time x (minutes) | Distance y (km) |
|---|---|---|
| College | 0 | 0 |
| Dolon Pass | 20 | 3.3 |
| Turn-off for Nanpohnmal | 25 | 4.5 |
| Bottom of the beast | 33 | 5.7 |
| Top of the beast | 34.5 | 5.9 |
| Track West | 55 | 9.7 |
| PICS | 56 | 10.1 |
Is there a relationship between the time and the distance? If there is a relationship,
then data will fall in a patterned fashion on an xy graph. If there is no relationship,
then there will be no shape to the pattern of the data on a graph.
If the relationship is linear, then the data will fall roughly along a line. Plotting the
above data yields the following graph:
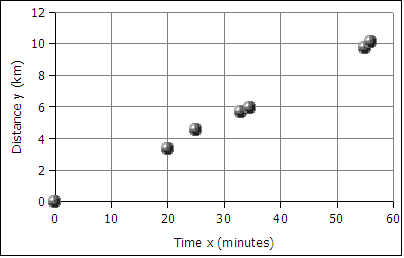
The data falls roughly along a line, the relationship appears to linear. If we can find the equation of a line through the data, then we can use the equation to predict how long it will take the runner to cover distances not included in the table above, such as five kilometers. In the next image a best fit line has been added to the graph.
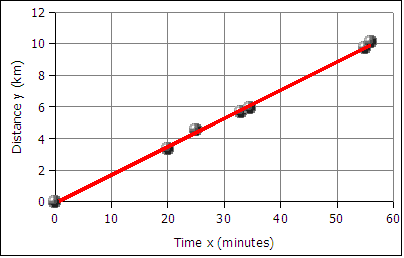
The best fit line is also called the least squares line because the mathematical process for determining the line minimizes the square of the vertical displacement of the data points from the line. The process of determining the best fit line is also known and performing a linear regression. Sometimes the line is referred to as a linear regression.
The graph of time versus distance for a runner is a line because a runner runs at the same pace kilometer after kilometer.
For paired data the sample size n is the number of pairs. This is usually also the number of rows in the data table. Do NOT count both the x and y values, the (x,y) data should be counted in pairs.
A spreadsheet is used to find the slope and the y-intercept of the best fit line through the data.
To get the slope m use the function:
=SLOPE(y-values,x-values)
Note that the y-values are entered first, the x-values are entered second. This is the reverse of traditional algebraic order where coordinate pairs are listed in the order (x, y). The x and y-values are usually arranged in columns. The column containing the x data is usually to the left of the column containing the y-values. An example where the data is in the first two columns from row two to forty-two can be seen below.
=SLOPE(B2:B42,A2:A42)
The intercept is usually the starting value for a function. Often this is the y data value at time zero, or distance zero.
To get the intercept:
=INTERCEPT(y-values,x-values)
Note that intercept also reverses the order of the x and y values!
For the runner data above the equation is:
distance = slope * time + y-intercept
distance = 0.18 * time + − 0.13
y = 0.18 * x + − 0.13
or
y = 0.18x − 0.13
where x is the time and y is the distance
In algebra the equation of a line is written as y = m*x + b where m is the slope and b is the intercept. In statistics the equation of a line is written as y = a + b*x where a is the intercept (the starting value) and b is the slope. The two fields have their own traditions, and the letters used for slope and intercept are a tradition that differs between the field of mathematics and the field of statistics.
Using the y = mx + b equation we can make predictions about how far the runner will travel given a time, or how long a duration of time the runner will run given a distance. For example, according the equation above, a 45 minute run will result in the runner covering 0.18*45 - 0.13 = 7.97 kilometers. Using the inverse of the equation we can predict that the runner will run a five kilometer distance in 28.5 minutes (28 minutes and 30 seconds).
Given any time, we can calculate the distance. Given any distance, we can solve for the time.
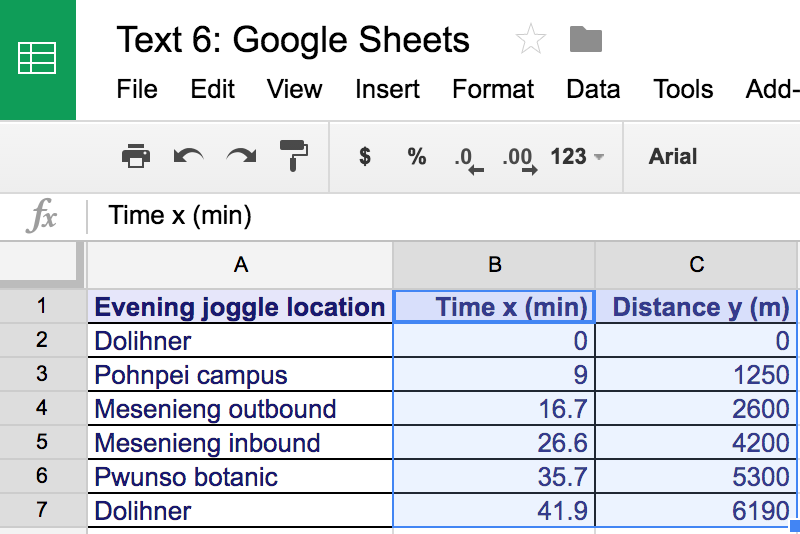
The data used in the following examples is contained in the following table.
| Evening joggle (run+juggle) location | Time x (min) | Distance y (m) |
|---|---|---|
| Dolihner | 0.0 | 0 |
| Pohnpei campus | 9.0 | 1250 |
| Mesenieng outbound | 16.7 | 2600 |
| Mesenieng inbound | 26.6 | 4200 |
| Pwunso botanic | 35.7 | 5300 |
| Dolihner | 41.9 | 6190 |
First select the data to be graphed.
Choose either Insert: Chart or click on the Insert Chart icon on the menubar.
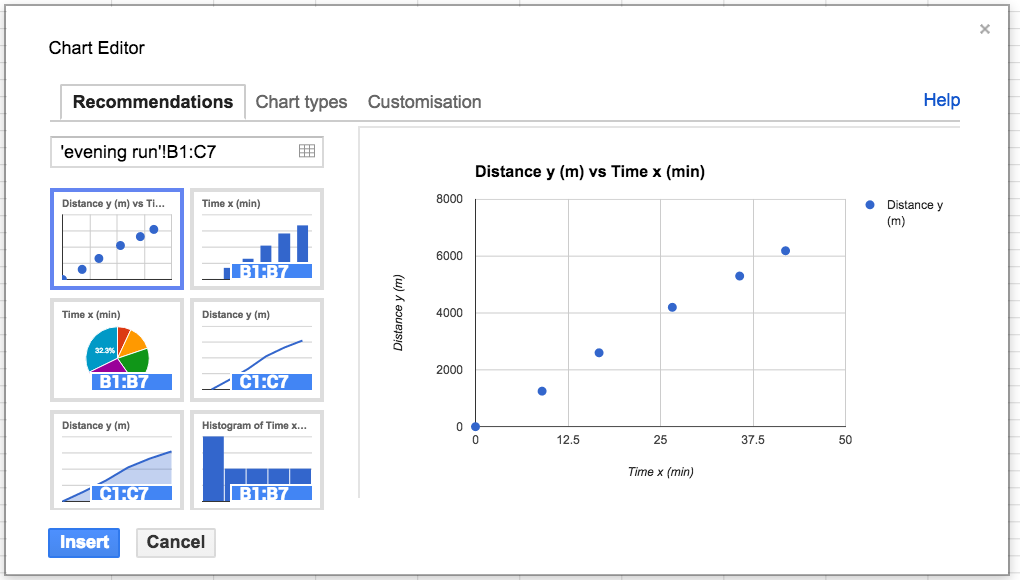
Choose the xy scatter graph in the Chart Editor. The chart editor's third tab, Customization, can be used to display the equation of the line. The trendline options are at the bottom of the dialog box.
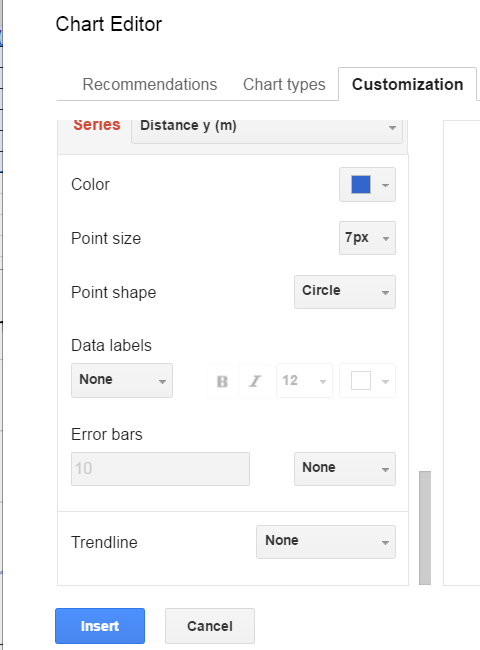
Options include linear, exponential, and polynomial. In this text linear trendlines are used.
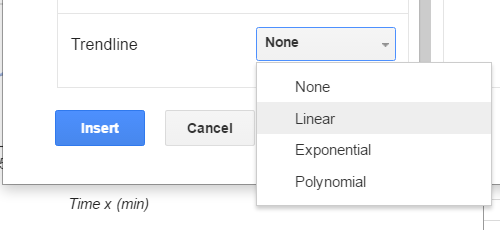
Once the linear option is chosen, the dialog box expands to show other options including displaying the trendline and R². R² is covered later in this chapter.
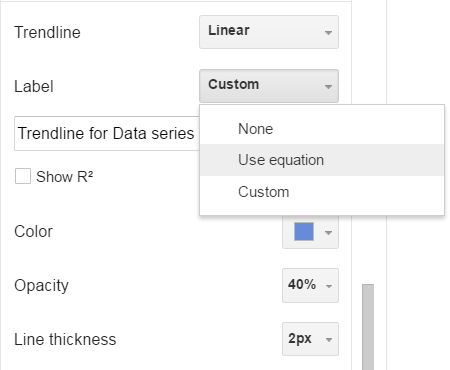
The location of the legend can also be selected to "unwrap" the equation of the line. In some legend locations the legend might not display both the equation and the R² value.
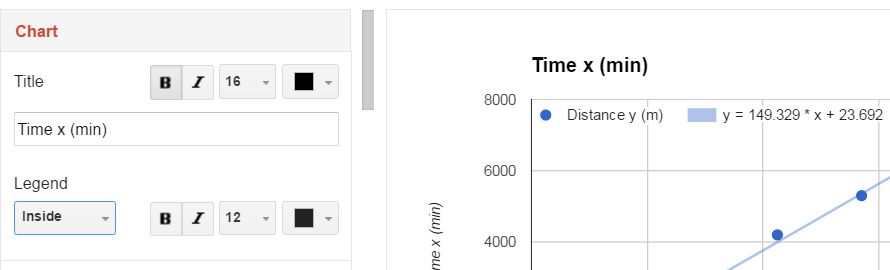
Google and the Google logo are registered trademarks of Google Inc., used with permission.
The LINEST array function in Google Sheets™ can be used, =LINEST(y-data,x-data,true,true) to obtain the statistics necessary to construct 95% confidence intervals for the slope and intercept. This example uses the same evening run data provided above.
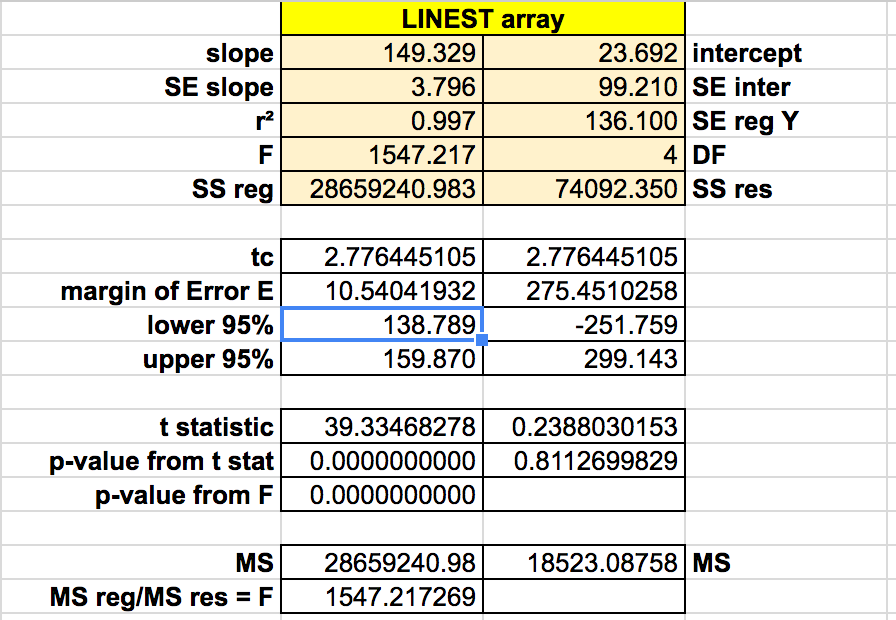
After plotting the x and y data, the xy scattergraph helps determine the nature of the relationship between the x values and the y values. If the points lie along a straight line, then the relationship is linear. If the points form a smooth curve, then the relationship is non-linear (not a line). If the points form no pattern then the relationship is random.
Relationships between two sets of data can be positive: the larger x gets, the larger y
gets.
Relationships between two sets of data can be negative: the larger x gets, the smaller y
gets.
Relationships between two sets of data can be non-linear
Relationships between two sets of data can be random: no relationship exists!
For the runner data above, the relationship is a positive relationship. The points line along a line, therefore the relationship is linear.
An example of a negative relationship would be the number of beers consumed by a student and a measure of the physical coordination. The more beers consumed the less their coordination!
For a linear relationship, the closer to a straight line the points fall, the stronger the relationship. The measurement that describes how closely to a line are the points is called the correlation.

The following example explores the correlation between the distance of a business from a city center versus the amount of product sold per person. In this case the business are places that serve pounded Piper methysticum plant roots, known elsewhere as kava but known locally as sakau. This business is unique in that customers self-limit their purchases, buying only as many cups of sakau as necessary to get the warm, sleepy, feeling that the drink induces. The businesses are locally referred to as sakau markets. The local theory is that the further one travels from the main town (and thus deeper into the countryside of Pohnpei) the stronger the sakau that is served. If this is the case, then the mean number of cups should fall with distance from the main town on the island.
The following table uses actual data collected from these businesses, the names of the businesses have been changed.
| Sakau Market | distance/km (x) | mean cups per person (y) |
|---|---|---|
| Upon the river | 3.0 | 5.18 |
| Try me first | 13.5 | 3.93 |
| At the bend | 14.0 | 3.19 |
| Falling down | 15.5 | 2.62 |
The first question a statistician would ask is whether there is a relationship between the distance and mean cup data. Determining whether there is a relationship is best seen in an xy scattergraph of the data.
If we plot the points on an xy graph using a spreadsheet, the y-values can be seen to fall with increasing x-value. The data points, while not all exactly on one line, are not far away from the best fit line. The best fit line indicates a negative relationship. The larger the distance, the smaller the mean number of cups consumed.
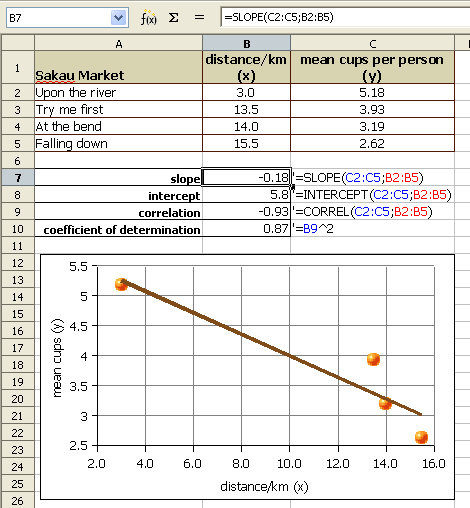
We use a number called the Pearson product-moment correlation coefficient r to tell us how well the data fits to a straight line. The full name is long, in statistics this number is called simply r. R can be calculated using a spreadsheet function.
The function for calculating r is:
=CORREL(y-values,x-values)
Note that the order does not technically matter. The correlation of x to y is the same as that of y to x. For consistency the y-data,x-data order is retained above.
The Pearson product-moment correlation coefficient r (or just correlation r) values that result from the formula are always between -1 and 1. One is perfect positive linear correlation. Negative one is perfect negative linear correlation. If the correlation is zero or close to zero: no linear relationship between the variables.
A guideline to r values:

Note that perfect has to be perfect: 0.99999 is very close, but not perfect. In real world systems perfect correlation, positive or negative, is rarely or never seen. A correlation of 0.0000 is also rare. Systems that are purely random are also rarely seen in the real world.
Spreadsheets usually round to two decimals when displaying decimal numbers. A correlation r of 0.999 is displayed as "1" by spreadsheets. Use the Format menu to select the cells item. In the cells dialog box, click on the numbers tab to increase the number of decimal places. When the correlation is not perfect, adjust the decimal display and write out all the decimals.
The correlation r of − 0.93 is a strong negative correlation. The relationship is strong and the relationship is negative. The equation of the best fit line, y = −0.18x + 5.8 where y is the mean number of cups and x is the distance from the main town. The equations that generated the slope, y-intercept, and correlation can be seen in the earlier image.
The strong relationship means that the equation can be used to predict mean cup values, at least for distances between 3.0 and 15.5 kilometers from town.
A second example is drawn from body fat data. The following chart plots age in years for female statistics students against their body fat index.
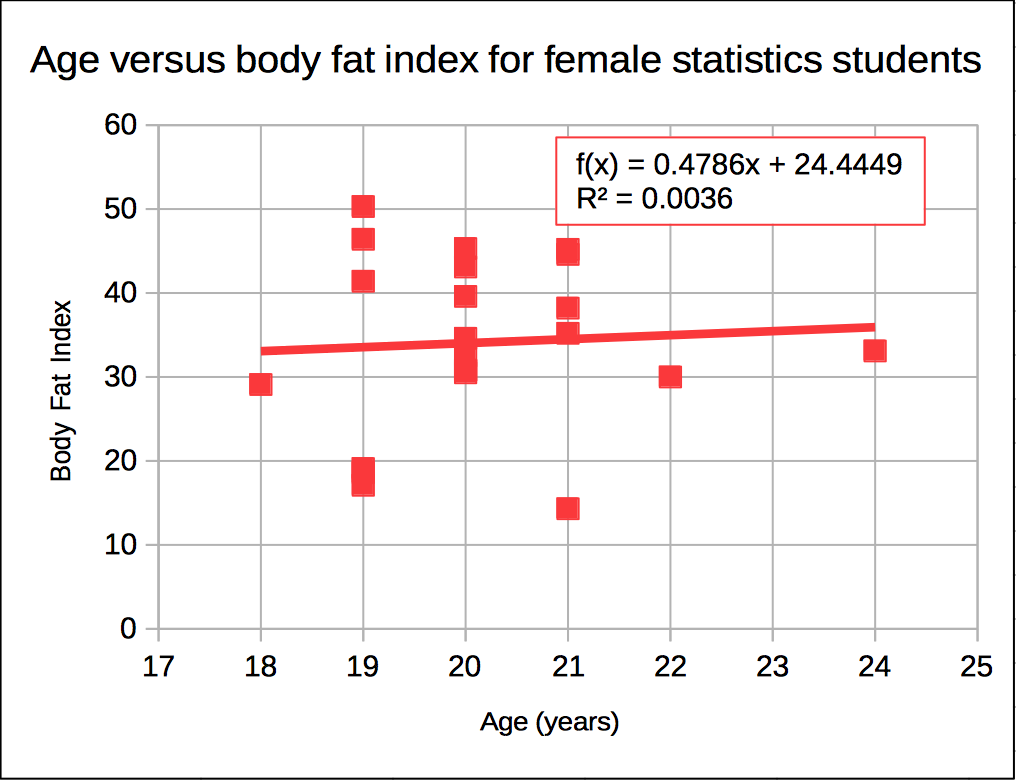
Is there a relationship seen in the xy scattergraph between the age of a female statistics student and the body fat index? Can we use the equation to predict body fat index on age alone?
If we plot the points on an xy graph using a spreadsheet as seen above, the data does not appear to be linear. The data points do not form a discernable pattern. The data appears to be scattered randomly about the graph. Although a spreadsheet is able to give us a best fit line (a linear regression or least squares line), that equation will not be useful for predicting body fat index based on age.
In the example above the correlation r can be calculated and is found to be 0.06. Zero would be random correlation. This value is so close to zero that the correlation is effectively random. The relationship is random. There is no relationship. The linear equation cannot be used to predict the body fat index given the age.
We cannot usually predict values that are below the minimum x or above the maximum x values and make meaningful predictions. In the example of the runner, we could calculate how far the runner would run in 72 hours (three days and three nights) but it is unlikely the runner could run continuously for that length of time. For some systems values can be predicted below the minimum x or above the maximum x value. When we do this it is called extrapolation. Very few systems can be extrapolated, but some systems remain linear for values near to the provided x values.
Image credit: xkcd under a Creative Commons Attribution-NonCommercial 2.5 license. Some rights reserved.
The coefficient of determination, r², is a measure of how much of the variation in the independent x variable explains the variation in the dependent y variable. This does NOT imply causation. In spreadsheets the ^ symbol (shift-6) is exponentiation. In spreadsheets we can square the correlation with the following formula:
=(CORREL(y-values,x-values))^2
The result, which is between 0 and 1 inclusive, is often expressed as a percentage.
Imagine a Yamaha outboard motor fishing boat sitting out beyond the reef in an open ocean swell. The swell moves the boat gently up and down. Now suppose there is a small boy moving around in the boat. The boat is rocked and swayed by the boy. The total motion of the boat is in part due to the swell and in part due to the boy. Maybe the swell accounts for 70% of the boat's motion while the boy accounts for 30% of the motion. A model of the boat's motion that took into account only the motion of the ocean would generate a coefficient of determination of about 70%.
Finding that a correlation exists does not mean that the x-values cause the y-values. A line does not imply causation: Your age does not cause your pounds of body fat, nor does time cause distance for the runner.
Studies in the mid 1800s of Micronesia would have shown of increase each year in church attendance and sexually transmitted diseases (STDs). That does NOT mean churches cause STDs! What the data is revealing is a common variable underlying our data: foreigners brought both STDs and churches. Any correlation is simply the result of the common impact of the increasing influence of foreigners.
Some calculators will generate a best fit line. Be careful. In algebra straight lines had the form y = mx + b where m was the slope and b was the y-intercept. In statistics lines are described using the equation y = a + bx. Thus b is the slope! And a is the y-intercept! You would not need to know this but your calculator will likely use b for the slope and a for the y-intercept. The exception is some TI calculators that use SLP and INT for slope and intercept respectively.
Note only for those in physical science courses. In some physical systems the data point (0,0) is the most accurately known measurement in a system. In this situation the physicist may choose to force the linear regression through the origin at (0,0). This forces the line to have an intercept of zero. There is another function in spreadsheets which can force the intercept to be zero, the LINear ESTimator function. The following functions use time versus distance, common x and y values in physical science.
=LINEST(distance (y) values,time (x) values,0)
Note that the same as the slope and intercept functions, the y-values are entered first, the x-values are entered second.
A probability is the likelihood of an event or outcome. Probabilities are specified mathematically by a number between 0 and 1 including 0 or 1.
We use the notation P(eventLabel) = probability to report a probability.
There are three ways to assign probabilities.
Intuition/subjective measure. An educated best guess. Using available information to make a best estimate of a probability. Could be anything from a wild guess to an educated and informed estimate by experts in the field.
Equally Likely Events: Probabilities from mathematical formulas
In the following the word "event" and the word "outcome" are taken to have the same meaning.
The study of problems with equally likely outcomes is termed the study of probabilities. This is the realm of the mathematics of probability. Using the mathematics of probability, the outcomes can be determined ahead of time. Mathematical formulas determine the probability of a particular outcome. All measures are population parameters. The mathematics of probability determines the probabilities for coin tosses, dice, cards, lotteries, bingo, and other games of chance.
This course focuses not on probability but rather on statistics. In statistics, measurement are made on a sample taken from the population and used to estimate the population's parameters. All possible outcomes are not usually known. is usually not known and might not be knowable. Relative frequencies will be used to estimate population parameters.
Where each and every event is equally likely, the probability of an event occurring can be determined from
probability = ways to get the desired event/total possible events
or
probability = ways to get the particular outcome/total possible outcomes
P(head on a penny) = one way to get a head/two sides = 1/2 = 0.5 or 50%
That probability, 0.5, is the probability of getting a heads or tails prior to the toss. Once the toss is done, the coin is either a head or a tail, 1 or 0, all or nothing. There is no 0.5 probability anymore.
Over any ten tosses there is no guarantee of five heads and five tails: probability does not work like that. Over any small sample the ratios of expected outcomes can differ from the mathematically calculated ratios.
Over thousands of tosses, however, the ratio of outcomes such as the number of heads to the number of tails, will approach the mathematically predicted amount. We refer to this as the law of large numbers.
In effect, a few tosses is a sample from a population that consists, theoretically, of an infinite number of tosses. Thus we can speak about a population mean μ for an infinite number of tosses. That population mean μ is the mathematically predicted probability.
Population mean μ = (number of ways to get a desired outcome)/(total possible outcomes)
A six-sided die. Six sides. Each side equally likely to appear. Six total possible outcomes. Only one way to roll a one: the side with a single pip must face up. 1 way to get a one/6 possible outcomes = 0.1667 or 17%
P(1) = 0.17
The formula remains the same: the number of possible ways to get a particular roll divided by the number of possible outcomes (that is, the number of sides!).
Think about this: what would a three sided die look like? How about a two-sided die? What about a one sided die? What shape would that be? Is there such a thing?
Ways to get a five on two dice: 1 + 4 = 5, 2 + 3 = 5, 3 + 2 = 5, 4 + 1 = 5 (each die is unique). Four ways to get/36 total possibilities = 4/36 = 0.11 or 11%
Homework:
The sample space set of all possible outcomes in an experiment or system.
Bear in mind that the following is an oversimplification of the complex biogenetics of achromatopsia for the sake of a statistics example. Achromatopsia is controlled by a pair of genes, one from the mother and one from the father. A child is born an achromat when the child inherits a recessive gene from both the mother and father.
A is the dominant gene
a is the recessive gene
A person with the combination AA is "double dominant" and has
"normal" vision.
A person with the combination Aa is termed a carrier and has "normal" vision.
A person with the combination aa has achromatopsia.
Suppose two carriers, Aa, marry and have children. The sample space for this situation is as follows:
| mother | |||
| father | \ | A | a |
|---|---|---|---|
| A | AA | Aa | |
| a | Aa | aa | |
The above diagram of all four possible outcomes represents the sample space for this exercise. Note that for each and every child there is only one possible outcome. The outcomes are said to be mutually exclusive and independent. Each outcome is as likely as any other individual outcome. All possible outcomes can be calculated. the sample space is completely known. Therefore the above involves probability and not statistics.
The probability of these two parents bearing a child with achromatopsia is:
P(achromat) = one way for the child to inherit aa/four possible combinations = 1/4 = 0.25 or 25%
This does NOT mean one in every four children will necessarily be an achromat. Suppose they have eight children. While it could turn out that exactly two children (25%) would have achromatopsia, other likely results are a single child with achromatopsia or three children with achromatopsia. Less likely, but possible, would be results of no achromat children or four achromat children. If we decide to work from actual results and build a frequency table, then we would be dealing with statistics.
The probability of bearing a carrier is:
P(carrier) = two ways for the child to inherit Aa/four possible combinations = 2/4 = 0.50
Note that while each outcome is equally likely, there are TWO ways to get a carrier, which results in a 50% probability of a child being a carrier.
At your desk: mate an achromat aa father and carrier mother Aa.
Homework: Mate a AA father and an achromat aa mother.
See: http://www.achromat.org/ for more information on achromatopsia.
Genetically linked schizophrenia is another genetic example:
Mol Psychiatry. 2003 Jul;8(7):695-705, 643. Genome-wide scan in a large complex pedigree with predominantly male schizophrenics from the island of Kosrae: evidence for linkage to chromosome 2q. Wijsman EM, Rosenthal EA, Hall D, Blundell ML, Sobin C, Heath SC, Williams R, Brownstein MJ, Gogos JA, Karayiorgou M. Division of Medical Genetics, Department of Medicine, University of Washington, Seattle, WA, USA. It is widely accepted that founder populations hold promise for mapping loci for complex traits. However, the outcome of these mapping efforts will most likely depend on the individual demographic characteristics and historical circumstances surrounding the founding of a given genetic isolate. The 'ideal' features of a founder population are currently unknown. The Micronesian islandic population of Kosrae, one of the four islands comprising the Federated States of Micronesia (FSM), was founded by a small number of settlers and went through a secondary genetic 'bottleneck' in the mid-19th century. The potential for reduced etiological (genetic and environmental) heterogeneity, as well as the opportunity to ascertain extended and statistically powerful pedigrees makes the Kosraean population attractive for mapping schizophrenia susceptibility genes. Our exhaustive case ascertainment from this islandic population identified 32 patients who met DSM-IV criteria for schizophrenia or schizoaffective disorder. Three of these were siblings in one nuclear family, and 27 were from a single large and complex schizophrenia kindred that includes a total of 251 individuals. One of the most startling findings in our ascertained sample was the great difference in male and female disease rates. A genome-wide scan provided initial suggestive evidence for linkage to markers on chromosomes 1, 2, 3, 7, 13, 15, 19, and X. Follow-up multipoint analyses gave additional support for a region on 2q37 that includes a schizophrenia locus previously identified in another small genetic isolate, with a well-established recent genealogical history and a small number of founders, located on the eastern border of Finland. In addition to providing further support for a schizophrenia susceptibility locus at 2q37, our results highlight the analytic challenges associated with extremely large and complex pedigrees, as well as the limitations associated with genetic studies of complex traits in small islandic populations. PMID: 12874606 [PubMed - indexed for MEDLINE]
The above article is both fascinating and, at the same time, calls into question privacy issues. On the small island of Kosrae "three siblings from one nuclear family" are identifiable people.
Note to instructors: This book is unapologetically frequentist in its approach. Hard core long term frequency is the probability of an event. The author is keenly aware of the Bayesian objection to this definition and approach to statistics. This is an introductory first statistics course for students who have not studied any statistics prior to this class. The intent is to bring them up to speed in frequentist statistics leading in confidence intervals and two-tailed hypothesis testing and then have them use these tools in data exploration exercises. This text deliberately synonymizes relative frequency with probability. For deeper dive into the Bayesian approach and the issue with frequentist approaches, have a look at Bernoulli's Fallacy: Statistical Illogic and the Crisis of Modern Science by Aubrey Clayton and published by the Columbia University Press, 2021.
The third way to assign probabilities is from relative frequencies. Each relative frequency represents a probability of that event occurring for that sample space. Body fat percentage data was gathered from 58 females here at the College since summer 2001. The data had the following characteristics:
| count | 59 |
|---|---|
| mean | 28.7 |
| sx | 7.1 |
| min | 15.6 |
| max | 50.1 |
A five class frequency and relative frequency table has the following results:
BFI = Body Fat Index (percentage*100)
CLL = Class (bin) Lower Limit
CUL = Class (bin) Upper Limit (Excel uses)
Note that the classes are not equal width in this example.
| Medical Category | BFI fem CUL x |
Frequency f | Relative Frequency f/n or P(x) |
|---|---|---|---|
| Athletically fit* | 20 | 3 | 0.05 |
| Physically fit | 24 | 15 | 0.25 |
| Acceptable | 31 | 24 | 0.41 |
| Borderline obese (overfat) | 39 | 12 | 0.20 |
| Medically obese | 51 | 5 | 0.08 |
| Sample size n: | 59 | 1.00 |
* body fat percentage category
This means there is a...
The most probable result (most likely) is a body fat measurement between 24.1 and 31 with a 41% probability of a student being in each of either of these intervals.
Remember that...
The sum of the frequencies is the sample size.
The sum of the relative frequencies is always one: probabilities add to one, which is also 100%.
The sum of the frequencies being the sample size and the sum of the relative frequencies were ways to check the accuracy of the frequency table.
The same table, but for male students:
| Medical Category | BFI male CUL x |
Frequency f |
Relative Frequency f/n or P(x) |
|---|---|---|---|
| Athletically fit* | 13 | 9 | 0.18 |
| Physically fit | 17 | 11 | 0.22 |
| Acceptable | 20 | 10 | 0.20 |
| Borderline obese (overfat) | 25 | 9 | 0.18 |
| Medically obese | 50 | 12 | 0.24 |
Sample size n: |
51 | 1.00 |
The male students have a higher probability of being obese than the female students!
What is the probability that a Kosraean lives outside of Kosrae? An informal survey done on the 25th of December 2007 produced the following data. The table also includes data gathered Christmas 2003.
Kosraean population estimates
| Location | 2003 Conservative | 2003 Possible | 2007 | Growth |
|---|---|---|---|---|
| Ebeye | - | - | 30 | - |
| Guam | 200 | 300 | 300 | 50% |
| Honolulu | 600 | 1000 | 1000 | 67% |
| Kona | 200 | 200 | 800 | 300% |
| Maui | 100 | 100 | 60 | -40% |
| Pohnpei | 200 | 200 | 300 | 50% |
| Seattle | 200 | 200 | 600 | 200% |
| Texas | 200 | 200 | N/A | - |
| Virgina Beach | 200 | 200 | N/A | - |
| USA Other | - | 200 | N/A | - |
| Diaspora sums: | 1700 | 2400 | 3090 | - |
| Kosrae | 7663 | 7663 | 8183 | - |
| Est. Total Pop.: | 9363 | 10063 | 11273 | - |
| Percentage abroad: | 18.2% | 23.8% | 27% | 48% |
The relative frequency of 27% is a point estimate for the probability that a Kosraean lives outside of Kosrae.
For relative frequency probability calculations, as the sample size increases the probabilities get closer and closer to the true population parameter (the actual probability for the population). Bigger samples are more accurate.
Inferential statistics is all about measuring a sample and then using those values to predict the values for a population. The measurements of the sample are called statistics, the measurements of the population are called parameters. Some sample statistics are good predictors of their corresponding population parameter. Other sample statistics are not able to predict their population parameter. The sample must be a good, representative sample of the population. If the sample is not properly chosen, then no predictions can be made.
The sample size will always be smaller than the population. The population size N cannot be predicted from the sample size n. The sample mode is not usually the same as the population mode. The sample median can predict the population median. This text does not further explore inference of population medians from sample medians. If a sample is normally distributed, then the sample mean is a more efficient estimator of the population mean than the median.
The sample mean for a good, random sample, is a reasonable point estimate of the population mean μ. The sample standard deviation sx predicts the population standard deviation σ. The shape of the distribution of the sample is a good predictor of the shape of the distribution of the population.
That the shape of the population distribution can be predicted by the shape of the distribution of a good random sample is important. Later in the course we will be predicting the population mean μ. Instead of predicting a single value we will predict a range in which the population mean will likely be found.
Consider as an example the following question, "How long does it take to drive from Kolonia to the national campus on Pohnpei?" A typical answer would be "Ten to twenty minutes." Everyone knows that the time varies, so a range is quoted. The average time to drive to the national campus is somewhere in that range.
Determining the appropriate range in which a population mean will be found depends on the shape of the distribution. A bimodal distribution is likely to need a larger range than a symmetrical bell shaped distribution in order to be sure to capture the population mean.
As a result of the above, we need to understand the shape of distributions generated by different systems. The most important shape in statistics is the shape of a purely random distribution, like that generated by tossing many pennies.
In class exercise: flipping seven pennies. Student flip seven pennies and record the number of heads. The data for a section is gathered and tabulated. The students then prepare a relative frequency histogram of the number of heads and calculate the mean number of heads from Σ x*p(x).
In the table below, seven pennies are tossed eight hundred and fifty eight times. For each toss of the seven pennies, the number of pennies landing heads up are counted.
| # of heads x | Frequency | Rel Freq P(x) |
|---|---|---|
| 7 | 9 | 0.0105 |
| 6 | 112 | 0.1305 |
| 5 | 147 | 0.1713 |
| 4 | 228 | 0.2657 |
| 3 | 195 | 0.2273 |
| 2 | 120 | 0.1399 |
| 1 | 45 | 0.0524 |
| 0 | 2 | 0.0023 |
| 858 | 1.00 |
The relative frequency histogram for a large number of pennies is usually a heap-like shape. For seven pennies the theoretic shape of an infinite number of tosses can be calculated by considering the whole sample space for seven pennies
HHHHHHH HHHHHHT HHHHHHTT HHHHTTT HHHTTTT HHTTTTTT HTTTTTT TTTTTTT
....... HHHHHTH HHHHHTHT HHHTHTT HHTHTTT THTTTTTH TTTTTTH
....... HHHHTHH HHHHTHHT HHTHHTT HTHHTTT THTTTTHT TTTTTHT
....... ... ... ... ... ... ...
If one works out all the possible combinations then one attains:
(two sides)^(7 pennies) = 128 total possibilities
1 way to get seven heads/128 total possible outcomes = 1/128= 0.0078
7 ways to get six heads and one tail/128 possibilities = 7/128 =0.0547
21 ways to get five heads and two tails/128 = 21/128 = 0.1641
35 ways to get four heads and three tails/128 = 35/128 = 0.2734
35 ways to get three heads and four tails/128 = 35/128 = 0.2734
21 ways to get two heads and five tails/128 = 21/128 = 0.1641
7 ways to get one head and six tails/128 possibilities = 7/128 =0.0547
1 way to get seven tails/128 total possible outcomes = 1/128= 0.0078
If the theoretic relative frequencies (probabilities) are added to our table:
| # of heads x | Frequency | Rel Freq P(x) | Theoretic |
|---|---|---|---|
| 7 | 9 | 0.0105 | 0.0078 |
| 6 | 112 | 0.1305 | 0.0547 |
| 5 | 147 | 0.1713 | 0.1641 |
| 4 | 228 | 0.2657 | 0.2734 |
| 3 | 195 | 0.2273 | 0.2734 |
| 2 | 120 | 0.1399 | 0.1641 |
| 1 | 45 | 0.0524 | 0.0547 |
| 0 | 2 | 0.0023 | 0.0078 |
| 858 | 1.00 | 1.00 |
If the theoretic relative frequencies are added as a line to our graph, the following graph results:
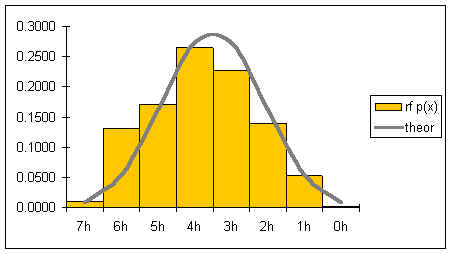
The gray line represents the shape of the distribution for an infinite number of coin tosses. The shape of the distribution is symmetrical.
If both the number of pennies is increased as well as the number of tosses, then the graph would become smoother and increasingly symmetrical. Below is a graph for tens of thousands of tosses of 21 pennies.
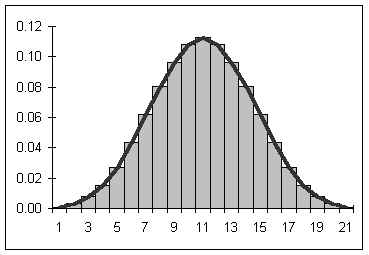
The shape of the smooth curve is called the "normal distribution" in statistics.
As noted in earlier chapters, statistics are the measures of a sample. The measures are used to characterize the sample and to infer measures of the population termed parameters.
A parameter is a numerical description of a population. Examples include the population mean μ and the population standard deviation σ.
A statistic is a numerical description of a sample. Examples include a sample mean x and the sample standard deviation sx.
Good samples are random samples where any member of the population is equally likely to be selected and any sample of any size n is equally likely to be selected. Consider four samples selected from a population. The samples need not be mutually exclusive as shown, they may include elements of other samples.
The sample means x1, x2, x3, x4, can include a smallest sample mean and a largest sample mean. Choosing a number of classes can generate a histogram for the sample means. The question this chapter answers is whether the shape of the distribution of sample means from a population is any shape or a specific shape.
The shape of the distribution of the sample mean is not any possible shape. The shape of the distribution of the sample mean, at least for good random samples with a sample size larger than 30, is a normal distribution. That is, if you take random samples of 30 or more elements from a population, calculate the sample mean, and then create a relative frequency distribution for the means, the resulting distribution will be normal.
In the following diagram the underlying data is bimodal and is depicted by the columns with thin outlines. Thirty data elements were sampled forty times and forty sample means were calculated. A relative frequency histogram of the sample means is plotted with a heavy black outline. Note that though the underlying distribution is bimodal, the distribution of the forty means is heaped and close to symmetrical. The distribution of the forty sample means is normal.
The center of the distribution of the sample means is, theoretically, the population mean. To put this another simpler way, the average of the sample averages is the population mean. Actually, the average of the sample averages approaches the population mean as the number of sample averages approaches infinity.
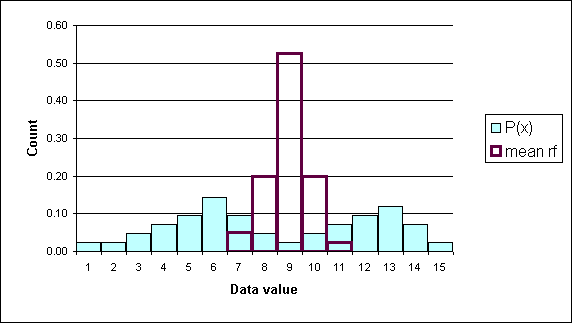
The sample mean distribution is a heap shaped, as in the shape of the normal distribution, and centered on the population mean.
If the sample size is 30 or more, then the sample means are NORMALLY distributed even when the underlying data is NOT normally distributed! If the sample size is less than 30, then the distribution of the samples means is normal if and only if the underlying data is normally distributed.
The normal distribution of the sample means (averages) allows us to use our normal distribution probabilities to estimate a range for μ. The mean of the sample means is a point estimate for the population mean μ.
The mean of the sample means can be written as:
![]()
In this text the above is sometimes written as μ x
The value of the mean of the sample means μ x is, for a very large number of samples each of which has a very large sample size, the population mean. As a practical matter we use the mean of a single large sample. How large? The sample size must be at least n = 30 in order for the sample mean (a statistic) to be a good estimate for the population mean (a parameter). This requirement is necessary to ensure that the distribution of the sample means will be normal even when the underlying data is not normal. If we are certain the data is normally distributed, then a sample size n of less than 30 is acceptable.
Later in the course we will modify the normal distribution to handle samples of sizes less than 30 for which the distribution of the underlying data is either unknown or not normal. This modification will be called the student's t-distribution. The student's t-distribution is also heap-shaped.
The normal distribution, and later the student's t-distribution, will be used to quote a range of possible values for a population mean based on a single sample mean. Knowing that the sample mean comes from a heap-shaped distribution of all possible means, we will center the normal distribution at the sample mean and then use the area under the curve to estimate the probability (confidence) that we have "captured" the population mean in that range.
The Law of Large Numbers says that as the sample size n increases, the sample mean x gets ever closer the population mean μ. If a distribution has a mean μ and a standard deviation σ, as the sample sizes grow larger, the Central Limit Theorem says that the values of the sample means will tend to be distributed increasingly like the normal distribution. (With thanks to Dr. Lewis E. MacCarter for clarifying this distinction, personal correspondence).
The standard deviation of the distribution of the sample means
There is one complication: the sample standard deviation of a single sample is not a good estimate of the standard deviation of the sample means. Note that the distribution of the sample means is NARROWER than the sample in the above example. The shape of the distribution of the sample means is narrower and taller than the shape of the underlying data. In the diagram, the shape of the underlying data is normal, the taller narrower distribution is the distribution of all the sample means for all possible samples.
The standard deviation of a single sample has to be reduced to reflect this. This reduction turns out to be inversely related to the square root of the sample size. This is not proven here in this text.
The standard deviation of the distribution of the sample means is equal to the actual population standard deviation divided by the square root of n.
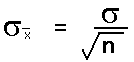
The standard deviation divided by the square root of the sample size is called the standard error of the mean.
If σ is known, then the above formula can be used and the distribution of the sample mean is normal.
As a practical matter, since we rarely know the population standard deviation σ, we will use the sample standard deviation sx in class to estimate the standard deviation of the sample means. This formula will then appear in various permutations in formulas used to estimate a population mean from a sample mean. When we use the sample standard deviation sx we will use the student's t-distribution. The student's t-distribution looks like a normal distribution. The student's t-distribution, however, is adjusted to be a more accurate predictor of the range for a population mean. Later we will learn to use the student's t-distribution. Until that time we will play a little fast and loose and use sample standard deviations to calculate the standard error of the mean.
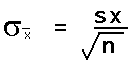
In a spreadsheet the standard error of the mean can be calculated using the formula:
=STDEV(data)/SQRT(COUNT(data))
Another way to think about the standard error is that the standard errors captures the "fuzziness" of the mean. The mean is different than individual data points, individual numbers. The mean is composed of a collection of data values. The mean is composed of a sample of data values. Pick a different sample from the population, you get a different mean. The change in the mean is only a random result. The change in the mean has no meaning. The standard error is a measure of that fuzziness. In the next chapter that "fuzziness" will be expanded to two standard errors to either side of the mean. Later that "two standard errors" will be adjusted for small sample sizes. Two standard errors, and the subsequent adjustment to that value of two, are ways of mathematically describing the fuzziness of the mean.
Whenever we use a single statistic to estimate a parameter we refer to the estimate as a point estimate for that parameter. When we use a statistic to estimate a parameter, the verb used is "to infer." We infer the population parameter from the sample statistic.
Some population parameters cannot be inferred from the statistic. The population size N cannot be inferred from the sample size n. The population minimum, maximum, and range cannot be inferred from the sample minimum, maximum, and range. Populations are more likely to have single outliers than a smaller random sample.
The population mode usually cannot be inferred from a smaller random sample. There are special circumstances under which a sample mode might be a good estimate of a population mode, these circumstances are not covered in this class.
The sample median can be a good point estimate for a population median, especially in situations where the data is not normally distributed. In a distribution with extreme outliers, the median is usually a better choice as an estimator than the mean. This text does not explore these distributions.
The statistic we will focus on is the sample mean x. The normal distribution of sample means for many samples taken from a population provides a mathematical way to calculate a range in which we expect to "capture" the population mean and to state the level of confidence we have in that range's ability to capture the population mean µ.
The sample mean x is a point estimate for the population mean µ
The sample mean x for a random sample will not be the exact same value as the true population mean µ.
The error of a point estimate is the magnitude of the point estimate minus the actual parameter (where the magnitude is always positive). The error in using x for µ is ( x − µ ). Note that to take a positive value we need to use either the absolute value |( x - µ )| or √( x - µ )2.
Note that the error of an estimate is the distance of the statistic from the parameter.
Unfortunately we cannot calculate the error. The reason why we are using the sample mean x to estimate the population mean µ is because we do not know the population mean µ.
For example, given the mean body fat index (BFI) of 51 male students at the national campus is x = 19.9 with a sample standard deviation of sx = 7.7, what is the error |( x - µ )| if µ is the average BFI for male COMFSM students?
We cannot calculate this. We do not know µ! So we say x is a point estimate for µ. That would make the error equal to √(x − x)2 = zero. This is a silly and meaningless answer.
Is x really the exact value of µ for all the males at the national campus? No, the sample mean is not going to be the same as the true population mean.
The sample standard deviation sx is a reasonable point estimate for the population standard deviation σ. In more advanced statistics classes concern over bias in the sample standard deviation as an estimator for the population standard deviation is considered more carefully. In this class, and in many applications of statistics, the sample standard deviation sx is used as the point estimate for the population standard deviation σ.
We might be more accurate if we were to say that the mean µ is somewhere between two values. We could estimate a range for the population mean µ by going one standard error below the sample mean and one standard error above the sample mean. Remember, the standard error is the σ/√(n). Note that the formula for the standard error requires knowing the population standard deviation σ. We do not usually know this value. In fact, if we knew σ then we would probably also know the population mean µ. In section 9.2 we will use the sample standard deviation or sx/√(n) and the student's t-distribution to calculate a range in which we expect to find the population mean µ.

In the diagram the lower curve represents the distribution of data in a population with a normal distribution. Remember, distribution simply means the shape of the frequency or relative frequency histogram, now charted as a continuous line. The narrower and taller line is the distribution of all possible sample means from that population.
For the population curve (lower, broader) the distance to each inflection point is one standard deviation: ± σ. For the distribution of the sample means (higher, narrower) the distance to each inflection point is one standard error of the mean: ± σ/√(n).
The area from minus one standard error to plus one standard error for the normal distribution is known to be 68.2%.
Here is a key point: If I set my estimate for µ to be between x - σ/√n and x + σ/√n, then there is a 0.682 probability that µ will be included in that interval.
The "68.2% probability" is termed "the level of confidence."
Probability note: the reality is that the population mean is either inside or outside the range we have calculated. We are right or wrong, 100% or 0%. Thus saying that there is a 68.2% probability that the population mean has been "captured" by the range is not actually correct. This is the main reason why we shift to calling the range for the mean a confidence interval. We start saying things such as "I am 68.2 percent confident the mean is in the range quoted." Statisticians assert that over the course of a lifetime, if one always uses a 68.2% confidence interval one will right 68.2% of the time in life. This is small comfort when an individual experimental result might be very important to you.
In many fields of inquiry a common level of confidence used is a 95% level of confidence. For the purposes of this course a 95% confidence interval is often used.
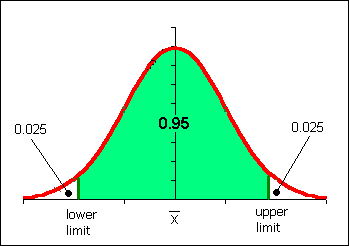
Note that when a confidence interval is not 95%, then specific reference to the chosen confidence level must be stated. Stating the level of confidence is always good form. While many studies are done at a 95% level of confidence, in some fields higher or lower levels of confidence may be common. Scientific studies often use 99% or higher levels of confidence.
When using the sample standard deviation sx to generate a confidence interval for the population mean, a distribution called the Student's t-distribution is used. The Student's t-distribution looks like the normal distribution, but the t-distribution changes shape slightly as the sample size n changes. The t-distribution looks like a normal distribution, but the shape "flattens" as n decreases. As the sample size decreases, the t-distribution becomes flatter and wider, spreading out the confidence interval and "pushing" the lower and upper limits away from the center. For n > 30 the Student's t-distribution is almost identical to the normal distribution. When we sketch the Student's t-distribution we draw the same heap shape with two inflection points.
To use the Student's t-distribution the sample must be a good, random sample. The sample size can be as small as n = 5. For n ≤ 10 the t-distribution will generate very large ranges for the population mean. The range can be so large that the estimate is without useful meaning. A basic rule in statistics is "the bigger the sample size, the better."
The spreadsheet function used to find limits from the Student's t-distribution does not calculate the lower and upper limits directly. The function calculates a value called "t-critical" which is written as tc. By using a range that is t-critical * standard error above and below the sample we can calculate the confidence interval in which we would expect to find the population mean to a level of confidence c.
The confidence interval will be:
x - tc*sx/√n ≤ µ ≤ x + tc*sx/√n
Some texts use t-critical multiplied by the Standard Error of the mean SE to generate the margin of error for the mean E. This calculation is not strictly necessary. If the margin of error is called for, then do not confuse the standard error of the mean with the margin of error for the mean. The Standard Error of the mean is sx/√(n). The Margin of Error for the mean (E) is the distance from either end of the confidence interval to the middle of the confidence interval. The margin of error is produced from the Standard Error:
Margin of Error for the mean = tc*standard error of the mean
Margin of Error for the mean = tc*sx/√n
In texts that use the margin of error for the mean the notation for the confidence interval is:
x - E ≤ µ ≤ x + E
The t-critical value will be calculated using the spreadsheet function TINV. TINV uses the area in the tails to calculate t-critical. The area under the whole curve is 100%, so the area in the tails is 100% − confidence level c. Remember that in decimal notation 100% is just 1. If the confidence level c is in decimal form use the spreadsheet function below to calculate tc:
=TINV(1−c,n−1)
If the confidence level c is entered as a percentage with the percent sign, then make sure the 1 is written as 100%:
=TINV(100%−c%,n−1)
The TINV function adjusts t-critical for the sample size n. The formula uses n − 1. This n − 1 is termed the "degrees of freedom." For confidence intervals of one variable the degrees of freedom are n − 1.
In Google Sheets™ the candlestick chart type can be used to make a confidence interval chart. Note that the mean is repeated twice, shrinking the center box of the candlestick chart to a line representing the mean value. In the Chart types tab of the Chart editor one may need to Switch rows/columns and adjust the Column header and Row label settings.
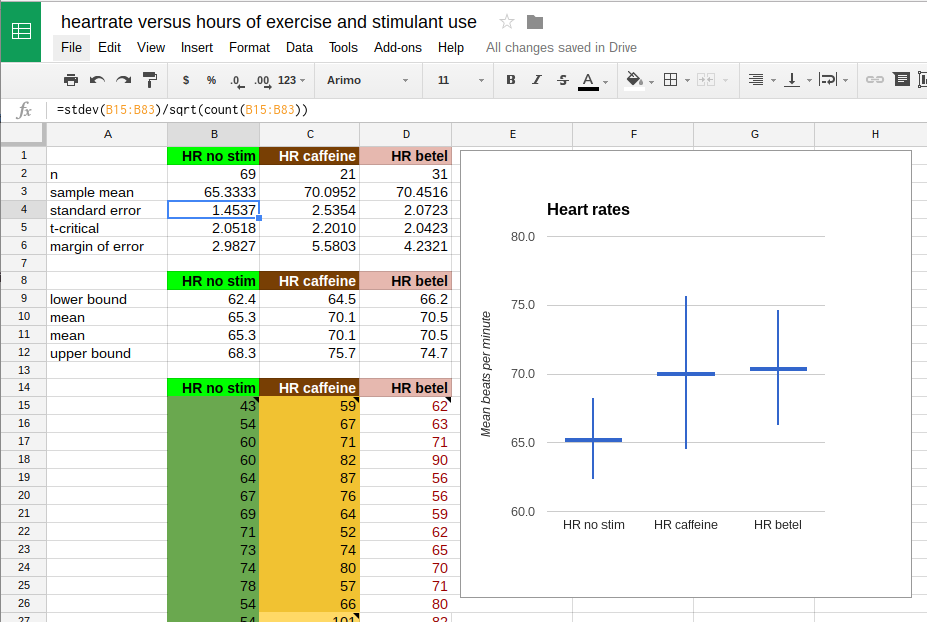
Google and the Google logo are registered trademarks of Google Inc., used with permission.
The confidence interval candlestick chart spreadsheet used to produce the above images with corrected and updated values in Google Sheets™
Runners run at a very regular and consistent pace. As a result, over a fixed distance a runner should be able to repeat their time consistently. While individual times over a given distance will vary slightly, the long term average should remain approximately the same. The average should remain within the 95% confidence interval.
For a sample size of n = 10 runs from the college in Palikir to Kolonia town, a runner has a sample mean x time of 61 minutes with a sample standard deviation sx of 7 minutes. Construct a 95% confidence interval for my population mean run time.
Step 1: Determine the basic sample statistics
sample size n = 10
sample mean x = 61
[61 is also the point est. for the pop. mean µ]
sample standard deviation sx = 7
Step 2: Calculate degrees of freedom, tc, standard error SE
degrees of freedom = 10 - 1 = 9
tc =TINV(1-0.95,10-1) = 2.2622
Standard Error of the mean sx/√n = 7/sqrt(10) = 2.2136
Keeping four decimal places in intermediate calculations can help reduce rounding errors in calculations. Alternatively use a spreadsheet and cell references for all calculations.
Step 3: Determine margin of error E
Margin of error E for the mean
= tc*sx/√n = 2.2622*7/√10 = 5.01
Given that: x - E ≤ µ ≤ x + E, we can substitute the values for x and E to obtain the 95% confidence interval for the population mean µ:
Step 4: Calculate the confidence interval for the mean
61 − 5.01 ≤ µ ≤ 61 + 5.01
55.99 ≤ µ ≤ 66.01
I can be 95% confident that my population mean µ run time should be between 56 and 66 minutes.
| Jumps | ||||||||
|---|---|---|---|---|---|---|---|---|
| 102 | 66 | 42 | 22 | 24 | 107 | 8 | 26 | 111 |
| 79 | 61 | 45 | 43 | 10 | 17 | 20 | 45 | 105 |
| 68 | 69 | 79 | 13 | 11 | 34 | 58 | 40 | 213 |
On Thursday 08 November 2007 a jump rope contest was held at a local elementary school festival. Contestants jumped with their feet together, a double-foot jump. The data seen in the table is the number of jumps for twenty-seven female jumpers. Calculate a 95% confidence interval for the population mean number of jumps.
The sample mean x for the data is 56.22 with a sample standard deviation of 44.65. The sample size n is 27. You should try to make these calculations yourself. With those three numbers we can proceed to calculate the 95% confidence interval for the population mean µ:
Step 1: Determine the basic sample statistics
sample size n = 27
sample mean x = 56.22
sample standard deviation sx = 44.65
Step 2: Calculate degrees of freedom, tc, standard error SE
The degrees of freedom are n − 1 = 26
Therefore tcritical = TINV(1-0.95,27-1) = 2.0555
The Standard Error of the mean SE = sx/√27 = 8.5924
Step 3: Determine margin of error E
Therefore the Margin of error for the mean E
tc* SE = 2.0555*8.5924 = 17.66
The 95% confidence interval for the mean is x − E ≤ µ ≤ x + E
Step 4: Calculate the confidence interval for the mean
56.22 − 17.66 ≤ µ ≤ 56.22 + 17.66
38.56 ≤ µ ≤ 73.88
The population mean for the jump rope jumpers is estimated to be between 38.56 and 73.88 jumps.
In 2003 a staffer at the Marshall Islands department of education noted in a newspaper article that Marshall's Island public school system was not the weakest in Micronesia. The staffer noted that Marshall's was second weakest, commenting that education metrics in the Marshall's outperform those in Chuuk's public schools.
In 2004 fifty students at Marshall Islands High School took the entrance test. Ten students Achieved admission to regular college programs. In Chuuk state 7% of the public high school students gain admission to the regular college programs. If the 95% confidence interval for the Marshall Islands proportion includes 7%, then the Marshallese students are not academically more capable than the Chuukese students, not statistically significantly so. If the 95% confidence interval does not include 7%, then the Marshallese students are statistically significantly stronger in their admissions rate.
Finding the 95% confidence interval for a proportion involves estimating the population proportion p. The fifty students at Marshall Islands High School are taken as a sample. The proportion who gained admission, 10/50 or 20%, is the sample proportion. The population proportion is treated as unknown, and the sample proportion is used as the point estimate for the population proportion.
Note: In this text the letter p is used for the sample proportion of successes instead of "p hat". A capital P is used to refer to the population proportion.
The letter n refers to the sample size. The letter p is the sample proportion of successes. The letter q is the sample proportion of failures. In the above example n is 50, p is 10/50 or 0.20, and q is 40/50 or 0.80
Estimating the population proportion P can only be done if the following conditions are met:
np > 5
nq > 5
In the example np = (50)(0.20) = 10 which is > 5. nq = (50)(0.80) = 40 which is also > 5
The standard error of a proportion is:
For the example above the standard error is:
=sqrt(0.2*0.8/50)
For the calculation of the confidence interval of a proportion, only the standard error calculation is new. The rest of the steps are the same as in the preceding section.
The standard error for the proportion is 0.0566. The margin of error E is then calculated in much the same way as in the section above, by multiplying tc by the standard error. tc is still found from the TINV function. The degrees of freedom will remain n-1.
The margin of error E is:
=TINV(1-0.95,50-1)*sqrt((0.2)*(0.8)/50)
The margin of error E is 0.1137
The confidence interval for the population proportion P is:
p − E ≤ P ≤ p + E
0.20 − 0.1137 ≤ P ≤ 0.20 + 0.1137
0.0863 ≤ P ≤ 0.3137
The result is that the expected population mean for Marshall Island High School is between 8.6% and 31.2%. The 95% confidence interval does not include the 7% rate of the Chuuk public high schools. While the college entrance test is not a measure of overall academic capability, there are few common measures that can be used across the two nations. The result does not contradict the staffer's assertion that MIHS outperformed the Chuuk public high schools. This lack of contradiction acts as support for the original statement that MIHS outperformed the public high schools of Chuuk in 2004.
Homework: In twelve sumo matches Hakuho bested Tochiazuma seven times. What is the 90% confidence interval for the population proportion of wins by Hakuho over Tochiazuma. Does the interval extend below 50%? A commentator noted that Tochiazuma is not evenly matched. If the interval includes 50%, however, then we cannot rule out the possibility that the two-win margin is random and that the rikishi (wrestlers) are indeed evenly matched.
Hakuho won that night, upping the ratio to 8 wins to 5 losses to Tochiazuma. Is Hakuho now statistically more likely to win or could they still be evenly matched at a confidence level of 90%?
Suppose you are designing a study and you have in mind a particular error E you do not want to exceed. You can determine the sample size n you'll need if you have prior knowledge of the standard deviation sx. How would you know the sample standard deviation in advance of the study? One way is to do a small "pre-study" to obtain an estimate of the standard deviation. These are often called "pilot studies."
If we have an estimate of the standard deviation, then we can estimate the sample size needed to obtain the desired error E.
Since E = tc*sx/√n, then solving for n yields = (tc*sx/E)²
Note that this is not a proper mathematical solution because tc is also dependent on n. While many texts use zc from the normal distribution in the formula, we have not learned to calculate zc.
In the "real world" what often happens is that a result is found to not be statistically significant as the result of an initial study. Statistical significance will be covered in more detail later. The researchers may have gotten "close" to statistical significance and wish to shrink the confidence interval by increasing the sample size. A larger sample size means a smaller standard error (n is in the denominator!) and this in turn yields a smaller margin of error E. The question is how big a sample would be needed to get a particular margin of error E.
The value for tc from pilot study can be used to estimate the new sample size n. The resulting sample size n will be slightly overestimated versus the traditional calculation made with the normal distribution. This overestimate, while slightly unorthodox, provides some assurance that the error E will indeed shrink as much as needed.
In a study of body fat for 51 males students a sample mean x of 19.9 with a standard deviation of 7.7 was measured. This led to a margin of error E of 2.17 and a confidence interval 17.73 ≤ µ ≤ 22.07
Suppose we want a margin of error E = 1.0 at a confidence level of 0.95 in this study of male student body fat. We can use the sx from the sample of 51 students to estimate my necessary sample size:
n = (2.0086*7.7/1)2 = 239.19 or 239 students. Thus I estimate that I will need 239 male students to reduce my margin of error E to ±1 in my body fat study.
Other texts which use zc would obtain the result of 227.77 or 228 students. The eleven additional students would provide assurance that the margin of error E does fall to 1.0.
That one can calculate a sample size n necessary to reduce a margin of error E to a particular level means that for any hypothesis test (chapter ten) in which the means have a mathematical difference, statistical significance can be eventually be attained by sufficiently increasing the sample size. This may sound appealing to the researcher trying to prove a difference exists, but philosophically it leaves open the concept that all things can be proven true for sufficiently large samples.
In this chapter we explore whether a sample has a sample mean x that could have come from a population with a known population mean μ. There are two possibilities. In Case I below, the sample mean x comes from the population with a known mean μ. In Case II, on the right, the sample mean x does not come from the population with a known mean μ. For our purposes the population mean μ could be a pre-existing mean, an expected mean, or a mean against which we intend to run the hypothesis test. In the next chapter we will consider how to handle comparing two samples to each other to see if they come from the same population.
In case I a sample taken from the population is likely to produce the sample mean seen for that particular sample. In case II a sample taken from the population is unlikely to produce the sample mean seen for that particular sample. Put another way, in case II the sample is not likely to have come from the population based on a significant difference between the sample mean and the population mean.
Suppose we want to do a study of whether the female students at the national campus gain body fat with age during their years at COM-FSM. Suppose we already know that the population mean body fat percentage for the new freshmen females 18 and 19 years old is μ = 25.4.
We measure a sample size n = 12 female students at the national campus who are 21 years old and older and determine that their sample mean body fat percentage is x = 30.5 percent with a sample standard deviation of sx = 8.7.
Can we conclude that the female students at the national campus gain body fat as they age during their years at the College?
Not necessarily. Samples taken from a population with a population mean of μ = 25.4 will not necessarily have a sample mean of 25.4. If we take many different samples from the population, the sample means will distribute normally about the population mean, but each individual mean is likely to be different than the population mean.
In other words, we have to consider what the likelihood of drawing a sample that is 30.5 - 25.4 = 5.1 units away from the population mean for a sample size of 12. If we knew more about the population distribution we would be able to determine the likelihood of a 12 element sample being drawn from the population with a sample mean 5.1 units away from the actual population mean.
In this case we know more about our sample and the distribution of the sample mean. The distribution of the sample mean follows the student's t-distribution. So we shift from centering the distribution on the population mean and center the distribution on the sample mean. Then we determine whether the confidence interval includes the population mean or not. We construct a confidence interval for the range of the population mean for the sample.
If this confidence interval includes the known population mean for the 18 to 19 years olds, then we cannot rule out the possibility that our 12 student sample is from that same population. In this instance we cannot conclude that the women gain body fat.
If the confidence interval does NOT include the known population mean for the 18 to 19 year old students then we can say that the older students come from a different population: a population with a higher population mean body fat. In this instance we can conclude that the older women have a different and probably higher body fat level.
One of the decisions we obviously have to make is the level of confidence we will use in the problem. Here we enter a contentious area. The level of confidence we choose, our level of bravery or temerity, will determine whether or not we conclude that the older females have a different body fat content. For a detailed if somewhat advanced discussion of this issue see The Fallacy of the Null-Hypothesis Significance Test by William Rozeboom.
In education and the social sciences there is a tradition of using a 95% confidence interval. In some fields three different confidence intervals are reported, typically a 90%, 95%, and 99% confidence interval. Why not use a 100% confidence interval? The normal and t-distributions are asymptotic to the x-axis. A 100% confidence interval would run to plus and minus infinity. We can never be 100% confident.
In the above example a 95% confidence interval would be calculated in the following way:
n = 12
x = 30.53
sx = 8.67
c = 0.95
degrees of freedom = 12 -1 = 11
tc = tinv((1-0.95,11) = 2.20
x - tc*8.67/√12 < μ <
x + tc*8.67/√12
25.02 < μ < 36.04
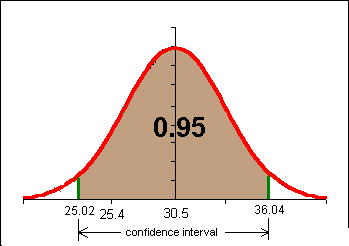
The 95% confidence interval for our n = 12 sample includes the population mean 25.3. We CANNOT conclude at the 95% confidence level that this sample DID NOT come from a population with a population mean μ of 25.3.
Another way of thinking of this is to say that 30.5 is not sufficiently separated from 25.8 for the difference to be statistically significant at a confidence level of 95% in the above example.
In common language, the women are not gaining body fat.
The above process is reduced to a formulaic structure in hypothesis testing. Hypothesis testing is the process of determining whether a confidence interval includes a previously known population mean value. If the population mean value is included, then we do not have a statistically significant result. If the mean is not encompassed by the confidence interval, then we have a statistically significant result to report.
Homework
If I expand my study of female students 21+ to n = 24 and find a sample mean x = 28.7 and an sx=7, is the new sample mean statistically significantly different from a population mean μ of 25.4 at a confidence level of c = 0.90?
In this section the language of hypothesis testing is introduced. A new statistic, the "t-statistic" is also introduced. In this text the choice is made to use two-tailed hypothesis tests. This retains the result found with a confidence interval hypothesis test found in the previous section. This also means that 1 - c = α and 1 - α = c. In hypothesis testing one sets up a binary choice between a hypothesis of no change and a hypothesis that there is a change.
The null hypothesis is the supposition that there is no change in a value from some pre-existing, historical, or expected value. The null hypothesis literally supposes that the change is null, non-existent, that there is no change.
In the previous example the null hypothesis would have been H0: μ = 25.4
The way to read that is to understand the μ as meaning "the sample could have a population mean of 25.4". This does not mean that the population mean IS 25.4, only that the sample could come from a population with a population mean of 25.4.
The alternate hypothesis is the supposition that there is a change in the value from some pre-existing, historical, or expected value. Note that the alternate hypothesis does NOT say the "new" value is the correct value, just that whatever the mean μ might be, it is not that given by the null hypothesis.
H1: μ ≠ 25.4
We run hypothesis test to determine if new data confirms or rejects the null hypothesis.
If the new data falls within the confidence interval, then the new data does not contradict the null hypothesis. In this instance we say that "we fail to reject the null hypothesis." Note that we do not actually affirm the null hypothesis. This is really little more than semantic shenanigans that statisticians use to protect their derrieres. Although we run around saying we failed to reject the null hypothesis, in practice it means we left the null hypothesis standing: we de facto accepted the null hypothesis.
If the new data falls outside the confidence interval, then the new data would cause us to reject the null hypothesis. In this instance we say "we reject the null hypothesis." Note that we never say that we accept the alternate hypothesis. Accepting the alternate hypothesis would be asserting that the population mean is the sample mean value. The test does not prove this, it only shows that the sample could not have the population mean given in the null hypothesis.
For two-tailed tests, the results are identical to a confidence interval test. Note that confidence interval never asserts the exact population mean, only the range of possible means. Hypothesis testing theory is built on confidence interval theory. The confidence interval does not prove a particular value for the population mean , so neither can hypothesis testing.
In our example above we failed to reject the null hypothesis H0 that the population mean for the older students was 25.4, the same population mean as the younger students.
In the example above a 95% confidence interval was used. At this point in your statistical development and this course you can think of this as a 5% chance we have reached the wrong conclusion.
Imagine that the 18 to 19 year old students had a body fat percentage of 24 in the previous example. We would have rejected the null hypothesis and said that the older students have a different and probably larger body fat percentage.
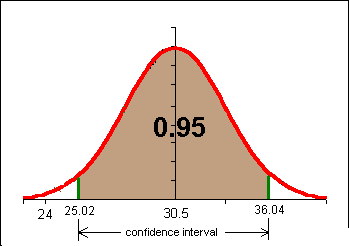
There is, however, a small probability (less than 5%) that a 12 element sample with a mean of 30.5 and a standard deviation of 8.7 could come from a population with a population mean of 24. This risk of rejecting the null hypothesis when we should not reject it is called alpha α. Alpha is 1-confidence level, or α = 1-c. In hypothesis testing we use α instead of the confidence level c.
| Suppose | And we fail to reject H0 | Reject H0 as false |
|---|---|---|
| H0 is true | Correct decision. Probability: 1 − α | Type I error. Probability: α |
| H0 is false | Type II error. Probability: β | Correct decision. Probability: 1 − β |
Hypothesis testing seeks to control alpha α. We cannot determine β (beta) with the statistical tools you learn in this course.
Alpha α is called the level of significance. 1 − β is called the "power" of the test.
The regions beyond the confidence interval are called the "tails" or critical regions of the test. In the above example there are two tails each with an area of 0.025. Alpha α = 0.05
A type I error, the risk of which is characterized by alpha α, is also known as a false positive. A type I error is finding that a change has happened, finding that a difference is significant, when it is not.
A type II error, the risk of which is characterized by beta β, is also known as a false negative. A type II error is the failure to find that a change has happened, finding that a difference is not significant, when it is.
If you increase the confidence level c, then alpha decreases and beta increases. High levels of confidence in a result, small alpha values, small risks of a type I error, leader to higher risks of committing a type II error. Thus in hypothesis testing there is a tendency to utilize an alpha of 0.05 or 0.01 as a way to controlling the risk of committing a type II error.
Another take on type I and type II errors:

Source information: Jim Thornton via Flowing Data
For hypothesis testing it is simply safest to always use the t-distribution. In the example further below we will run a two-tail test.
Steps
Put another way, if the absolute value of the t-statistic is larger than t-critical, then the result is statistically significant and we reject the null hypothesis.
If |t| > tc then reject the null hypothesis
If |t| < tc then fail to reject the null hypothesis
Calculating the t-statistic in a spreadsheet:
=(AVERAGE(data)-μ)/(STDEV(data)/SQRT(n))
where μ is the expected population mean.
Using the data from the first section of these notes:
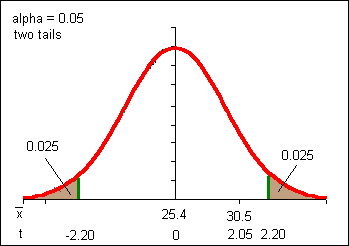
Note the changes in the above sketch from the confidence interval work. Now the distribution is centered on μ with the distribution curve described by a t-distribution with eleven degrees of freedom. In our confidence interval work we centered our t-distribution on the sample mean. The result is, however, the same due to the symmetry of the problems and the curve. If our distribution were not symmetric we could not perform this sleight of hand.
The hypothesis test process reduces decision making to the question, "Is the t-statistic t greater than the t-critical value tc? If t > tc, then we reject the null hypothesis. If t < tc, then we fail to reject the null hypothesis. Note that t and tc are irrational numbers and thus unlikely to ever be exactly equal.
When the absolute value of the t-statistic is less than t-critical:
When the absolute value of the t-statistic is more than t-critical:
A population of marbles has a population mean mass μ of 5.20 grams. A sample of five marbles was randomly selected from the population: 5.2, 4.9, 5.2, 5.7, and 5.9 grams. The sample mean x is 5.380 grams with a sample standard deviation of 0.409. At an alpha α = 0.05, could this sample of marbles have a population mean of 5.20 grams? A spreadsheet with data and a video for this example were posted online in 2020.
H0: μ = 5.20
H1: μ ≠ 5.20
Pay close attention to the above! We DO NOT write H1: μ = 5.380. This is perhaps a common beginning mistake. The null hypothesis is whether the population mean for the five run sample could be 5.20.
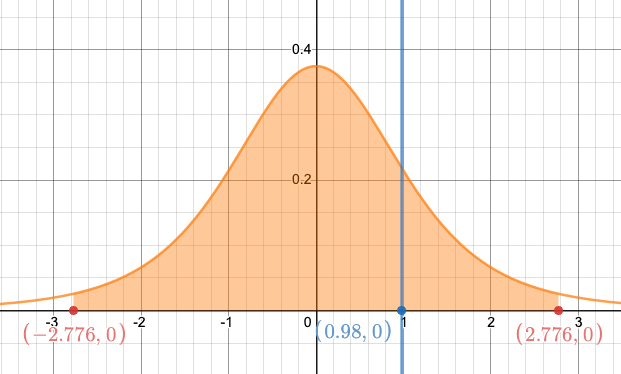
Note that in my sketch I am centering my distribution on the population mean and looking at the distribution of sample means for sample sizes of 5 based on that population mean. Then I look at where my actual sample mean falls with respect to that distribution.
Note too that my t-statistic t does not fall "beyond" the critical values. I do not have enough separation from my population mean: I cannot reject H0. So I fail to reject H0. The five marbles could have come from the population.
The p-value is a calculation of the area "beyond" the t-statistic. For two-tailed tests the area beyond the positive t-statistic and the area below the negative value of the t-statistic is considered.
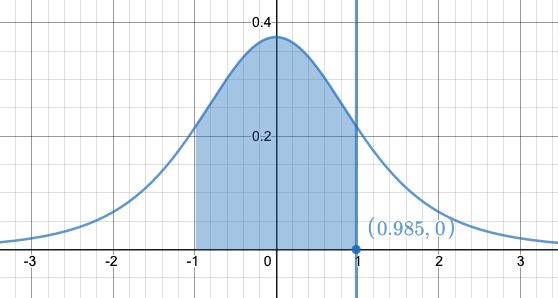
Shaded area = 0.620. Unshaded area = p-value = 0.380. Link
For the example in 10.2.2 the unshaded area under the curve and above the x-axis in the diagram is the p-value. If this unshaded area drops below alpha, which for us is 0.05, then we reject the null hypothesis. Thus the p-value is a third way to determine significance. Some functions that we will meet in the next chapter return only the p-value. And many studies often only cite p-values. To some extent, the p-value has been abused, and a definition of what exactly the p-value means is hard to put into words. Not even scientists can easily explain p-values.
In this text the p-value is treated as only informing one whether a result is "surprising" or not. In this text "surprising" is any p-value less than 0.05. If a result is surprising that means that the distance of the sample mean from the proposed population mean is surprisingly large, as in large enough to be statistically significant. Surprising means we reject the null hypothesis. If the p-value is larger than 0.05, the result is not surprising and we fail to reject the null hypothesis.
The p-value is calculated using the formula:
=TDIST(ABS(t),degrees of freedom,number of tails)
For a single variable sample and a two-tailed distribution, the spreadsheet equation becomes:
=TDIST(ABS(t),n−1,2)
The degrees of freedom are n − 1 for comparison of a sample mean to a known or pre-existing population mean μ.
Note that TDIST can only handle positive values for the t-statistic, hence the absolute value function. If you already have a positive t-statistic, the ABS function can be omitted from the formula.
When the p-value is "not surprising" (larger than our chosen alpha):
When the p-value is "surprising" (less than our chosen alpha):
For two-tailed hypothesis testing, 1 − p-value is the confidence interval for which the new value does not include the pre-existing population mean. Another way to say this is that 1 − p-value is the maximum confidence level c we can have that the difference (change) is significant. We usually look for a maximum confidence level c of 0.95 (95%) or higher. Again, the confidence level does not indicate the probability that we are right - on any one test we cannot know if we are right. This means that the p-value is not the probability that you are wrong. Perhaps best to think of the p-value as how surprised one should be.
The p-value is often misunderstood and misinterpreted. The p-value should be thought of as a measure of whether one should be surprised by a result. If the p-value is less than a pre-chosen alpha, usually 0.05, that would be a surprising result. If the p-value is greater than the pre-chosen alpha, usually 0.05, then that would NOT be a surprising result.
The p-value is also a much abused concept. In March 2016 the American Statistical Association issued the following six principles which which address misconceptions and misuse of the p- value, are the following:
American Statistical Association (ASA) statement on statistical significance and P-Values. See also Statisticians Found One Thing They Can Agree On: It’s Time To Stop Misusing P-Values and The mismeasure of scientific significance The full AMA manuscript is at The ASA's statement on p-values: context, process, and purpose.
The American Statistical Association settled on the following informal definition of the P-value, "Informally, a p-value is the probability under a specified statistical model that a statistical summary of the data (for example, the sample mean difference between two compared groups) would be equal to or more extreme than its observed value."
Returning to our earlier example in this text where the body fat percentage of 12 female students 21 years old and older was x = 30.53 with a standard deviation sx=8.67 was tested against a null hypothesis H0 that the population mean body fat for 18 to 19 year old students was μ = 25.4. We failed to reject the null hypothesis at an alpha of 0.05. What if we are willing to take a larger risk? What if we are willing to risk a type I error rate of 10%? This would be an alpha of 0.10.
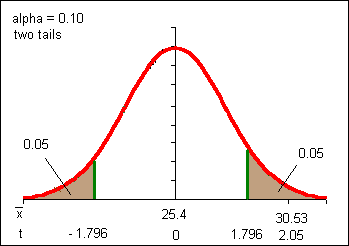
With an alpha of 0.10 (a confidence interval of 0.90) our results are statistically significant. These same results were NOT statistically significant at an alpha α of 0.05. So which is correct:
Note how we would have said this in confidence interval language:
The answer is that it depends on how much risk you are willing take, a 5% chance of committing a Type I error (rejecting a null hypothesis that is true) or a larger 10% chance of committing a Type I error. The result depends on your own personal level of adversity to risk. That is a heck of a mathematical mess: the answer depends on your personal willingness to take a particular risk.
Consider what happens if someone decides they only want to be wrong 1 in 15 times: that corresponds to an alpha of α = 0.067. They cannot use either of the above examples to decide whether to reject the null hypothesis. We need a way to indicate the boundary at which alpha changes from failure to reject the null hypothesis to rejection of the null hypothesis.
Citing the p-value gives us a way to provide that option. The p-value is also the smallest alpha for which we would still reject the null hypothesis. Suppose one is using alpha = 0.05. Then any p-value less than 0.05 leads to rejecting the null hypothesis. Suppose one chooses to use alpha = 0.10. Then any p-value less than this value leads to rejection. If the p-value is 0.08, then someone using an alpha of 0.05 does NOT reject the null while someone using 0.10 fails to reject the null hypothesis. For a p-value = 0.08 any alpha down to 0.08 leads to rejection of the null hypothesis while any alpha smaller than 0.08 leads to failure to reject the null hypothesis.
This sounds confusing and this can be confusing. The key point is that one has to choose one's alpha, one's willingness to risk a type I false positive error, before making any calculations. Another solution to this is to keep the same alpha that is consistently used in a particular field of study, often 0.05. With alpha at 0.05, then any p-value less than 0.05 is significant and leads to rejection of the null hypothesis.
For this body fat example the p-value = TDIST(ABS(2.05,11,2) = 0.06501
The p-value represents the SMALLEST alpha α for which the test is deemed "statistically significant" or, perhaps, "worthy of note."
The p-value is the SMALLEST alpha α for which we reject the null hypothesis.
Thus for all alpha greater than 0.065 we reject the null hypothesis. The "one in fifteen" person would reject the null hypothesis (0.0667 > 0.065). The alpha = 0.05 person would not reject the null hypothesis.
If the pre-chosen alpha is more than the p-value, then we reject the null hypothesis. If the pre-chosen alpha is less than the p-value, then we fail to reject the null hypothesis.
The p-value lets each person decide on their own level of risk and removes the arbitrariness of personal risk choices. This is also why alpha should be chosen before data is collected and analyzed. There is a risk of the statistical results influencing a decision on alpha if the choice is made after the analysis.
Because many studies in education and the social sciences are done at an alpha of 0.05, a p-value at or below 0.05 is used to reject the null hypothesis.
All of the work above in confidence intervals and hypothesis testing has been with two-tailed confidence intervals and two-tailed hypothesis tests. There are statisticians who feel one should never leave the realm of two-tailed intervals and tests.
Unfortunately, the practice by scientists, business, educators and many of the fields in social science, is to use one-tailed tests when one is fairly certain that the sample has changed in a particular direction. The effect of moving to a one tailed test is to increase one's risk of committing a Type I error.
One tailed tests, however, are popular with researchers because they increase the probability of rejecting the null hypothesis (which is what most researchers are hoping to do).
The complication is that starting with a one-tailed test presumes a change, as in ANY change in ANY direction has occurred. The proper way to use a one-tailed test is to first do a two-tailed test for change in any direction. If change has occurred, then one can do a one-tailed test in the direction of the change.
Returning to the earlier example of whether I am running slower, suppose I decide I want to test to see if I am not just performing differently (≠), but am actually slower (<). I can do a one tail test at the 95% confidence level. Here alpha will again be 0.05. In order to put all of the area into one tail I will have to use the spreadsheet function TINV(2*α,df).
H0: μ = 6.15
H1: μ < 6.15
μ=6.15
x = 6.38
sx = 1.00
n = 5
degrees of freedom (df)=4
tc = TINV(2*α,df) = TINV(2*0.05,4) = 2.13
t-statistic =
=
(6.38-6.15)/(1.00/sqrt(5)) = 0.51
Note that the t-statistic calculation is unaffected by this change in the problem.
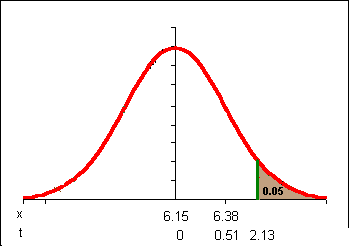
Note that my t-statistic would have to exceed only 2.13 instead of 2.78 in order to achieve statistical significance. Still, 0.51 is not beyond 2.13 so I still DO NOT reject the null hypothesis. I am not really slower, not based on this data.
Thus one tailed tests are identical to two-tailed tests except the formula for tc is TINV(2*α,df) and the formula for p is =TDIST(ABS(t),n−1,1).
Suppose we decide that the 30.53 body fat percentage for females 21+ at the college definitely represents an increase. We could opt to run a one tailed test at an alpha of 0.05.
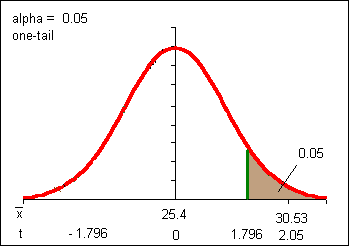
This result should look familiar: it is the result of the two tail test at alpha = 0.10, only now we are claiming we have halved the Type I error rate (α) to 0.05. Some statisticians object to this saying we are attempting to artificially reduce our Type I error rate by pre-deciding the direction of the change. Either that or we are making a post-hoc decision based on the experimental results. Either way we are allowing assumptions into an otherwise mathematical process. Allowing personal decisions into the process, including those involving α, always involve some controversy in the field of statistics.
=TDIST(0.51,4,2) = 0.64
For a sample proportion p and a known or pre-existing population proportion P, a hypothesis can be done to determine if the sample with a sample proportion p could have come from a population with a proportion P. Note that in this text, due to typesetting issues, a lower-case p is used for the sample proportion while an upper case P is used for the population proportion.
In another departure from other texts, this text uses the student's t-distribution for tc providing a more conservative determination of whether a change is significant in smaller samples sizes. Rather than label the test statistic as a z-statistic, to avoid confusing the students and to conform to usage in earlier sections the test statistic is referred to as a t-statistic.
A survey of college students found 18 of 32 had sexual intercourse. An April 2007 study of abstinence education programs in the United States reported that 51% of the youth, primarily students, surveyed had sexual intercourse. Is the proportion of sexually active students in the college different from that reported in the abstinence education program study at a confidence level of 95%?
The null and alternate hypotheses are written using the population proportion, in this case the value reported in the study.
H0: P = 0.51
H1: P ≠ 0.51
sample proportion p = 18/32 = 0.5625
sample proportion q = 1 − p = 0.4375
Note that n*p must be > 5 and n*q must also be > 5 just as was the case in constructing a confidence interval.
Confidence level c = 0.95
The t-critical value is still calculated using alpha α along with the degrees of freedom:
=TINV(0.05,32−1)
=2.04
The only "new" calculation is the t-statistic t:
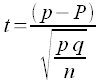
Note that the form is still (sample statistic - population parameter)/standard error for the statistic.
=(0.5625-0.51)/SQRT(0.5625*0.4375/32)
=0.5545
The t-statistic t does not exceed the t-critical value, so the difference is not statistically significant. We fail to reject the null hypothesis of no change.
The p-value is calculated as above using the absolute value of the t-statistic.
=TDIST(ABS(0.5545),32-1,2)
=0.58
The maximum level of confidence c we can have that this difference is significant is only 42%, far too low to say there is a difference.
Many studies investigate systems where there are measurements taken before and after. Usually there is an experimental treatment or process between the two measurements. A typical such system would be a pre-test and a post-test. In-between the pre-test and the post-test would typically be an educational or training event. One could examine each student's score on the pre-test and the post-test. Even if everyone did better on the post-test, one would have to prove that the difference was statistically significant and not just a random event.
These studies are called "paired t-tests" or "inferences from matched pairs". Each element in the sample is considered as a pair of scores. The null hypothesis would be that the average difference for all the pairs is zero: there is no difference. For a confidence interval test, the confidence interval for the mean differences would include zero if there is no statistically significant difference.
When we say the sample mean before is "equal" we mean "statistically equal," not mathematically equal. We mean that there is no statistically significant difference between the before and after means at some level of confidence. Statistically speaking we say that the two samples could come from the same population.
In case II the difference in the sample means is too large for that difference to likely be zero. Statistically speaking we say that the two samples come from different populations.
If the difference for each data pair is referred to as d, then the mean difference could be written d. The hypothesis test is whether this mean difference d could come from a population with a mean difference μd equal to zero (the null hypothesis). If the mean difference d could not come from a population with a mean difference μd equal to zero, then the change is statistically significant. In the diagram above the mean difference μd is equal to μbefore − μ after.
Consider the paired data below. The first column are female body fat measurements from the beginning of a term. The second column are the body fat measurements sixteen weeks later. The third column is the difference d for each pair.
| BodyFat before | Bodyfat after | Bodyfat difference d |
|---|---|---|
| 23.5 | 20.8 | -2.7 |
| 28.9 | 27.5 | -1.4 |
| 29.2 | 28.4 | -0.8 |
| 24.7 | 24.1 | -0.6 |
| 26.4 | 26.1 | -0.3 |
| 23.7 | 24 | 0.3 |
| 46.9 | 47.2 | 0.3 |
| 23.6 | 24 | 0.4 |
| 26.4 | 27.1 | 0.7 |
| 15.9 | 17 | 1.1 |
| 30.3 | 31.5 | 1.2 |
| 28.0 | 29.3 | 1.3 |
| 36.2 | 37.6 | 1.4 |
| 31.3 | 32.8 | 1.5 |
| 31.5 | 33.2 | 1.7 |
| 26.7 | 28.6 | 1.9 |
| 26.5 | 29.0 | 2.5 |
The confidence interval is calculated on the differences d (third column above) using the sample size n, sample mean difference d, and the sample standard deviation of the difference data d. The following table includes calculations using a 95% confidence interval.
| Count of the differences | 17 |
| sample mean difference d | 0.50 |
| Standard deviation of the difference data d | 1.33 |
| Standard error for the mean of the difference data d | 0.32 |
| tc for confidence level = 0.95 | 2.12 |
| Margin of the error E for the mean | 0.68 |
| Lower bound for the 95% confidence interval | -0.18 |
| Upper bound for the 95% confidence interval | 1.18 |
The 95% confidence interval includes a possible population mean of zero. The population mean difference μd could be equal to zero.

This means that "no change" is a possible population mean. To use the double negative, we cannot rule out the possibility of no change. We fail to reject the null hypothesis of no change. The women have not statistically significantly gained body fat over the sixteen weeks of the term.
Spreadsheets provide a function to calculate the p-value for paired data using the student's t-distribution. This function is the TTEST function. If the p-value is less than your chosen risk of a type I error α then the difference is significant. The function does not require generating the difference column d as seen above, only the original data is used in this function.
The function takes as inputs the before data (data_range_pre), the after data (data_range_post), the number of tails, and a final variable that specifies the type of test. A paired t-test is test type number one.
=TTEST(data_range_pre,data_range_post,2,1)
To ensure that the spreadsheet calculates the p-value correctly, delete any data missing the pre or post value in the pair. Data missing a pre or post value is not paired data!
Note too that while many paired t-tests for a difference of sample means involve pre and post data, there are situations in which the paired data is not pre and post in terms of time.
The smallest alpha for which we could say the difference is statistically significant is 1 − p-value. That said, alpha should be chosen prior to running the hypothesis test.
| p-value | 0.14 |
| Maximum confidence level c | 0.86 |
The p-value confirms the confidence interval analysis, we fail to reject the null hypothesis. At a 5% risk of a type I error we would fail to reject the null hypothesis. We can have a maximum confidence of only 86%, not the 95% standard typically employed. Some would argue that our concern for limited the risk of rejecting a true null hypothesis (a type I error) has led to a higher risk of failing to reject a false null hypothesis (a type II error). Some would argue that because of other known factors - the high rates of diabetes, high blood pressure, heart disease, and other non-communicable diseases - one should accept a higher risk of a type I error. The average shows an increase in body fat. Given the short time frame (a single term), some might argue for reacting to this number and intervening to reduce body fat. They would argue that given other information about this population's propensity towards obesity, 86% is "good enough" to show a developing problem. Ultimately these debates cannot be resolved by statisticians.
The TTEST function allows one to calculate the p-value directly from two samples. One does not even have to calculate the means in order to use the TTEST function.
If one has chosen to use an alpha of 5%, then a p-value of less than 0.05 indicates that the means are statistically significantly different, and we would reject the null hypothesis of no difference between the means. The means are not statistically equal.
If the p-value is larger than 0.05, then the means are not statistically significantly different, and we would fail to reject the null hypothesis. The means are statistically equal.
When the p-value is MORE than our chosen risk of a type I error alpha (usually 0.05):
When the p-value is LESS than our chosen risk of a type I error alpha (usually 0.05):
One of the more common situations is when one is seeking to compare two independent samples to determine if the means for each sample are statistically significantly different. In this case the samples may differ in sample size n, sample mean, and sample standard deviation.
In this text the two samples are referred to as the x1 data and the x2 data. The use of the same variable, x, refers to a comparison of sample means being a comparison between two variables that are the same. The test is to see whether the two samples could both come from the same population X. The sample size for the x data is nx1. The sample mean for the x1 data is x1. The sample standard deviation for the x1 data is sx1. For the x2 data, the sample size is nx2, the sample mean is x2, and the sample standard deviation is sx2.
When we say the sample means are "equal" we mean "statistically equal," not mathematically equal. We mean that there is no statistically significant difference between the two sample means. Statistically speaking we say that the two samples could come from the same population.
In case II the difference in the sample means is too large for that difference to likely be zero. Statistically speaking we say that the two samples come from different populations.
Two possibilities exist. Either the two samples come from the same population and the population mean difference is statistically zero. Or the two samples come from different populations where the population mean difference is statistically not zero.
Note the sample mean tests are predicated on the two samples coming from populations X1 and X2 with population standard deviations σ1 = σ2 where the capital letters refer to the population from which the x1 and x2 samples were drawn respectively. "Fortunately it can usually be assumed in practice that since we most often wish to test the hypothesis that µ1 = µ2; it is rather unlikely that the two distributions should have the same means but different variances." (where the variance is the square of the standard deviation). [M. G. Bulmer, Principles of Statistics (Dover Books on Mathematics), Dover Publications (April 26, 2012)]. That said, knowledge of the system being studied and an understanding of population distribution would be important to a formal analysis. In this introductory text the focus is on basic tools and operations, providing a foundation on which to potentially build a more nuanced understanding of statistics.
When working with two independent samples, testing for a difference of means can also be explored using confidence intervals for each sample. Confidence intervals for each sample provide more information than a p-value and the declaration of a significant difference is more conservative. Confidence intervals for each sample cannot sort out the indeterminate case where the intervals overlap each other but not the other sample mean. The following diagrams show three different possible relationships between the confidence intervals and the mean. There are more possibilities, these are meant only as samples for guidance. Sample one has a sample mean x1, sample two has a sample mean x2.
The following is another confidence interval approach to determining whether two samples have different means. Where the approach above charts the confidence intervals separately, this approach looks at whether the confidence interval for the difference in the means could include a population mean difference of zero. Note that this approach would not lead to proving that the population mean difference is zero. That is not being proved, a population mean difference of zero is taken as a given by the null hypothesis. The test is whether that null model can be rejected, whether the null model is false, not whether the null model is true.
Each sample has a range of probable values for their population mean μ. If the confidence interval for the sample mean differences includes zero, then there is no statistically significant difference in the means between the two samples. If the confidence interval does not include zero, then the difference in the means is statistically significant.
Note that the margin of error E for the mean difference is still tc multiplied by the standard error. The standard error formula changes to account for the differences in sample size and standard deviation.
Image variation of the above formula using x and y for the two samples for browsers that do not support MathML:
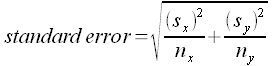
Thus the margin of error E can be calculated using:
Image variation of the above formula using x and y for the two samples for browsers that do not support MathML:
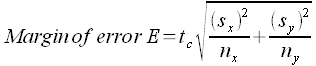
For the degrees of freedom in the t-critical tc calculation use n − 1 for the sample with the smaller size. This produces a conservative estimate of the degrees of freedom. Advanced statistical software uses another more complex formula to determine the degrees of freedom.
The confidence interval is calculated from:
(x1 − x2) − E < (μx1 − μx2) < (x1 − x2) + E
Where x1 is the sample mean of one data set and x2 is the sample mean of the other data. Some texts use the symbol xd for this difference and μd for the hypothesized difference in the population means. This leads to the more familiar looking formulation:
xd − E < μd < xd + E
Where:
μd = μx1 − μx2 and
xd = x1 − x2
Remember, μx1 and μx2 are not known. These are left as symbols. After calculating the interval, check to see if the confidence includes zero. If zero is inside the interval, then the sample means are not significantly different and we fail to reject the null hypothesis.
The following table uses a local business example. Data was recorded as to how many cup of sakau were consumed per customer in a single night at two sakau markets on Pohnpei. The variable is the number of cups of sakau consumed per customer per night. Each column is measuring the same variable. Here on Pohnpei the implication is that the lower the mean (average), the stronger the sakau. Even if there is a difference in the mean, that difference is not necessarily significant. Statistical tests can help determine whether a difference is significant.
| Song mahs (x1) | Rush Hour (x2) |
|---|---|
| 2 | 2 |
| 3 | 10 |
| 6 | 1.5 |
| 3 | 5.5 |
| 3.5 | 9 |
| 4.5 | 7.5 |
| 1 | 5.5 |
| 5 | 3 |
| 3 | 3 |
| 7 | 6 |
| 4 | 3 |
| 2.5 | 4.5 |
| 5.5 | 10 |
| 2 | 9 |
| 1 | 2 |
| 2 | 2 |
| 4 | |
| 5 | |
| 5 | |
| 5.5 | |
| 15 | |
| 14 | |
| 2 | |
| 2 | |
| 4 |
| Sample statistics | ||
|---|---|---|
| sample size n | 16 | 25 |
| sample mean | 3.44 | 5.6 |
| sample stdev | 1.77 | 3.73 |
| Confidence interval statistics | ||
| standard error | 0.87 | |
| t-critical tc | 2.13 | |
| margin of error E | 1.85 | |
| difference of means | -2.16 | |
| lower bound ci | -4.01 | |
| upper bound ci | -0.31 | |
Note that 15 was used for the degrees of freedom in the t-critical calculation. Sixteen is the sample size of the smaller sample.

Note that the confidence interval does not include zero. The confidence interval indicates that whatever the population mean difference μd might be, the population mean μd cannot be zero. This means that the sample means are statistically significantly different. We would reject a null hypothesis of no difference between the two markets. The implication is that Song Mahs is stronger than Rush Hour, at least on these two nights. Bear in mind that while the difference in the sample means is significant for the chosen risk of a type I error alpha, the difference may or may not be important. Whether a difference is a small, medium, or large difference - how "important" the difference might be - cannot be determined from a hypothesis test alone. Effect size will need to be considered, and an understanding of the nature of the system that generated the data is also required. For a sakau drinker paying by the cup on a tight budget, a six cups is twice as expensive as a three cups.
As noted above, spreadsheets provide a function to calculate p-values. If the the p-value is less than your chosen risk of a type I error α then the difference is significant.
The function takes as inputs one the data for one if the two samples (data_range_x1), the data for the other sample (data_range_x2), the number of tails, and a final variable that specifies the type of test. A t-test for means from independent samples is test type number three.
=TTEST(data_range_x1,data_range_x2,number of tails,3)
For the above data, the p-value is given in the following table:
| p-value | 0.02 |
| Maximum confidence level c | 0.98 |
The TTEST function does not use the smaller sample size to determine the degrees of freedom. The TTEST function uses a different formula that calculates a larger number of degrees of freedom, which has the effect of reducing the p-value. Thus the confidence interval result could produce a failure to reject the null hypothesis while the TTEST could produce a rejection of the null hypothesis. This only occurs when the p-value is close to your chosen α.
When the p-value is MORE than our chosen risk of a type I error alpha (usually 0.05):
When the p-value is LESS than our chosen risk of a type I error alpha (usually 0.05):
If you have doubts and want to explore further, take the difference of the means and divide by the standard error to obtain the t-statistic t. Then use the TDIST function to determine the p-value, using the smaller sample size − 1 to calculate the degrees of freedom.
Image variation of the above formula using x and y for the two samples for browsers that do not support MathML:
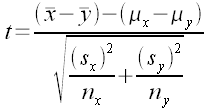
Note that (μ1 − μ2) is presumed to be equal to zero. Thus the formula is the difference of the means divided by the standard error (given further above).
t = xd ÷ (standard error)
Once t is calculated, use the TDIST function to determine the p-value.
=TDIST(ABS(t),n−1,2)
The effect size is whether a difference is small, medium, or large. The effect size can only be calculated if there is a significant difference in the means.
If there is no significant difference in the means then there is no effect size. If the result was a failure to reject the null hypothesis, then the effect size is meaningless and should not be reported.
The p-value provides information on how "surprising" is a result. A significant difference is surprising. The p-value does not tell one whether the difference is meaningful. For large sample sizes small differences might be surprising but not meaningful.
Suppose a pharmaceutical company has a treatment that cures a head cold in seven and a quarter days. Then they develop a new treatment that cures a head cold in seven days. Based on the p-value, the company might find that the difference is significant. The quarter day difference, however, might not be that meaningful.
For two sample means, the effect size provides an estimate of the standardized mean difference between two sample means. The effect size is mathematically related to z-scores. The effect size for a difference of independent sample means is referred to as Cohen's effect size d.
The effect size for two sample means can be calculated from:
where sp is the pooled standard deviation:
Entering the pooled standard deviation in a spreadsheet requires a triple parentheses:
=SQRT(((n1-1)*s1^2+(n2-1)*s2^2)/(n1+n2-2))
...where:
n1 is the sample size for sample one
s1 is the sample standard deviation for sample one
n2 is the sample size for sample two
s2 is the sample standard deviation for sample two
Interpreting whether the difference in sample means has "meaning" in terms of the experiment is complex. Cohen provided some general guidelines. He also cautioned that these interpretations should be used with care. That said, in a beginning statistics course the guidelines provide a way to start thinking about effect size.
Cohen suggested that in the behavioral sciences an effect size of 0.2 is small, an effect size of 0.5 is medium, and an effect size of 0.8 is large. These values may not be correct for other fields of study. Educators in particular have noted that "small" effect sizes may still be important in education studies. The effect size is also affected by whether the data is normally distributed and is free of bias.
| Effect Size | d |
|---|---|
| Very Small | 0.01 |
| Small | 0.20 |
| Medium | 0.50 |
| Large | 0.80 |
| Very Large | 1.20 |
| Huge | 2.0 |
Think of effect size as a way to begin looking at whether the difference has real meaning, not just whether the difference is "surprising" from a p-value perspective. For more information on effect size start with It's the Effect Size, Stupid: What effect size is and why it is important.
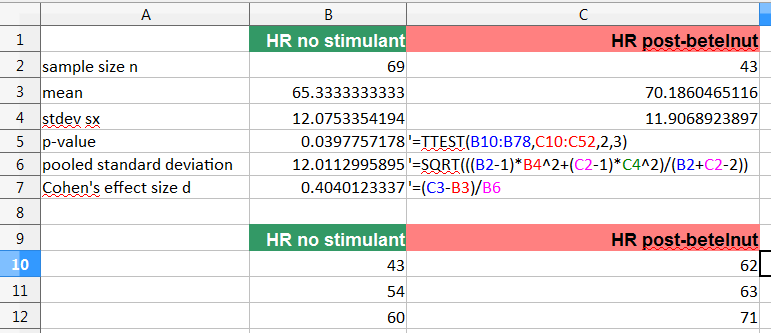
Cohen's effect size d calculation in a spreadsheet.
Instructor provides data of their choice for open data exploration.
Note that above list of questions are those appropriate for a student in an introductory statistics course for use in exploring data in ways that demonstrate knowledge of basic statistical functions. If one is a researcher with some knowledge of statistics, then the questions to be asked will differ. For guidance to a researcher looking to engage in effective statistical practice the following guidelines were suggested by Kass, Caffo, Davidian, Meng, Yu, and Reid in 2016:
For details on how to implement these recommendations, see Ten Simple Rules for Effective Statistical Practice
Another way to tackle analysis of the data is to explore the number and nature of the variables being presented. How many variables? What level of measurement? In introductory statistics one is usually either exploring basic statistics, running correlations, or comparing means.
Data is often organized into tables. In statistics columns are often variables while rows are individual data values. This is not always true, but in introductory statistics this is almost always true. If there is a single data column, then there is one variable. If there are two data columns, then there are two variables. The variable name and the units, if any, are usually listed in the first row of the table.
What can be analyzed, what can be done, depends in part on how many variables are present and the level of measurement. The following chart is for ratio level data. Note that basic statistics can be calculated for any ratio level variable. Remember that columns are variables.
There is a caveat in using this approach, one best captured by the article Ten Simple Rules for Effective Statistical Practice:
While it is obvious that experiments generate data to answer scientific questions, inexperienced users of statistics tend to take for granted the link between data and scientific issues and, as a result, may jump directly to a technique based on data structure rather than scientific goal. For example, if the data were in a table, as for microarray gene expression data, they might look for a method by asking, “Which test should I use?” while a more experienced person would, instead, start with the underlying question, such as, “Where are the differentiated genes?” and, from there, would consider multiple ways the data might provide answers. Perhaps a formal statistical test would be useful, but other approaches might be applied as alternatives, such as heat maps or clustering techniques.
With that in mind, for the student in an introductory statistics course where the objective is to practice statistical operations, an data structures approach is arguably appropriate. The data structures do sometimes provide information on what can be done with the data.
In the chart above there are three data layouts: single variable, two variables with the same sample sizes n, and two variables with different sample sizes n.
Any and all variables can be analyzed by the basic statistics - each column can be analyzed for measures of the middle and spread. The measures of the middle and spread that are appropriate will depend on the level of measurement.
The single variable can be explored for outliers. For a single variable box plots, frequency tables, and histograms may be appropriate. A 95% confidence interval for the mean can be calculated. If there is an expected population mean μ, then a hypothesis test can be run to test whether the sample mean is significantly different from that known population mean μ.
If there are two columns with different sample sizes n, then there is a strong probability in an introductory statistics class that a t-test for a difference of means will be called for. Basic statistics for each variable can also be calculated.
When there are two variables with equal sample sizes, then there are three possibilities. The data could be xy coordinate pairs where one is testing to see if the y variable is correlated with the x variable. In this situation the variables are usually different. A second possibility is that the data represents a "before-and-after" set of measurements. A paired t-test for a difference of means is often called for. The variables will be the same, and the elements in each row will be something that was measured twice. The data is called paired data. The third possibility is that the same variable was measured for different elements, not something that was measured twice. In this situation a likely test is an independent samples t-test for a difference of means.
For both the paired data and independent samples data there is also the possibility that one could be testing for a difference of medians or a difference of variances (standard deviations). There are other tests such as sign test, Wilcoxon Signed Rank test, Wilcoxon Man Whitney test, and the F-test for generating p-values in those situations. At present these tests are beyond the scope of this introductory text.
At the introductory level multiple columns where the variables use the same units may be analyzed by basic statistical analyses of each column unless ANOVA and other multi-sample approaches have been taught. If the variables use different units, then an analysis of relationships and correlations may be appropriate. These are intended as general guidelines to help frame one's thinking about data. These recommendations and suggestions are guidelines, not rules.
In the above chart one has multiple variables with the same units for each column. In an advanced course one might be running an analysis of variance, but in this introductory course only basic metrics are likely to be examined. The data can still "tell a story" that can be supported by the citing of the appropriate statistics. While an analysis of variance is beyond the scope of this introductory course, 95% confidence intervals can be used to provide insight into potential significant differences.
Consider whether rows have a meaning. Are rows measuring something from different samples with the same units in each column? At the introductory course level basic statistics, searches for outliers, might be appropriate. Or are the rows each a single "data point" with each column being in different units? Then there is a greater likelihood that looking for correlations among the columns might a useful approach.
Where there are multiple columns of data and each column contains a different variable, typically from a single sample, then there is the possibility that a correlation analysis will produce useful information on whether the variables are related to each other or not.
Note that the above variables analysis presumes that the first column will be treated as "x" data and the subsequent columns as "y" data. Data does not have to be arranged this way, but in an introduction to statistics this arrangement is rather likely. Depending on the questions asked of the data, running correlations between the first and each subsequent column in a pairwise fashion might provide insight into whether relationships exist between the data columns.
A third way to tackle open data exploration in an introductory statistics course is to consider the statistical tools one has learned to work with during the course. One can be 95% confident that the instructor has chosen a problem that can be resolved by the tools taught in the course. In the "wild" there are many more tools to consider. F-tests for a difference of variances (standard deviations), confidence intervals for a slope, tests for differences of medians, tests for normality. All of these are beyond the scope of this particular text. Thus the student is left with basic statistics (chapters one, two, three), correlations (chapter four), confidence intervals (chapter nine), hypothesis tests against a known mean (chapter ten), and tests for a difference in two sample means (chapter eleven). Those are the tools that have been covered, in the course an open data exploration exercise is likely to utilize those same tools.