MS 150 Statistics FX fall 2005 • Name:

Part I: Basic Statistics

Color can be described in many different ways. There are color words such as red, orange, yellow, green, and blue. In optical physics each color is described by a wavelength and frequency of light.

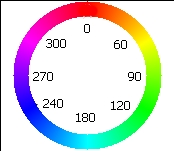
A third way to describe color is by using a color wheel or circle. The word hue is used for the word color when working with a color wheel. On a color wheel the colors are arranged in a circle in the same order that the colors appear in a rainbow. While in art class one learns that the primary colors for paint are red, yellow, and blue; the primary colors for light are different. The primary colors of light are red, green, and blue.

Red, the first color in the rainbow, is placed at the top and is assigned a color angle (or hue angle) of 0°. Once around a circle is 360°. Green is placed one third of the way around the circle at 120°. Blue is placed two-thirds of the way around the circle at 240°.

In the first section the image of a rainbow was analyzed from red to purple, with the hue angles being recorded at equal distances across the face of the rainbow.

The web page uses Cascading Style Sheets 3 Color Module HSL color values and requires the use of a browser that supports CSS3 such as Firefox.

Data sheet

For the hue angle data given in the table:

1. _________ What level of measurement is the hue angle data?
2. _________ Determine the sample size n.
3. _________ Calculate the sample mean x.
4. _________ Determine the median.
5. _________ Determine the mode.
6. _________ Determine the minimum.
7. _________ Determine the maximum.
8. _________ Calculate the range.
9. _________ Calculate the sample standard deviation sx.
10. _________ Calculate the sample Coefficient of Variation.
11. _________ Determine the class width. Use 6 bins (classes or intervals)
12. Fill in the following table with the class upper limits in the first column, the frequencies in the second column, and the relative frequencies in the third column

    Bins	Frequency	Relative Frequency f/n
    _________	_________	_________
    _________	_________	_________
    _________	_________	_________
    _________	_________	_________
    _________	_________	_________
    _________	_________	_________
    Sums:	_________	_________

13. Sketch a histogram of the relative frequency data on the back of the paper.
14. __________________ What is the shape of the distribution?

Part II: Confidence Intervals

Construct a 95% confidence interval for the population mean µ hue angle for a rainbow. Note that n is less than 30. Use the sample size n, sample mean x and sample standard deviation sx from questions two, three, and nine above to generate your t-critical t_c and error tolerance E.

15. __________ What is the point estimate for the population mean µ?
16. df = __________ How many degrees of freedom?
17. t_c = __________ What is t_c?
18. The error tolerance E = _______________
19. The 95% confidence interval for the rainbow hue angle µ is ____________ ≤ µ ≤ ____________
20. Sir Isaac Newton labeled the colors of the rainbow as Red-Orange-Yellow-Green-Blue-Indigo-Violet. Newton put green with a hue angle of 120° at the middle as the mean hue angle. Is a population mean hue angle of 120° a possible mean hue angle for a rainbow based on the above sample?

Part III: Hypothesis Testing

On a color wheel or circle, the mean hue angle is cyan at 180° degrees. Test the hypothesis that the population mean µ hue angle for a rainbow is 180° degrees, in other words, that the middle of the rainbow is actually cyan. Use 180° for the population mean µ. Use the sample size n, sample mean x and sample standard deviation sx from questions two, three, and nine. Use an alpha of α = 0.05 for the hypothesis test.

21. Write the null hypothesis:
22. Write the alternate hypothesis:
23. Write down the level of significance. alpha α = __________
24. Determine t_c. t_c = __________
25. Calculate the t-statistic. t = __________
26. Determine the p-value using the t-distribution. p = __________
27. __________ What is the largest confidence interval c for which this difference is statistically significant?
28. ________________________________________ Would we reject the null hypothesis or fail to reject the null hypothesis that the mean hue angle of 180° degrees is statistically significantly different from the mean in question three at a 5% level of significance?
29. __________ If we reject the null hypothesis, what is the risk of a type I error based on the p-value?

Part IV: Linear Regression

This section explores whether the hue angle changes linearly as one moves from red to magenta across a rainbow. The image of a rainbow was analyzed from red to purple. The hue angle for every 15^th picture element (pixel) was measured and recorded.

30. _________ Calculate the slope of the best fit (least squares) line for the data.
31. _________ Calculate the y-intercept of the best fit (least squares) line.
32. _________ Is the correlation positive, negative, or neutral?
33. _________ Use the equation of the best fit line to calculate the predicted hue angle for pixel 145.
34. _________ Use the inverse of the best fit line to calculate the predicted pixel for a hue angle of 220°.
35. _________ Calculate the linear correlation coefficient r for the data.
36. _________ Is the correlation none, low, moderate, high, or perfect?
37. _________ Calculate the coefficient of determination.
38. _________ What percent of the variation in the pixel data explains the variation in the hue angle data?
39. _________ Is there a relationship between the pixels and the hue angles?
40. _________ Can we use a linear regression to predict hue angles from pixels?
41.      Why or why not?

Tables of Formulas and Excel functions

Basic Statistics
Statistic or Parameter	Symbol	Equations	Excel
Square root			=SQRT(number)
Sample standard deviation	sx or s		=STDEV(data)
Sample Coefficient of Variation	CV	sx/x	=STDEV(data)/AVERAGE(data)

Confidence interval statistics
Statistic or Parameter	Symbol	Equations	Excel
Degrees of freedom	df	= n-1	=COUNT(data)-1
Find a zc value from a confidence level c	zc		=ABS(NORMSINV((1-c)/2))
Find a tc value from a confidence level c	tc		=TINV(1-c,df)
Calculate an error tolerance E of a mean for n < 30 using sx. Should also be used for n ≥ 30.	E		=tc*sx/SQRT(n)
Calculate a confidence interval for a population mean µ from a sample mean x and an error tolerance E		x-E≤ µ ≤x+E
Hypothesis Testing
Calculate t-critical for a two-tailed test	tc		=TINV(α,df)
Calculate a t-statistic	t		=(x - µ)/(sx/SQRT(n))
Calculate a two-tailed p-value from a t-statistic	p		= TDIST(ABS(t),df,2)

Linear Regression Statistics
Statistic or Parameter	Symbol	Equations	Excel
Slope	b		=SLOPE(y data, x data)
Intercept	a		=INTERCEPT(y data, x data)
Correlation	r		=CORREL(y data, x data)
Coefficient of Determination	r2		=(CORREL(y data, x data))^2

Performance charts

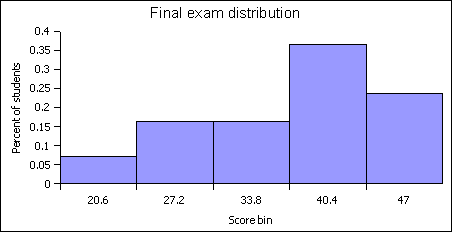
Score distribution on the final examination:

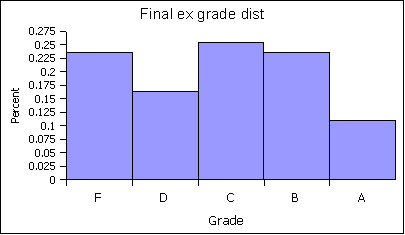
Grade distribution on final examination only:

Grade distribution for the course: