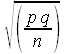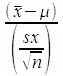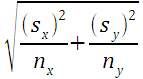Jump Rope • Name:
Data
| Jumps |
|---|
| 102 |
| 79 |
| 68 |
| 66 |
| 61 |
| 69 |
| 42 |
| 45 |
| 79 |
| 22 |
| 43 |
| 13 |
| 24 |
| 10 |
| 11 |
| 107 |
| 17 |
| 34 |
| 8 |
| 20 |
| 58 |
| 26 |
| 45 |
| 40 |
| 111 |
| 105 |
| 213 |
Part I: Basic Statistics
On Thursday 08 November 2007 a jump rope contest was held at a local elementary school festival. Data for this final derives from this contest. Contestants jumped with their feet together, a double-foot jump. The data seen in the table is the number of jumps for twenty-seven female jumpers. A data sheet contains this same data and should be used to avoid typing errors. Note that while the number of jumps data is discrete, treat the data as if it were continuous data.
- _________ Determine the sample size n.
- _________ Determine the minimum.
- _________ Determine the maximum.
- _________ Calculate the range.
- _________ Calculate the midrange.
- _________ Determine the mode.
- _________ Determine the median.
- _________ Calculate the sample mean x.
- _________ Calculate the sample standard deviation sx.
- _________ Calculate the sample Coefficient of Variation.
- _________ Determine the bin width. Use five bins (classes or intervals).
- Fill in the following table with the class upper limits in the first column, the frequencies in the second column, and the relative frequencies in the third column
| Bins (x) | Frequency f | RF p(x) |
|---|
| | |
| | |
| | |
| | |
| | |
| Sums: | | |
- Sketch a histogram of the relative frequency data.
- __________________ What is the shape of the distribution?
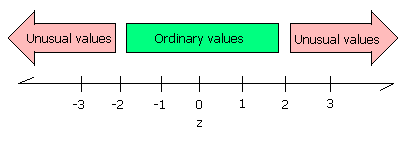
- __________________ Use the sample mean x and sample standard deviation sx above to calculate the z-score for first grader Shana who jumped 11 times.
- _________ Is the z-score for Shana an ordinary or extraordinary value?
- __________________ Use the sample mean x and sample standard deviation sx above to calculate the z-score for fourth grader Demi who jumped 213 times.
- _________ Is the z-score for Demi an ordinary or extraordinary value?
- _________ After Demi's 213 jump performance, the other jumpers retired from the field and no one tried to better her number of jumps. Based on the z-score for Demi, were the other jumpers making a reasonable decision?
- _________ Calculate the standard error of the sample mean x for the number of jumps.
- _________ Find tcritical for a confidence level c of 95% for the number of jumps.
- _________ Determine the margin of error E for the sample mean x.
- Write out the 95% confidence interval for the population mean μ number of jumps:
p(_____________ < μ < ___________) = 0.95
- _________ The population mean number of jumps μ for the boys was 33. Is this a possible population mean for the girls?
- _________ Are the girls statistically significantly better jumpers than the boys?
Part II: Hypothesis Testing using the t-test
While watching the jumping contest I noticed that the girls who were scoring the highest number of jumps appeared to jump at a faster rate than those who scored lower. The jumpers who were jumping a hundred plus times were whipping the rope around at almost two times a second. The girls who jumped less than forty times jumped at a much more leisurely once per second. This did not make intuitive sense. Going slower should have saved energy and allowed one to continue longer. The rate, however, was not consistent, and anecdotal impressions can be deceiving. The very fastest jumper, at 2.27 jumps per second, jumped a below average 45 jumps. Only statistics can tell us if the difference in the mean rates is real or imaginary.
The number of jumps was divided by the time to obtain the number of jumps per second. The number of jumps per second is called the jumping rate. The jumping rates were divided between the rate for those who jumped less than the mean number of jumps and the rate for those who jumped more than the mean number of jumps. If these two samples have statistically significantly different means, then there is a systematic difference in jump rate for jumpers with high jump counts.
[The table is on the next page.]
Jumping rate table
| Jump rate for below average jump count | Jump rate for above average jump count |
|---|
| 1.39 | 1.86 |
| 0.32 | 2.00 |
| 1.01 | 1.63 |
| 0.75 | 1.87 |
| 1.21 | 1.35 |
| 0.95 | 2.10 |
| 0.74 | 1.65 |
| 1.19 | 1.68 |
| 1.17 | 1.82 |
| 1.09 | 1.40 |
| 1.92 | 1.64 |
| 1.68 | 1.51 |
| 0.93 | |
| 1.82 | |
| 2.27 | |
- _________ Calculate the sample mean x for the jump rate for low count data.
- _________ Calculate the sample mean y for the jump rate for high count data.
- _________ Are the sample means for the two samples mathematically different?
- _________ Calculate the degrees of freedom using the smaller of the two sample sizes.
- _________ Calculate the tcritical using alpha α = 0.05 and the degrees of freedom.
- _________ Calculate the standard error SE for two independent samples.
- _________ Calculate the margin of error E for two independent samples.
- ____________ < μd < _____________ Determine the 95% confidence interval for the population mean difference μd
- _________ Does the confidence interval include a mean difference of zero?
- __________________ What is the p-value? Use the difference of means for independent samples TTEST function =TTEST(data_range_x;data_range_y;2;3) to determine the p-value for this two sample data.
- __________________ Is the difference in the mean jump rate statistically significant at a risk of a type I error alpha α = 0.05?
- __________________ Would we "fail to reject" or "reject" a null hypothesis of no difference in the mean jump rate between the girls with a low jump count and a high jump count?
- __________________ What is the maximum level of confidence we can have that the difference is statistically significant?
Part III: Linear Regression (best fit or least squares line)
Jump rate versus count
| Rate | Count |
|---|
| 1.68 | 102 |
| 1.65 | 79 |
| 1.87 | 68 |
| 1.63 | 66 |
| 2.00 | 61 |
| 1.35 | 69 |
| 1.68 | 42 |
| 2.27 | 45 |
| 2.10 | 79 |
| 0.74 | 22 |
| 0.93 | 43 |
| 0.75 | 13 |
| 1.19 | 24 |
| 0.32 | 10 |
| 1.01 | 11 |
| 1.40 | 107 |
| 1.21 | 17 |
| 1.09 | 34 |
| 1.39 | 8 |
| 0.95 | 20 |
| 1.86 | 58 |
| 1.17 | 26 |
| 1.82 | 45 |
| 1.92 | 40 |
| 1.64 | 111 |
| 1.82 | 105 |
The data in this section continues the exploration of jump rate versus the jump count. The jump rate in jumps per second is the independent variable x. The total number of jumps (jump count) is being treated as the dependent variable y. Do not try to type this data in, use the data sheet instead.
- _________ Calculate the slope of the linear regression (best fit line).
- _________ Calculate the y-intercept of the linear regression (best fit line).
- _________ Is the relation between jump rate and jump count positive, negative, or neutral?
- _________ Calculate the linear correlation coefficient r for the data.
- ______________ Is the correlation none, weak/low, moderate, strong/high, or perfect?
- ______________ Determine the coefficient of determination.
- ______________ What percent in the variation in jump rate "explains" the variation in the jump count?
- _________ Use the slope and intercept to predict the number of jumps for a jumper with a jump rate of 1.00
- _________ Use the slope and intercept to determine the rate necessary to obtain 213 jumps.
Tables of Formulas and OpenOffice Calc functions
| Hypothesis testing for paired data samples |
|---|
| Statistic or Parameter | Symbol | Equations | OpenOffice |
|---|
| Calculate a p-value for the difference of the means from two samples of paired data |
=TTEST(data_range_x;data_range_y;2;1) |