MS 150 Statistics fx fall 2006 • Name:

Song mahs
Cups
3
3
3.5
3.5
2
3
4
1
8
3
9
3
7
6
7
10
5
4
2
2
1
1.5
7
2
3.5
1.5
1
8
3
3

Part I: Basic Statistics

The final examination this term takes its data from a local business example. Although the business is unique, the analysis would apply to any small business operating in a highly competitive environment. The data on the right records the number of cups purchased per person at Song Mahs sakau en Pohnpei market for 30 customers on one evening. The data is also available in a data sheet to save you retyping the data.

Data sheet

For the number of cups data given in the table:

  1. _________ What level of measurement is the data?
  2. _________ Determine the sample size n.
  3. _________ Calculate the sample mean x.
  4. _________ Determine the median.
  5. _________ Determine the mode.
  6. _________ Determine the minimum.
  7. _________ Determine the maximum.
  8. _________ Calculate the range.
  9. _________ Calculate the sample standard deviation sx.
  10. _________ Calculate the sample Coefficient of Variation.
  11. _________ Determine the class width. Use six bins (classes or intervals). Note that the number of bins is six!
  12. Fill in the following table with the class upper limits in the first column, the frequencies in the second column, and the relative frequencies in the third column
    BinsFrequencyRF p(x)
    ___________________________
    ___________________________
    ___________________________
    ___________________________
    ___________________________
    ___________________________
    Sums:__________________
  13. Sketch a histogram of the relative frequency data.
  14. __________________ What is the shape of the distribution?

Part II: Estimated mean from a distribution

Data on the number of cups purchased per person for 193 customers was gathered from Nan kahp, Pwopwihda, Rush Hour, and Song Mahs markets.

Four market survey data
Bins x (cups)Freq f RF or P(x)x*P(x)
1390.2020.20
2460.2380.48
3470.2440.73
4310.1610.64
5140.0730.36
6160.0830.50
Sums:1931.0002.91
  1. __________________ What is the estimated population mean number of cups for these 193 customers?
  2. __________________ What is the mode for the number of cups?
  3. __________________ Based on the above table, what is the probability that a customer will buy only one cup of sakau at these markets?
  4. __________________ Toughie: What is the median for the number of cups?

Part III: Confidence Interval

A sample size n of twenty-seven customers at Nan kahp market purchased a sample mean x 3.19 cups with a sample standard deviation sx of 2.06 cups. Construct a 95% confidence interval for the population mean µ number of cups for Nan kahp based on the data provided. Note that n is less than 30.

  1. ____________ What would be the point estimate for the population mean µ number of cups?
  2. df = __________ Find the number of degrees of freedom.
  3. tc = __________ Find tcritical.
  4. E = _______________ Find the margin of error for the mean E.
  5. Calculate the 95% confidence interval for the population mean µ:
    ____________ ≤ µ ≤ ____________
  6. __________ The population mean µ number of cups purchased per customer is 3.93 at Song Mahs. Is a population mean of 3.93 a possible population mean for Nan kahp market based on the 95% confidence interval?
  7. __________ Is the Nan kahp sample mean x of 3.19 statistically significantly different from the Song mahs population mean µ number of cups purchased per customer of 3.93?

Part IV: Hypothesis Testing

A sample size n = 27 customers at Nan kahp sakau market purchased a sample mean x = 3.19 cups with a sample standard deviation sx = 2.06 cups. A study across multiple nights and a number of different markets on Pohnpei established a population mean µ = 3.65 cups purchased per customer. If the Nan kahp data is statistically significantly different than the population mean, then Nan kahp sakau could be theorized to be stronger than average (3.19 is fewer than 3.65, fewer implies stronger). Run a two-tailed hypothesis test with an alpha of α = 0.05 to test whether the Nan kahp sample mean is statistically significantly different from the known population mean of 3.65 cups.

  1. ________________________________________ Write the null hypothesis in formal statistical format.
  2. ________________________________________ Write the alternate hypothesis in formal statistical format.
    α = 0.05.
  3. tc = __________ Determine tcritical.
  4. t = __________ Calculate the t-statistic.
  5. p = __________ Determine the p-value using the t-distribution.
  6. __________ What is the largest confidence interval c for which this difference is statistically significant?
  7. ________________________________________ Would we reject the null hypothesis or fail to reject the null hypothesis that the sample mean is statistically significantly different from the population mean at a 5% level of significance?
  8. __________ If we reject the null hypothesis, what is the risk of a type I error based on the p-value?
  9. __________ Is the Nan kahp sample statistically significantly different from the population mean?

Nan kahp

Part V: Linear Regression

Distance versus cup mean
Marketdistance
/kilometers		mean cups
per customer
Rush Hour3.05.18
Song Mahs13.53.93
Nan kahp14.03.19
Pwopwida15.52.62

The data in this section examines whether there is a trend in the mean number of cups of sakau purchased per customer with increasing distance in kilometers from Spanish Wall in Kolonia. Zero kilometers is at Spanish Wall.

  1. _________ Calculate the slope of the best fit (least squares) line for the distance versus cups of sakau per customer data.
  2. _________ Calculate the y-intercept of the best fit (least squares) line.
  3. _________ Is the correlation positive, negative, or neutral?
  4. _________ Use the equation of the best fit line to calculate the predicted mean number of cups purchased per customer for a market 10 kilometers from Spanish Wall in Kolonia.
  5. _________ Use the inverse of the best fit line to calculate the predicted distance at which 5 cups is the mean number of cups purchased per customer.
  6. _________ Calculate the linear correlation coefficient r for the data.
  7. _________ Is the correlation none, low, moderate, high, or perfect?
  8. _________ Calculate the coefficient of determination.
  9. _________ What percent of the variation in the distance explains the variation in the mean number of cups purchased?
  10. _________ What is the predicted number of cups which would be purchased at "No choice" market located at Spanish Wall, Kolonia, a distance of zero kilometers?
  11. _________ What is the distance at which the mean number of cups would be predicted to be zero?

The data on this final is based on actual data from real markets here on Pohnpei. The author is deeply indebted to the markets for sharing their proprietary information.

The average number of cups per customer refers to individual named customers. The original data is contained in a separate spreadsheet, minus the customer names.

The average number of cups consumed is not necessarily an indication of the strength of the sakau. Some markets cater to commuters who tend to drink a cup or two on their way home and then head on home. Other markets are destination markets at which customers linger late into the evening engaged in the fine art of conversation.

Tables of Formulas and OpenOffice Calc functions

Basic Statistics
Statistic or ParameterSymbolEquationsOpenOffice
Square root=SQRT(number)
Sample standard deviationsx or s=STDEV(data)
Sample Coefficient of VariationCV sx/x =STDEV(data)/AVERAGE(data)
Confidence interval statistics
Statistic or ParameterSymbolEquationsOpenOffice
Degrees of freedomdf= n-1=COUNT(data)-1
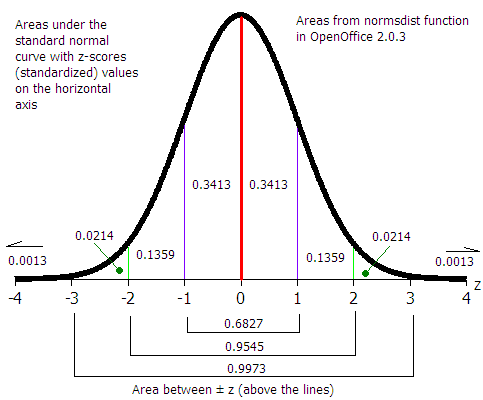
Find a zc value from a confidence level c zc =ABS(NORMSINV((1-c)/2))
Find a tc value from a confidence level c tc =TINV(1-c;df)
Calculate a margin of error for the mean E for n < 30 using sx. Should also be used for n ≥ 30. E error_tolerance_tc.gif (989 bytes) =tc*sx/SQRT(n)
Calculate a confidence interval for a population mean µ from a sample mean x and an error tolerance E   x - E ≤ µ ≤ x + E
Hypothesis Testing
Calculate t-critical for a two-tailed test tc =TINV(α;df)
Calculate a t-statistic t xbartot.gif (1028 bytes) =(x - µ)/(sx/SQRT(n))
Calculate a two-tailed p-value from a t-statisticp = TDIST(ABS(t);df;2)
Linear Regression Statistics
Statistic or ParameterSymbolEquationsOpenOffice
Slopeb=SLOPE(y data; x data)
Intercepta=INTERCEPT(y data; x data)
Correlationr=CORREL(y data; x data)
Coefficient of Determinationr2  =(CORREL(y data; x data))^2

Standard normal distribution Excel: Left to z