The following document is based on the deployed outline. By using the outline as the basis for reporting assessment of learning, the document seeks to close the design-deploy-assess loop in a single document.
Course Description: A one semester course designed as an introduction to the basic ideas of data presentation, descriptive statistics, linear regression, and inferential statistics including confidence intervals and hypothesis testing. Basic concepts are studied using applications from education, business, social science, and the natural sciences. The course uses spreadsheet software for both data analysis and presentation.
| Deployed design | Assessed result1 | |||||||
|---|---|---|---|---|---|---|---|---|
| CLO | PLO 3.1 | PLO 3.2 | PLO 3.3 | ↓ ↑ | CLO | PLO 3.1 | PLO 3.2 | PLO 3.3 |
| 1 | I,D,M | I,D | I,D2 | 1 | 0.90 | 0.66 | 0.56 | |
| 2 | I,D | I | 2 | 0.70 | 0.14 | |||
| 3 | I,D | I,D,M | 3 | 0.76 | ||||
| Deployed design | |||
|---|---|---|---|
| CLO | PLO 3.1 | PLO 3.2 | PLO 3.3 |
| 1 | 1.1 1.3 1.4 1.5 | 1.2 | 1.A3 |
| 2 | 2.1 2.2 2.3 2.4 2.5 | 2.1 | |
| 3 | 3.1 3.2 3.3 | 3.1 3.2 3.3 | |
| Assessed result | ||||
|---|---|---|---|---|
| CLO | SLO | PLO 3.1 | PLO 3.2 | PLO 3.3 |
| CLO1 | 1.1 | 0.56 | 0.31 | |
| 1.2 | 0.75 | 0.73 | 0.56 | |
| 1.3 | 0.95 | |||
| 1.4 | 0.52 | |||
| 1.5 | 0.79 | 0.79 | ||
| CLO2 | 2.1 | 0.19 | 0.14 | |
| 2.2 | 0.78 | |||
| 2.3 | 0.65 | |||
| 2.4 | 0.83 | |||
| 2.5 | 0.71 | |||
| CLO3 | 3.1 | 0.88 | ||
| 3.2 | 0.86 | |||
| 3.3 | 0.58 | |||
| Student learning outcomes | Assessment strategies | iA4 |
|---|---|---|
| 1.1 Identify levels of measurement and appropriate statistical measures for a given level | Quizzes, tests. 60% Passing as per 2009-2011 catalog. Statistics project report. | 0.44 |
| 1.2 Determine frequencies, relative frequencies, creating histograms and identifying their shape visually. | 0.70 | |
| 1.3 Calculate basic statistical measures of the middle, spread, and relative standing. | 0.95 | |
| 1.4 Calculate simple probabilities for equally likely outcomes. | 0.52 | |
| 1.5 Determine the mean of a distribution. | 0.79 |
| Student learning outcomes | Assessment strategies | iA |
|---|---|---|
| 2.1 Calculate probabilities using the normal distribution | Quizzes, tests. 60% Passing as per 2009-2011 catalog | 0.19 |
| 2.2 Calculate the standard error of the mean | 0.78 | |
| 2.3 Find confidence intervals for the mean | 0.65 | |
| 2.4 Perform hypothesis tests against a known population mean using both confidence intervals and formal hypothesis testing | 0.83 | |
| 2.5 Perform t-tests for paired and independent samples using both confidence intervals and p-values | 0.71 |
| Student learning outcomes | Assessment strategies | iA |
|---|---|---|
| 3.1 Calculate the linear slope and intercept for a set of data | Quizzes, tests. 60% Passing as per 2009-2011 catalog | 0.88 |
| 3.2 Calculate the correlation coefficient r | 0.86 | |
| 3.3 Generate predicted values based on the regression | 0.58 |
Beyond detailed information of benefit primarily to the instructor, the failure to assess CLOs 3.1, 3.2, and 3.3 against PLO 3.2 is a gap in the current curriculum. This gap was not evident prior to this analysis. Only this sort of specific aggregating analysis against the deployed outline is likely to have revealed this issue.
Finding a meaningful way to aggregate the data was not obvious. A learning outcome in statistics may include a number of specific, individual skills that must be performed in sequence. The result should be a final correct answer. Thus there is a strong argument to be made that the single outcome which has the fewest number of successful students ought to be used to characterize the overall success rate for the student learning outcome.
The complication is that the minimum, as a function, is statistically problematic. Ultimately one has to aggregate data, and aggregating always to the minimum eventually leads to a zero student success rate. There will always be someone who missed something. For example, no question on the final examination was answered correctly by all of the students. Someone missed each of the 53 questions. On aggregate, the minimum success is assuredly zero.
Hence this report chose to aggregate the average student success rate on questions on the final examination.
MS 150 Statistics has been taught by the same instructor since fall 2000. By 2004 the course content had stabilized and the final examinations were starting to cover the same set of material. In Fall 2005 item analysis data began to be recorded for some final examinations as a way of measuring learning. The table below cites the percent of students who answered questions correctly for the given student learning outcome based on an item analysis of the final examination. Fa refers to fall terms, Sp to spring terms. the number is the year.
| SLO | Fa 05 | Fa 06 | Fa 07 | Sp 08 | Fa 08 | Sp 09 | Fa 09 | Sp 10 | Fa 10 |
|---|---|---|---|---|---|---|---|---|---|
| 1.1 | 0.6 | 0.92 | 0.82 | 0.78 | 0.82 | 0.94 | 0.96 | 0.74 | 0.44 |
| 1.2 | 0.61 | 0.56 | 0.6 | 0.83 | 0.84 | 0.75 | 0.79 | 0.55 | 0.7 |
| 1.3 | 0.89 | 0.91 | 0.87 | 0.9 | 0.8 | 0.86 | 0.93 | 0.74 | 0.95 |
| 1.4 | 0.5 | 0.67 | 0.82 | 0.59 | 0.73 | 0.52 | |||
| 1.5 | 0.77 | 0.52 | 0.75 | 0.79 | |||||
| 2.1 | 0.61 | 0.71 | 0.61 | 0.45 | 0.71 | 0.19 | |||
| 2.2 | 0.74 | 0.84 | 0.84 | 0.87 | 0.91 | 0.64 | 0.78 | ||
| 2.3 | 0.65 | 0.79 | 0.4 | 0.66 | 0.85 | 0.67 | 0.73 | 0.55 | 0.65 |
| 2.4 | 0.7 | 0.69 | 0.64 | 0.36 | 0.56 | 0.55 | 0.55 | 0.46 | 0.83 |
| 2.5 | 0.68 | 0.55 | 0.63 | 0.43 | 0.56 | 0.46 | 0.71 | ||
| 3 | 0.74 | 0.61 | 0.73 | 0.8 | 0.79 | 0.63 | 0.69 | 0.7 | 0.76 |
| 3.1 | 0.95 | 1.61 | 0.9 | 0.91 | 0.95 | 0.85 | 1.00 | 0.79 | 0.88 |
| 3.2 | 0.91 | 0.37 | 0.93 | 0.84 | 0.85 | 0.87 | 0.92 | 0.79 | 0.86 |
| 3.3 | 0.49 | 0.69 | 0.56 | 0.66 | 0.44 | 0.38 | 0.47 | 0.55 | 0.58 |
Performance varies term-to-term. This variation is natural in any sufficiently complex system. Term-on-term rises and falls are not necessarily anything more than random variation. An analysis of the trend over the terms above indicated no statistically significant trend, neither positive nor negative, in any of the student learning outcomes over time, with the possible exception of 2.15.
The lack of a long term trends is not unusual in a "mature course." Success rates were lower in 2000, 2001, and 2002, but not item analysis data is available from that time period. By 2005 the instructor had made many curricular and teaching style adjustments to lift performance in the course. While data from fall 2000 was not available, grade data from spring 2001 provides anecdotal support.
| Grade | Spring 2001 | Fall 2010 |
|---|---|---|
| A | 0.08 | 0.16 |
| B | 0.29 | 0.28 |
| C | 0.29 | 0.33 |
| D | 0.13 | 0.09 |
| F | 0.21 | 0.01 |
Possibly more significant is that a single section with 24 students completed the spring 2001 course. Fall 2010 three sections with a total of 76 students completed the course. The course has effectively tripled in size while improving student learning over the past ten years.
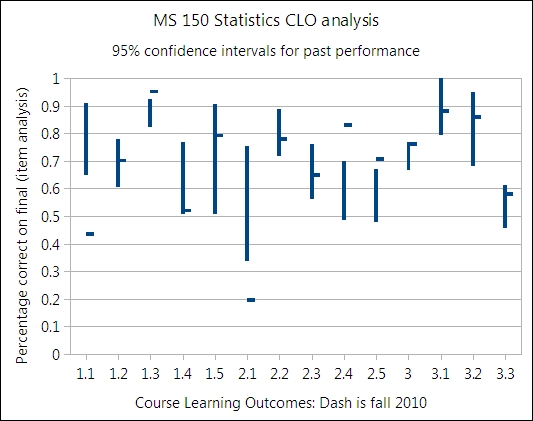
With performance fairly stable over time, one way to sort out real differences from natural variation is to construct a range in which the natural variation typically occurs. One way this range of normally expected performance values can be captured is by constructing the 95% confidence interval for the mean performance. There are issues with doing this as the data is spread over time and involved different final examinations. The confidence intervals, however, remain a good indicator as to whether the increases or decreases in performance seen this year are within the expected range of variation.

The x-axis notes the student learning outcomes (SLOs), where the first digit is the course learning outcome.6 The vertical lines are the ranges in which a given SLO is expected to vary over time. The short horizontal lines are the 2010 value for a given SLO. Where the horizontal line is attached to the vertical line, the performance is well within the natural variation of the performance for that SLO over time.
Where the horizontal line is above or below a vertical line, then there may have been a significant change in the performance on that SLO.
SLO 1.1 saw a significant drop in performance. However, SLO 1.1 was measured in an entirely different and unprecedented manner fall 2010. Prior term values were based on a single question on the final examination with only three possible answers. Fall 2010 a separate assignment was made to challenge the students into critically thinking about levels of measurement. This assignment was exceptionally difficult. The 44% refers to those who correctly assessed the level of measurement, reported only the appropriate statistics, and constructed a correct histogram based on the level of measurement. The instructor had long believed that the performance on this item was artificially inflated by the simplicity of the single question, and the fall 2010 assignment confirmed this belief.
The drop in the performance on 2.1 is also related to a change in measurement.5
Gains were seen in 1.3, 2.4, and 2.5. There were changes in the structure of the final examination from prior terms that increased the number of times students had to calculate the sample mean. There was also the addition of the calculation of the sample sum in the fall 2010 final. The students typically score well on calculating means, thus this alone may have boosted the performance on 1.3.
Causes for the performance improvements seen in 2.4 and 2.5 are not known. There was no specific intervention designed to target those learning outcomes. That material remains some of the most difficult in the course.
MS 150 Statistics had three sections that ran Monday, Wednesday, and Friday for an hour each at 8:00, 9:00, and 10:00. Early in the term there appeared to be the possibility of performance differences due to gender and section time. These differences, however, did not continue during the term and by the end of the term there were no statistically significant differences in these subgroups. The following table details average overall course performance by section and gender, none of the differences was found to be statistically significant.
| Section | Female | Male | Section average |
|---|---|---|---|
| 8:00 | 0.77 | 0.72 | 0.75 |
| 9:00 | 0.85 | 0.73 | 0.79 |
| 10:00 | 0.74 | 0.82 | 0.78 |
| Gender average | 0.79 | 0.75 | Overall avg: 0.77 |
A study spring 2010 did not provide support for a theory that there is a selection effect which puts academically weaker students in the 8:00 section. Fall 2010 also to fails to provide statistically significant evidence that the 8:00 course average is lower than the 9:00 and 10:00 sections. While sample size remains an issue in finding a significant difference, in the strongest possible test using the raw scores of the 8:00 against the 9:00 and 10:00 classes, there was absolutely no significant difference (p-value = 0.51). The instructor's sense that the 8:00 class under performs the other sections is not borne out.
Gender differences were also due to random variation and did not reach a statistically significant difference.
1Average percent of students demonstrating the learning outcome. Average may be based on multiple encounters with the outcome on the final examination.
2Accomplished in part via the statistics project report
3Accomplished via the statistics project report which is part of course level Assessment
4 iA is Assessed result and is based on item analysis of final examination, statistics project, histogram assignment, and analysis of quizzes five, six, and seven for material not present on the final examination. For quizzes five and six, 70% success rates were used as criterion for demonstrating an outcome. The final examination data was strictly based on item analysis - the percent of students who successfully answered questions for that outcome. The other instruments were analyzed for students ability to demonstrate the learning outcome.
5 Fall 2010 2.1 was measured by determining the number of students who scored above 70% on a quiz covering that material during the term. This material was not on the final examination fall 2010. Thus the result is not an item analysis value, as are some of the earlier values. A comparison across time cannot be made.
6 For historical reasons, CLO 3 is also reported. Reports since 2008 combined the student learning outcomes that in 2010 became 3.1, 3.2, and 3.3. Data for 3.1, 3.2, and 3.3 was reconstructed from available files.