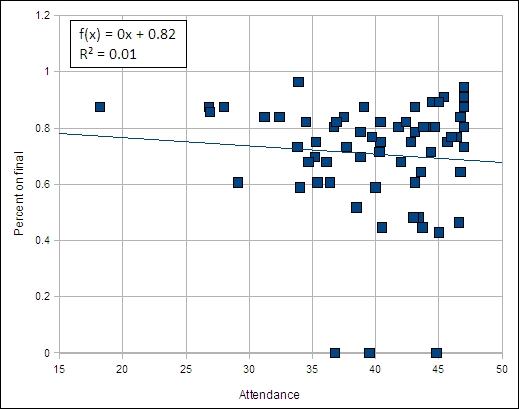
Linear regression trend line attendance (not absences) versus performance in course
Review of performance: MS 150 spring 2010. 64 students were enrolled in course. Submitted by Dana Lee Ling.
| n | SLO | Program SLO | I, D, M | Reflection/comment | |
|---|---|---|---|---|---|
| 1 | Identify levels of measurement and appropriate statistical measures for a given level | define mathematical concepts, calculate quantities, estimate solutions, solve problems, represent and interpret mathematical information graphically, and communicate mathematical thoughts and ideas. | M | 47 | of 64 students were successful on this SLO based on an item analysis of the comprehensive final examination |
| 2 | Determine frequencies, relative frequencies, creating histograms and identifying their shape visually | M | 34 | ||
| 3 | Calculate basic statistical measures of the middle, spread, and relative standing | M | 47 | ||
| 4 | Perform linear regressions finding the slope, intercept, and correlation; generate predicted values based on the regression | M | 44 | ||
| 5 | Calculate simple probabilities for equally likely outcomes | M | 46 | ||
| 6 | Determine the mean of a distribution | M | 48 | ||
| 7 | Calculate probabilities using the normal distribution | M | 45 | ||
| 8 | Calculate the standard error of the mean | M | 40 | ||
| 9 | Find confidence intervals for the mean | M | 35 | ||
| 10 | Perform hypothesis tests against a known population mean using both confidence intervals and formal hypothesis testing | M | 29 | ||
| 11 | Perform t-tests for paired and independent samples using both confidence intervals and p-values | M | 29 | ||
In the table above, n is the outline outcome number. As noted below, outline outcome items five, six, and seven were not directly tested on the final examination. The data for those outcomes above is based on in-class testing data.
Performance in MS 150 Statistics was measured by quizzes and tests throughout the term. A comprehensive final examination consisting of forty-nine fill-in-the-blank questions was administered. Forty-four questions mapped back to a course level student learning outcome. Performance against the outline proposed in 2008 has been measured for the past four terms and provided a basis for comparison across the terms. The following table indicates the percentage of students who correctly answered questions for each outcome on the outline over five terms. The data below derives from an item analysis of the final examination, except for outcomes five, six, and seven. These three outcomes are foundation material for outcomes eight, nine, ten, and eleven. These three outcomes are tested during the term. In the table below quiz data from the term is used to report on success in outcomes five, six, and seven.
| n | Students will be able to... | Sp 08 | Fa 08 | Sp 09 | Fa 09 | Sp 10 |
|---|---|---|---|---|---|---|
| 1 | Identify levels of measurement and appropriate statistical measures for a given level | 0.78 | 0.82 | 0.94 | 0.96 | 0.74 |
| 2 | Determine frequencies, relative frequencies, creating histograms and identifying their shape visually | 0.83 | 0.84 | 0.75 | 0.79 | 0.55 |
| 3 | Calculate basic statistical measures of the middle, spread, and relative standing | 0.9 | 0.8 | 0.86 | 0.93 | 0.74 |
| 4 | Perform linear regressions finding the slope, intercept, and correlation; generate predicted values based on the regression | 0.8 | 0.79 | 0.63 | 0.69 | 0.7 |
| 5 | Calculate simple probabilities for equally likely outcomes | 0.67 | NA | 0.82 | 0.59 | 0.73 |
| 6 | Determine the mean of a distribution | NA | NA | 0.77 | 0.52 | 0.75 |
| 7 | Calculate probabilities using the normal distribution | 0.71 | NA | 0.61 | 0.45 | 0.71 |
| 8 | Calculate the standard error of the mean | 0.84 | 0.84 | 0.87 | 0.91 | 0.64 |
| 9 | Find confidence intervals for the mean | 0.66 | 0.85 | 0.67 | 0.73 | 0.55 |
| 10 | Perform hypothesis tests against a known population mean using both confidence intervals and formal hypothesis testing | 0.36 | 0.56 | 0.55 | 0.55 | 0.46 |
| 11 | Perform t-tests for paired and independent samples using both confidence intervals and p-values | 0.55 | 0.63 | 0.43 | 0.56 | 0.46 |
| 12 | Go beyond outline | NA | 0.33 | 0.16 | 0.37 | 0.44 |
| PSLO | define mathematical concepts, calculate quantities, estimate solutions, solve problems, represent and interpret mathematical information graphically, and communicate mathematical thoughts and ideas. | 0.72 | 0.76 | 0.69 | 0.71 | 0.62 |
Sp refers to spring terms, Fa to fall terms. The digits that follow are the last two digits of the calendar year. Performance marked NA indicates that the material was not directly performed on the final examination and alternative assessment data was not recorded in that term. Quiz based averages from chapters 5, 6, and 7 were not included in the overall average for any term due to performance differences for in-class quizzes.
The 95% confidence interval for the overall mean is 64% to 76%. This term saw a statistically significant drop in performance against this confidence interval for the mean. This collapse in learning is atypical for a mature course. Excluding the quiz based performance data for outline items 5, 6, and 7, performance fell for every single outine item.
The final five questions on the final examination are from material beyond the outline. The students are unaware that this material will appear, the material is not covered in the textbook, and the material is deleted from the posted finals that students use to study for the examination. This material is a complete surprise to the students. The point of this material is noted on the final examination itself, "One intention of any course is that a student should be able to learn and employ new concepts in the field even after the course is over."
The 44% success rate of students on this material is an increase from last term, which was double the performance of the previous term. This value appears to be highly variable from term-to-term.
Questions that required an inference, an interpretation of a result, had only a 45% success rate this term, down from a success rate of 55% the previous term. That 55% success rate was an increase from a 40% success rate the prior term. The current term-on-term drop is reflective of the overall drop in performance seen spring 2010.
For a fourth term in a row students were asked to engage in putting together a basic statistical research project. The number of projects completed improved with the addition of an earlier (fourth week of class) initial written commitment to a project idea. Writing on the projects also showed improvement, but this was not specifically analyzed this term.
A separate report on absenteeism in the problematic 8:00 section was published earlier in the term.
As noted in the above report, attendance was problematic for the 8:00 section. The average number of absences by section is noted in the following table. This table, however, provides data only for those students who completed the term. Seven students withdrew from the 8:00 section, two students withdrew from the 9:00 section, and three withdrew from the 10:00 section. Withdrawals from the 8:00 section were dominantly withdrawals due to absences. None of the withdrawn students are included in the average number of absences by section data below.
| Section | Average number of absences |
|---|---|
| 8:00 | 8.29 |
| 9:00 | 7.46 |
| 10:00 | 5.52 |
| Overall | 6.93 |
In statistics a late is a third of an absence. Since I run attendance as a point per day, a third of an absence would be "0.6666..." Thus I actually enter "0.7" making a late technically 30% of an absence. Extremely late (arriving half way through the period) causes a reduction to 50% of a point.
Performance on the final examination by section inversely paralleled the absence table data.
| Section | Average on the final examination |
|---|---|
| 8:00 | 0.66 |
| 9:00 | 0.68 |
| 10:00 | 0.76 |
| Overall | 0.71 |
Note: The overall percentage average of 71% is higher than the 62% average because the 62% is based on an item analysis where an item is either 100% right or 0% wrong. The item analysis looks at each of the forty-nine questions as an all or nothing result. The average on the final, however, is out of 56 possible points where there are single questions worth more than one point and on which a student can obtain partial credit. Questions such as number 13 (a three column table) and 14 (a chart) are examples of multiple point questions.
Although the data suggests a potential connection between attendance and performance on the final examination, an xy scattergraph of individual attendance versus individual final examination scores shows NO correlation. The relationship is random.

Linear regression trend line attendance (not absences) versus performance in course
Note that three students who were still enrolled in the course did not sit for the final examination. These three students were absent, none of these three students contacted the instructor. All three had been absent for the final few weeks of the term, roughly back to spring break.
Although not a direct assessment of learning, grade distributions do have meaning when coupled with in-course assessment that is aligned with the student learning outcomes on the outline. Questions on in-course quizzes and tests consist of questions that can each be mapped back to a student learning outcome on the outline. The bulk of the questions are valued at one point, with certain multiple-entry tables and charts being worth up to five points. Grades are then calculated from the points attained. While this is not matrix-level assessment which permits one to say, "Johnny can do x," I would argue the result is grades that have underlying meaning in terms of student learning. The course grade distribution by section is shown in the following chart.
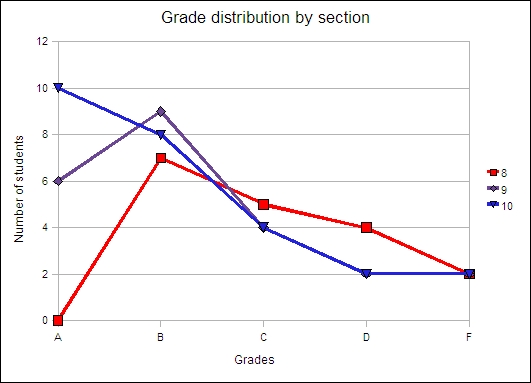
Grade distribution
There appears to be a clear differential in the performance by section where sections later in the day perform better. The factors that may underlay this result are not immediately obvious to this other. A selection effect has been proposed which posits that students who are more organized and self-disciplined registered before less organized students, filling the preferred later sections first. This theory would suggest that the 8:00 section, which fills last, would tend to collect weaker students.
With a debt of gratitude to the SIS programmer, the above theory can be tested. The following table looks at the percentage performance on the final examination against the registration date of the enrolled student.
| Date | Number of students | Average on final |
|---|---|---|
| 11/16/09 | 15 | 0.72 |
| 11/17/09 | 10 | 0.75 |
| 11/18/09 | 8 | 0.71 |
| 11/19/09 | 6 | 0.85 |
| 11/20/09 | 10 | 0.60 |
| 11/23/09 | 1 | 0.80 |
| 01/05/10 | 7 | 0.75 |
| 01/06/10 | 4 | 0.50 |
| 01/11/10 | 1 | 0.75 |
| 01/12/10 | 5 | 0.73 |
| Overall | 67 | 0.71 |
There is no distinct pattern in the data. Where the number of students is less than five, one cannot draw any statistically solid conclusion. The only data point that appears that it might be significantly low is the Friday 20 November set of ten students. This date does include one of the three students who did not sit the final examination, which has a strong impact on the average. One would be hard pressed to argue that there is a pattern whereby earlier registrants performed more strongly as measured by the comprehensive final examination.
The above analysis does not leave much room for a coherent explanation to the poor performance at 8:00, which was a contributing factor to the overall drop in performance.