An evaluation of 38 statistics students in the spring of 2003 yielded an average success rate of 56% on the mathematics program learning outcomes evaluation instrument. An evaluation of 40 statistics students in the spring of 2004 yielded an average success rate of 55% on the mathematics program learning outcomes evaluation instrument. The drop of 1.8% was not statistically significant.
Students continue to experience high rates of success in basic graph reading skills and basic arithmetic calculations. Students were moderately successful with a basic algebraic calculation. Students showed weakness on a question involving vocabulary, inferring mathematical models from graphs, and problem solving within the context of constructive exploration of a mathematical system.
The students were given thirty minutes and permitted to use calculators during the evaluation. The students were all members of MS 150 Statistics, a course with an MS 100 Algebra prerequisite. The course is a mathematical capstone course. Students in the course are likely to be more mathematically able as they are typically computer information systems, health careers, marine science, or business majors.
Students will be able to:
There was no design intent to evaluate each and every outcome, nor to comprehensively evaluate all the facets of each outcome.
The evaluation instrument consisted of eleven multiple choice questions. A web page copy of the evaluation instrument can be viewed at http://www.comfsm.fm/~dleeling/math/progeval/progevalout.html. The actual original file format for the instrument is an OpenOffice.org Write file. This permits better control of page breaks, margins, and formatting. The web page may have differences due to format translation from the OpenOffice file.
The pilot instrument focused on interpreting graphical information with a secondary focus on solving simple word problems. The logic was that post-graduation the bulk of the mathematics that people encounter in life is actually graphical information.
The number of people who actually need to solve quadratic equations as a part of their daily life is starkly few. The bulk of what is taught in a mathematics program is quickly forgotten with no strongly negative impact on the alumni who has forgotten it. Even the faculty of the division of natural sciences and mathematics would be hard pressed to pass an MS 100 College Algebra final examination taken cold.
At the program evaluation level the intent was to look at the life skills implied by the mathematics program student learning outcomes. The eleven items were intended to look at the following outcomes:
This section presumes the reader has a copy of the instrument from http://www.comfsm.fm/~dleeling/math/progeval/progouteval.html in hand while reading this section.
The average success rates by question were as follows:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
Net |
|
|
correct |
14 |
22 |
5 |
34 |
35 |
21 |
34 |
34 |
15 |
23 |
3 |
240 |
|
count |
40 |
40 |
40 |
40 |
40 |
40 |
40 |
40 |
40 |
39 |
40 |
439 |
|
mean |
0.35 |
0.55 |
0.13 |
0.85 |
0.88 |
0.53 |
0.85 |
0.85 |
0.38 |
0.59 |
0.08 |
0.55 |
|
stdev |
0.48 |
0.5 |
0.33 |
0.36 |
0.33 |
0.51 |
0.36 |
0.36 |
0.49 |
0.5 |
0.27 |
0.5 |
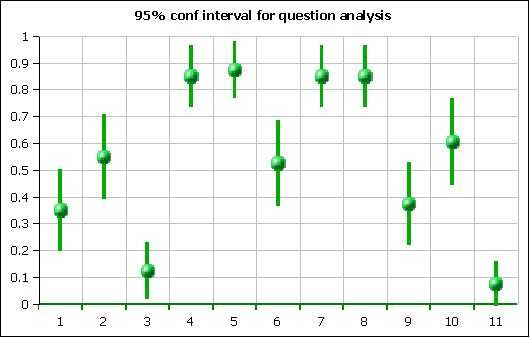
The 95% confidence intervals for these means can be seen in the following chart. The question number is on the horizontal access. The center balls are located at the mean success rate for the question. The vertical lines are the extent of the 95% confidence interval for each mean based on the student's t-distribution.

For a five item question, any 95% confidence interval that touches or crosses 0.2 is not statistically distinguishable from random. For questions with four answers, the random expected result would be 0.25. For questions with three answers, a result of 0.33 would be expected. Questions three and eleven are both statistically significantly below random.
The item analysis is as follows, with the correct answer letter shown in the second row:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
|
c |
b |
b |
d |
a |
b |
a |
b |
c |
d |
b |
|
|
a |
0.5 |
0.15 |
0.7 |
0.03 |
0.88 |
0.33 |
0.85 |
0.1 |
0.33 |
0.03 |
0.7 |
|
b |
0 |
0.55 |
0.13 |
0.13 |
0.08 |
0.53 |
0 |
0.85 |
0.18 |
0.29 |
0.08 |
|
c |
0.35 |
0.03 |
0.13 |
0 |
0.05 |
0.15 |
0.05 |
0.05 |
0.38 |
0 |
0.23 |
|
d |
0.1 |
0.03 |
0.05 |
0.85 |
0 |
0 |
0.1 |
0 |
0.08 |
0.61 |
0 |
|
e |
0.05 |
0.25 |
0 |
0 |
0 |
0 |
0 |
0 |
0.05 |
0.08 |
0 |
Students had difficulty identifying that "six times seven" is the same as "seven times six" as an example of the commutative property. The students more commonly thought that this was the associative property.
Students were only moderately successful at reading a graph in question two, but proved far more competent at reading a graph in question four. The differential in the success rate remains unexplained.
Students experienced extremely low rates of success on question three wherein they had to choose between a linear, quadratic, or square root model for a graph of a falling ball. This suggests students did not come to associate function names with graph shapes during MS 100 College Algebra. For both questions, the mean success rate is statistically significantly below random.
Seventy percent of the students felt that the curved line was best described by a linear model. Unfortunately this may be in part an artifact of studying linear regressions in statistics.
Question eleven could likely only be answered by students who have either taken MS 101 Algebra and Trigonometry or who have studied exponential growth in business and social science classes. Success rates on eleven were below random. Students preferred the linear graph as a model of population doubling. Students clearly do not understand the nature of exponential growth, a key concept in many fields of knowledge.
Question five asks, in words, for students to identify the nature of the correlation seen in the graph – essentially whether the relationship is positive or negative. Statistics students undoubtedly have an advantage at this as it is specifically covered in the course. Statistics students had a high rate of success at this task.
Question six asks a more complex question. Although phrased in words only, the question addresses the existence and sign of the second derivative of the graph. The nature of the change in the rate of change. Despite the complex analysis and synthesis needed to answer this question, half of the students succeeded in answering this question correctly.
Question seven and eight asked the students to perform arithmetic calculations phrased as word problems. Student success rates were very high on both of these questions.
Question nine poses a mathematical puzzle. The student has to know the definition of terms such as perfect square and perfect cube, and then apply that knowledge to solving a simply mathematical puzzle. Although the calculations were well within the capabilities of the students, especially given that they were allowed to use calculators, the confidence interval for the mean success rate was barely above random.
The mathematics of question ten involve calculating the equivalent of a linear equation with a y-intercept. The problem can be solved arithmetically or algebraically. Although the question is only marginally algebraic, it is in simplicity that which one might expect a student to still be able to do years after leaving college.
The absence of college level algebra problems is due to intent and nature of the instrument. The students have not studied for this material. Asking the students to solve a problem involving two equations in two unknowns or finding zeros of a factorisable quadratic are skills for which student could be expected to need to study to complete successfully. The question of what does a student know when they walk down the graduation aisle is the question of what do know and what can they do without having to specifically study. If they can do this simpler problem, then one would hope that they can accomplish more complex tasks with study and knowledge refreshment.
The 61% success rate should appear surprisingly low for students with the mathematical sophistication of a statistics student.
Although the sample sizes make conclusions highly tentative, the program learning outcomes survey instrument data can be "sliced and diced" by a number of factors. More the sake of saving space and maximizing information, much of this data is being presented as cross tabulations. Confidence intervals have not been calculated, the small underlying sample sizes and small differences mean that statistical significance is not always attainable. The data, however, provides a tantalizing glimpse into a world of possibilities and maybes.
The overall mean success rate is shown as sliced by gender and state.
|
State |
female |
male |
Avg |
|
Chuuk |
0.45 |
0.5 |
0.48 |
|
Kosrae |
0.59 |
0.64 |
0.62 |
|
Pohnpei |
0.58 |
0.55 |
0.56 |
|
Yap |
0.57 |
0.45 |
0.51 |
|
Average |
0.56 |
0.54 |
0.55 |
The difference in overall performance between the men and women is certainly not significant. The difference by state between the Kosraens and Chuukese, however, may rise to statistical significance. The interior of the table is plagued by small sample sizes, but suggests a possible underlying weakness in performance for Chuukese females and Yapese males.
Differences by major are also plagued by small sample sizes.
|
Major |
female |
male |
Avg |
|
3rd yr acct |
0.64 |
0.41 |
0.48 |
|
business |
0.61 |
0.65 |
0.64 |
|
computer info sys |
0.56 |
0.52 |
0.54 |
|
hcop |
0.61 |
0.55 |
0.59 |
|
liberal arts |
0.39 |
0.48 |
0.44 |
|
marine science |
0.64 |
0.52 |
0.55 |
|
Average |
0.56 |
0.54 |
0.55 |
The liberal arts major results are probably the most tantalizing in the above. The results suggest that there might be some credence to be given to the stereotyped concept of the liberal arts major as that major for those who are less academically capable.
The data in the table below is the 2004 mean by question minus the 2003 mean by question. The overall drop of 1.8% was not statistically significant.
|
Differences |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
Net |
|
mean |
0.11 |
-0.03 |
-0.06 |
-0.04 |
0.22 |
0.08 |
0.01 |
0.14 |
-0.23 |
-0.12 |
-0.27 |
-0.018 |
|
stdev (se) |
0.1 |
0.11 |
0.08 |
0.08 |
0.09 |
0.11 |
0.08 |
0.09 |
0.11 |
0.11 |
0.09 |
0.03 |
|
low95 |
-0.09 |
-0.25 |
-0.22 |
-0.19 |
0.03 |
-0.15 |
-0.15 |
-0.05 |
-0.45 |
-0.34 |
-0.44 |
-0.08 |
|
high95 |
0.32 |
0.19 |
0.1 |
0.11 |
0.4 |
0.3 |
0.17 |
0.32 |
-0.01 |
0.09 |
-0.09 |
0.05 |
This is the second year in which this instrument has been delivered. Last year was a pilot test. The pilot did lead to modification in the wording of some of the questions and answers to improve clarity. These changes were based on questions asked by students during the spring 2003 evaluation. No student asked questions during this run of the instrument. Some of these changes were noted in last year's report:
During the evaluation questions were raised by students concerning questions two and six. Both of those questions were deemed unclear.
Errors were found in questions five and eight, corrections were put onto the board in each class. Question three included an option to choose a logarithmic model, this was deleted as knowing what a logarithmic function looks like is covered only in the optional elective MS 101 Algebra and Trigonometry course.
The lack of questions from students suggests that the tweaks made improved comprehension and readability. The overall average, however, did not change. One might expect an up tick in the overall scores, but this was not seen. Thus one might surmise that in reality the students did worse than last year by performing the same on a slightly more comprehensible test.
The 95% confidence intervals for the differences in the means between 2003 and 2004 are shown below. Here the value is the 2004 mean minus the 2003 mean. A 95% confidence interval was then calculated. Where the 95% confidence interval crosses the x-axis (y = 0), the change is not statistically significant.
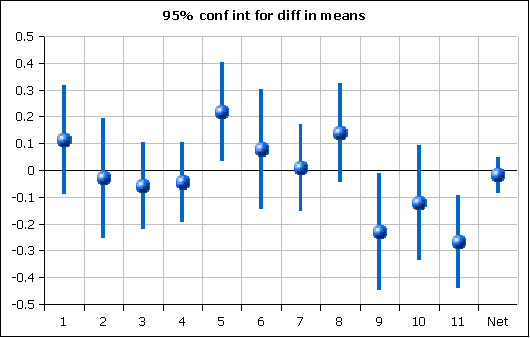
The only questions that saw significant change were five, nine, and eleven. That question five was corrected on the board in 2003 may have been confusing. The improvement seen might be a result of removing that confusion. Both nine and eleven fell by statistically significant amounts.
The 95% confidence interval for the net difference crosses the y = 0 x-axis and hence is not statistically significant at an alpha of 0.05.
Performance on the mathematics program learning outcomes has remained stable over the past year. The implied relative value of the division's grades can be inferred as also being stable. Provided grade distributions have remained stable, there would be no evidence of inflation nor deflation in the relative value of grades awarded by the division.
The 55% overall mean success rate undoubtedly appears low compared to the general expectation of 70%. For two years in a row a very basic instrument has yielded consistent results. This suggests that this is the level at which the students typically perform. Is this unusual for English-as-a-second-language minority students in a community college? Probably not. My guess is that our students perform on par with similar populations elsewhere. This is not, however, actually known. This is the driver for piloting a commercial instrument such as the academic profile instrument that has been discussed in curriculum committee. Such as instrument would allow the institution to compare results to other similar institutions.
All errors are mine, and they are surely many.