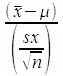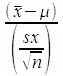MS 150 Quiz 11 • Name:

In the summer of 2007 a pretest in mathematics was given to prejuniors in a UB program. At the end of the summer term a posttest was given. The results are seen in the table.

Pretest Posttest
10 16
5 13
5 5
9 19
10 15
6 19
3 10
8 13
9 11
8 15
5 10
4 12
7 16
6 17
9 18
6 13
8 18
7 8
8 19
11 11
12 12
6 11
7 11
9 17
7 10
11 14
16 18
10 15
6 18
  1. _________ Calculate the sample mean x for the pretest.
  2. _________ Calculate the sample mean x for the posttest.
  3. _________ Are the sample means for the two samples mathematically different?
  4. __________________ What is the p-value? Use the difference of means for paired data TTEST function =TTEST(data_range_x;data_range_y;2;1)to determine the p-value for this paired two sample data.
  5. __________________ Is the difference in the means statistically significant at a risk of a type I error alpha α = 0.05?
  6. __________________ Would we "fail to reject" or "reject" a null hypothesis of no difference in the mean between the pretest and posttest?
  7. __________________ What is the maximum level of confidence we can have that the difference is statistically significant?
Hypothesis Testing
Statistic or ParameterSymbolEquationsOpenOffice
Relationship between confidence level c and alpha α for two-tailed tests 1 − c = α
Calculate t-critical for a two-tailed test tc=TINV(α;df)
Calculate a t-statistic t t 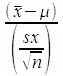t-statistic =(x - μ)/(sx/SQRT(n))
Calculate a two-tailed p-value from a t-statisticp-value = TDIST(ABS(t);df;2)
Calculate a p-value for the difference of the means from two samples of paired samples =TTEST(data_range_x;data_range_y;2;1)
Calculate a p-value for the difference of the means from two independent samples, no presumption that σx = σy =TTEST(data_range_x;data_range_y;2;3)

Statistics • Courses • COMFSM