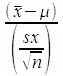
| length/cm |
|---|
| 22 |
| 26 |
| 27 |
| 28 |
| 24 |
| 24 |
| 24 |
| 29 |
| 30 |
| 31 |
| 26 |
| 27 |
| 21 |
| 27 |
| 29 |
| 29 |
| 25 |
| 27 |
| 23 |
| 30 |
A study of the length in centimeters of Cephalopholis argus [English: Peacock hind or blue-spotted grouper, Kosraen: Kalsrik, Mortlockese: Sawei, Mwoakillese: Widir, Pohnpeian: Mwoalusulus, Woleaian: Hali] found in the markets on Pohnpei from January to May 2006 was done by Kevin Rhodes, M. Tupper, Scotty Malakai, Don Jack, Clement Wichilmel, Richard Ben, and Kirino and Anson Olpet. The data is based loosely on this work. For the purposes of this quiz, consider that the average length for a population of blue-spotted groupers which has not been overharvested is μ = 30 centimeters. In other words, 30 cm is the mean for a healthy grouper population.
Consider a null hypothesis for which H0: μ = 30
and an alternate hypothesis for which H1: μ ≠ 30
Run a hypothesis test at a risk of a type I error α = 0.05
| Hypothesis Testing | |||
|---|---|---|---|
| Statistic or Parameter | Symbol | Equations | OpenOffice |
| Relationship between confidence level c and alpha α for two-tailed tests | 1 − c = α | ||
| Calculate t-critical for a two-tailed test | tc | =TINV(α;df) | |
| Calculate a t-statistic t | t | 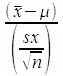 |
=(x - μ)/(sx/SQRT(n)) |
| Calculate a two-tailed p-value from a t-statistic | p-value | = TDIST(ABS(t);df;2) | |
| Calculate a p-value for the difference of the means from two samples of paired samples | =TTEST(data_range_x;data_range_y;2;1) | ||
| Calculate a p-value for the difference of the means from two independent samples, no presumption that σx = σy | =TTEST(data_range_x;data_range_y;2;3) | ||