MS 150 Statistics fx summer 2007 • Name:
On Sunday 08 July 2007 the
Honolulu Advertiser ran an
article
covering the rising number of Micronesians using Hawaii's homeless shelters. The number soared by nearly three times between 2001 and 2006, and Micronesians now make up more than 20 percent of the state's total homeless population.
Micronesian homeless shelter users
| Year | Number |
|---|
| 2001 | 286 |
| 2002 | 316 |
| 2003 | 554 |
| 2004 | 463 |
| 2005 | 513 |
| 2006 | 736 |
Part I: Basic Statistics
Use the number of Micronesians in homeless shelters in Hawaii ("number of shelter users") for the following calculations. Do not use the year data!
- _________ What level of measurement is the number of shelter users data?
- _________ Determine the sample size n.
- _________ Calculate the sample mean
x.
- _________ Determine the median.
- _________ Determine the mode.
- _________ Determine the minimum.
- _________ Determine the maximum.
- _________ Calculate the range.
- _________ Calculate the sample standard deviation sx.
- _________ Calculate the sample Coefficient of Variation.
- _________ Determine the class width. Use three bins (classes or intervals). Note that the number of bins is three!
- Fill in the following table with the class upper limits in the first column, the frequencies in the second column, and the relative frequencies in the third column
| Bins (x) | Frequency f | RF p(x) |
|---|
| _________ | _________ | _________ |
| _________ | _________ | _________ |
| _________ | _________ | _________ |
|
Sums: | _________ | _________ |
- Sketch a histogram of the relative frequency data.
- __________________ What is the shape of the distribution?
- __________________ Using the sample mean x and the sample standard deviation sx calculated above, determine the z-score for the 736 Micronesian shelter users in 2006.
- _________ Is the z-score for 736 Micronesian shelter users in 2006 an ordinary or extraordinary value?
- _________ Calculate the standard error of the sample mean for the number of Micronesian shelter users.
- _________ Find tcritical for a confidence level of 95% for the number of Micronesian shelter users.
- _________ Determine the margin of error E for the sample mean.
- Write out the 95% confidence interval for the population mean number of shelter users:
_________ ≤ μ ≤ _________
Part II: Hypothesis Testing using the t-test
The following data is also from the Honolulu Advertiser article cited above. This section examines whether there is pairwise difference in the number of shelter users based on island ethnicity for the six years between 2001 and 2006.
Homeless shelter users
| Year | Hawaiians (x) | Micronesians (y) |
|---|
| 2001 | 1117 | 286 |
| 2002 | 1039 | 316 |
| 2003 | 864 | 554 |
| 2004 | 857 | 463 |
| 2005 | 756 | 513 |
| 2006 | 744 | 736 |
- __________________ Use the paired TTEST function =TTEST(data_range_x;data_range_y;2;1)to determine the p-value for this paired two sample data.
- __________________ Is the pairwise difference in the number of Hawaiians and the number of Micronesians statistically significant at a risk of a type I error alpha α = 0.05?
- __________________ Would we fail to reject or reject a hypothesis of no mean pairwise difference in the numbers in homeless shelters in Hawaii based on ethnicity?
- __________________ What is the maximum level of confidence we can have that the pairwise difference is statistically significant?
Part III: Linear Regression
Micronesian shelter Users
| Year | Number |
|---|
| 01 | 286 |
| 02 | 316 |
| 03 | 554 |
| 04 | 463 |
| 05 | 513 |
| 06 | 736 |
The data in this section examines whether there is a trend in the number of Micronesian entering homeless shelters from 2001 to 2006. Note that only the last two digits of the year are being used in this section.
- _________ Calculate the slope of the best fit (least squares) line.
- _________ Calculate the y-intercept of the best fit (least squares) line.
- _________ Is the correlation positive, negative, or neutral?
- _________ Calculate the predicted number of Micronesians in homeless shelters in Hawaii in 07.
- _________ Calculate the year in which 1000 Micronesians are predicted to be entering homeless shelters in Hawaii.
- _________ Calculate the linear correlation coefficient r for the data.
- _________ Is the correlation none, low, moderate, high, or perfect?
The Honolulu Advertiser article is based on independent research by Michael D. Ullman. As always statistics can be and are deployed to support particular positions. This data is likely being used by the state of Hawaii to seek reimbursement for Compact impact. The article makes an important note at the start of the article, "[Micronesians] now make up more than 20% of the state's total homeless population. Given the data above, this suggests that 20% are Hawaiian and the 60% majority of the homeless are neither Hawaiian nor Micronesian.
Tables of Formulas and OpenOffice Calc functions
| Basic Statistics |
| Statistic or Parameter | Symbol | Equations | OpenOffice |
|---|
| Square root | | | =SQRT(number) |
| Sample standard deviation | sx or s | | =STDEV(data) |
| Sample Coefficient of Variation | CV |
sx/x |
=STDEV(data)/AVERAGE(data) |
| Confidence interval statistics |
|---|
| Statistic or Parameter | Symbol | Equations | OpenOffice |
| Degrees of freedom | df | = n-1 | =COUNT(data)-1 |
| Find a tc value from a confidence level c |
tc | | =TINV(1-c;df) |
| Calculate the standard error of the mean | | | =sx/SQRT(n) |
| Calculate a margin of error for the mean E for n < 30 using sx. Should also be used for n ≥ 30. |
E |
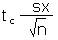 |
=tc*sx/SQRT(n) |
| Calculate a confidence interval for a population mean µ from a sample mean x and an error tolerance E |
x - E ≤ µ ≤ x + E |
| Hypothesis Testing |
|---|
| Relationship between confidence level c and alpha α for two-tailed tests |
1 − c = α | |
| Calculate t-critical for a two-tailed test |
tc | | =TINV(α;df) |
| Calculate a t-statistic |
t |
 |
=(x - µ)/(sx/SQRT(n)) |
| Calculate a two-tailed p-value from a t-statistic | p-value | |
= TDIST(ABS(t);df;2) |
| Calculate a p-value for the difference of the means from two samples of paired samples | =TTEST(data_range_x;data_range_y;2;1) |
| Calculate a p-value for the difference of the means from two independent samples, no presumption that σx = σy | =TTEST(data_range_x;data_range_y;2;3) |
| Linear Regression Statistics |
| Statistic or Parameter | Symbol | Equations | OpenOffice |
| Slope | b | | =SLOPE(y data; x data) |
| Intercept | a | | =INTERCEPT(y data; x data) |
| Correlation | r | | =CORREL(y data; x data) |
| Coefficient of Determination | r2 | |
=(CORREL(y data; x data))^2 |
