Statistics spring 2007 quiz three 9.2

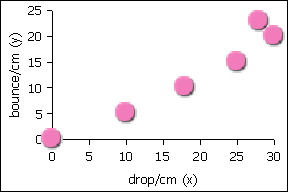
q03 (6K)

______________ Does the relationship appear to be linear, non-linear, or random?
______________ Determine the slope of the linear regression for the data.
______________ Determine the y-intercept of the linear regression for the data.
______________ Determine the correlation coefficient r.
______________ Is the correlation positive or negative?
______________ Is the correlation none, weak, moderate, strong, or perfect?
______________ Determine the coefficient of determination.
______________ What percent in the variation in the drop "explains" the variation in the bounce?
______________ Use the slope and intercept above to calculate the predicted bounce for a drop of 21 centimeters.
______________ Use the slope and intercept to solve for the predicted drop that will produce a bounce of 7 cm.
______________ For the following example, presume that the linear relationship holds beyond the maximum x-value. Use the slope and intercept above to calculate the predicted bounce for a drop of 260 centimeters.
______________ Is there any one data point that looks like it might be an error?
______________ Which specific drop and bounce data point, if any, looks like it might be in error?
If you picked a point as being an error, why did you pick that point?

Linear Regression Functions
Statistic or Parameter	Math symbol	Stat symbol	OpenOffice
Slope	m	b	=slope(y-data;x-data)
Intercept	b	a	=intercept(y-data;x-data)
Correlation	r		=correl(y-data;x-data)
Coefficient of Determination	r²		=(correl(y-data;x-data))^2