MS 150 Statistics fx spring 2007 • Name:
Glaciers of Iceland
| Glacier name | Rate/m |
|---|
| Breidamerkurjökull | 48 |
| Breidamerkurjökull | 108 |
| Breidamerkurjökull | 18 |
| Falljökull | 18 |
| Fjallsjökull | 10 |
| Fjallsjökull | 18 |
| Fjallsjökull | 16 |
| Fláajökull | 22 |
| Gígjökull | 75 |
| Hrútárjökull | 6 |
| Kverkjökull | 42 |
| Kvíárjökull | 3 |
| Morsárjökull | 9 |
| Múlajökull | 48 |
| Nathagajökull | 8 |
| Öldufellsjökull | 88 |
| Sátujökull | 93 |
| Síðujökull | 44 |
| Skaftafellsjökull | 4 |
| Skeiðarárjökull | 27 |
| Skeiðarárjökull | 9 |
| Skeiðarárjökull | 69 |
| Skeiðarárjökull | 21 |
| Svínafellsjökull | 3 |
| Tungnaárjökull | 23 |
Part I: Basic Statistics
Glaciers are giant sheets of ice and snow that flow like a vast frozen river down high latitude and high altitude mountain valleys. Glaciers move very slowly, typically only a few decimeters per year. Each winter snowfall on the glacier basin replenishes the glacier. At the bottom of the glacier the ice sheet either melts as water or calves off into the ocean. The result is a balance where the glacier remains the same length over long periods of time. Global warming, however, is melting glaciers faster than winter snows can rebuild the glacier. Glaciers exhibit this most by increased melting on the bottom or front of the glacier. The glacier gets shorter with each passing year. The data in the table is the average annual retreat of the glacier front for glaciers in Iceland. Some glaciers have more than one "tongue" and measurements are made for each tongue. Globally, glacial melting is a contributor to sea level rise. While places like Iceland lose their glaciers, places like Micronesia lose their atolls. The data is also available in a data sheet to save you retyping the data.
For the annual retreat rate in meters for the glaciers of Iceland data given in the table (to avoid using negative numbers, this section uses positive numbers for the amount of retreat of the glacier front in meters):
- _________ What level of measurement is the data?
- _________ Determine the sample size n.
- _________ Calculate the sample mean
x.
- _________ Determine the median.
- _________ Determine the mode.
- _________ Determine the minimum.
- _________ Determine the maximum.
- _________ Calculate the range.
- _________ Calculate the sample standard deviation sx.
- _________ Calculate the sample Coefficient of Variation.
- _________ Determine the class width. Use seven bins (classes or intervals). Note that the number of bins is seven!
- Fill in the following table with the class upper limits in the first column, the frequencies in the second column, and the relative frequencies in the third column
| Bins | Frequency | RF p(x) |
|---|
| _________ | _________ | _________ |
| _________ | _________ | _________ |
| _________ | _________ | _________ |
| _________ | _________ | _________ |
| _________ | _________ | _________ |
| _________ | _________ | _________ |
| _________ | _________ | _________ |
|
Sums: | _________ | _________ |
- Sketch a histogram of the relative frequency data.
- __________________ What is the shape of the distribution?
- _________ What is the standard error of the mean?
- _________ Find tcritical for a confidence level of 95% for the data in the table.
- _________ Determine the margin of error E for the 95% confidence interval for the data in the table.
Write out the 95% confidence interval for the population mean retreat rate:
_________ ≤ μ ≤ _________
- _________ Is a population mean retreat rate of zero a possible population mean based on the 95% confidence interval?
- A hypothesis test for whether the glaciers are actually retreating would test the null hypothesis where the population mean retreat rate is zero (the glaciers are not provably melting) against an alternate hypothesis where the mean retreat rate is not zero:
H0: μ = 0 meters per year rate of retreat
H1: μ ≠ 0 meters per year rate of retreat
__________________ Would we reject the null hypothesis or fail to reject the null hypothesis?
- _________ Calculate the t-statistic using the sample mean and sample standard deviation from the data in the table. Use a population mean of μ = 0.
__________________ Use the t-statistic to find the p-value. Remember to increase the decimal places in OpenOffice Calc. Use six decimal places.
__________________ What is the maximum level of confidence we can have that the rate of glacier retreat is not zero (that the glaciers are really retreating, shrinking in length).
Part II: Hypothesis Testing using the t-test
The following data is also glacier retreat rate data from glaciers in Iceland. Because this data includes glaciers that retreated and glaciers that grew longer, the data includes positive and negative measurements. In this section negative numbers are the distance in meters the glacier retreated (shrank, got smaller) while the positive numbers are the distance in meters that the glacier advanced (grew longer). The paired data is measurements for individual glaciers taken in 1996 and four years later in 2000.
Glacier front movement data
| Glacier | 1996 | 2000 |
|---|
| Breidamerkurjökull | -20 | -5 |
| Breidamerkurjökull | -45 | -40 |
| Falljökull | 1 | -37 |
| Fjallsjökull | 23 | -63 |
| Fjallsjökull | -10 | -5 |
| Fjallsjökull | 12 | -20 |
| Fláajökull | 10 | -53 |
| Gígjökull | 10 | -136 |
| Hrútárjökull | -20 | 0 |
| Kaldaklofsfjöll | 38 | 0 |
| Kvíárjökull | 4 | 0 |
| Morsárjökull | -31 | -14 |
| Múlajökull | -8 | -50 |
| Nathagajökull | -5 | -5 |
| Sátujökull | -200 | -51 |
| Skaftafellsjökull | 51 | -70 |
| Skeiðarárjökull | -33 | -1 |
| Skeiðarárjökull | -31 | -10 |
| Skeiðarárjökull | -4 | -14 |
| Skeiðarárjökull | -13 | -110 |
| Svínafellsjökull | 5 | -5 |
| Tungnaárjökull | -53 | -19 |
- __________________ What is the mean glacier movement in meters for 1996?
- __________________ What is the mean glacier movement in meters for 2000?
- __________________ Use the TTEST function to determine the p-value for this paired two sample data.
- __________________ What is the maximum level of confidence we can have that the mean glacier movements are different between 1996 and 2000?
- __________________ Are the mean rates of movement for the glaciers in 1996 and 2000 statistically significantly different at an alpha of α = 0.05?
- For a hypothesis test on the paired mean difference μdifference where:
H0: μdifference = 0
H1: μdifference ≠ 0
Do we «fail to reject the null hypothesis» or «reject the null hypothesis» at an alpha α = 0.05?
Part III: Linear Regression
Skeiðarárjökull movement
| Year | Movement/meters |
|---|
| 1996 | -13 |
| 1997 | -38 |
| 1998 | -35 |
| 1999 | -150 |
| 2000 | -110 |
The data in this section examines whether there is a trend in the retreat rate for the Skeiðarárjökull glacier front. Note that this section the numbers are the retreat rate, a velocity or speed of retreat in meters per year. Negative numbers represent the retreat, shrinking of the length of the glacier.
- _________ Calculate the slope of the best fit (least squares) line.
- _________ Calculate the y-intercept of the best fit (least squares) line.
- _________ Is the correlation positive, negative, or neutral?
- _________ Use the equation of the best fit line to calculate the predicted retreat rate in 2007.
- _________ Use the inverse of the best fit line to calculate the year in which the retreat rate was zero.
- _________ Calculate the linear correlation coefficient r for the data.
- _________ Is the correlation none, low, moderate, high, or perfect?
- _________ Calculate the coefficient of determination.
- _________ What percent of the variation in the year explains the variation in the retreat rate?
- The retreat rate is the speed at which the glaciers are retreating. Is this rate of retreat increasing with each passing year or decreasing with each pass year? That is, are the glaciers eventually going to get longer or are they going to shrink at a faster and faster rate of shrinking?
The data on this final is based on actual data from the World Glacier Monitoring Service. With four major reports on climate change being released this year, all of which indicate almost catastrophic changes for atoll dwellers over the next seventy years, it seemed appropriate to focus on climate change this term.
Tables of Formulas and OpenOffice Calc functions
| Basic Statistics |
| Statistic or Parameter | Symbol | Equations | OpenOffice |
|---|
| Square root | | | =SQRT(number) |
| Sample standard deviation | sx or s | | =STDEV(data) |
| Sample Coefficient of Variation | CV |
sx/x |
=STDEV(data)/AVERAGE(data) |
| Confidence interval statistics |
|---|
| Statistic or Parameter | Symbol | Equations | OpenOffice |
| Degrees of freedom | df | = n-1 | =COUNT(data)-1 |
| Find a tc value from a confidence level c |
tc | | =TINV(1-c;df) |
| Calculate the standard error of the mean | | | =sx/SQRT(n) |
| Calculate a margin of error for the mean E for n < 30 using sx. Should also be used for n ≥ 30. |
E |
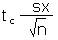 |
=tc*sx/SQRT(n) |
| Calculate a confidence interval for a population mean µ from a sample mean x and an error tolerance E |
x - E ≤ µ ≤ x + E |
| Hypothesis Testing |
|---|
| Relationship between confidence level c and alpha α for two-tailed tests |
1 − c = α | |
| Calculate t-critical for a two-tailed test |
tc | | =TINV(α;df) |
| Calculate a t-statistic |
t |
 |
=(x - µ)/(sx/SQRT(n)) |
| Calculate a two-tailed p-value from a t-statistic | p-value | |
= TDIST(ABS(t);df;2) |
| Calculate a p-value for the difference of the means from two samples of paired samples | =TTEST(data_range_x;data_range_y;2;1) |
| Calculate a p-value for the difference of the means from two independent samples, no presumption that σx = σy | =TTEST(data_range_x;data_range_y;2;3) |
| Linear Regression Statistics |
| Statistic or Parameter | Symbol | Equations | OpenOffice |
| Slope | b | | =SLOPE(y data; x data) |
| Intercept | a | | =INTERCEPT(y data; x data) |
| Correlation | r | | =CORREL(y data; x data) |
| Coefficient of Determination | r2 | |
=(CORREL(y data; x data))^2 |
