Statistics Quiz 07 fall 2006 7.3a • Name:

1. The figure below depicts six curves:
   
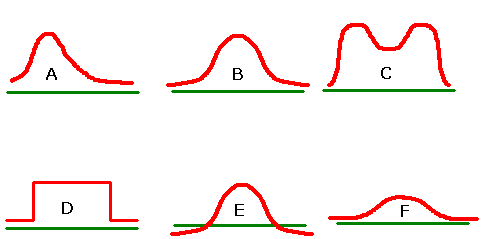
   Which, if any, of the curves in the figure above look(s) like a normal curve? If the curve is a NOT normal curve, tell why.
2. 1. For the following curves A, B, and C determine the mean µ and the standard deviation σ:
   

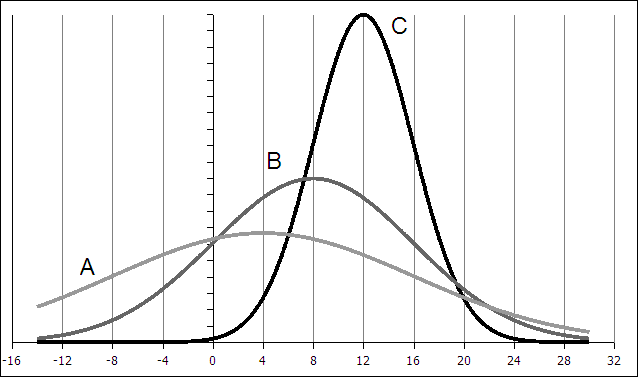
   Curve	Mean µ	standard deviation σ
   A
   B
   C

3. On the eighth of October I joggled 18 laps of the track. I had a mean lap time of µ = 2.5 minutes with a standard deviation of σ = 0.25 minutes. My lap times were normally distributed.

1. p(x ≤ 2.5 minutes) = __________ What is the probability a lap had a time of 2.5 minutes or less?
2. p(x ≤ 2.25) = __________ What is the probability that a lap was 2.25 minutes or less?
3. __________ Of the 18 laps, how many were 2.25 minutes or less?
4. p(x ≥ 2.67) = __________ What is the probability that a lap was 2.67 minutes or more? Use OpenOffice to answer this!
5. p(2.33 ≤ x ≤ 2.67) = __________ What is the probability that a lap was more than 2.33 and less than 2.67? Use OpenOffice to answer this!
6. __________How many of the laps were between 2.33 and 2.67 minutes? Use OpenOffice to answer this!

Normal Statistics
Calculate a z value from an x	z	=	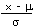=STANDARDIZE(x;µ;σ)
Calculate an x value from a z	x	= z σ + µ	=z*σ+µ
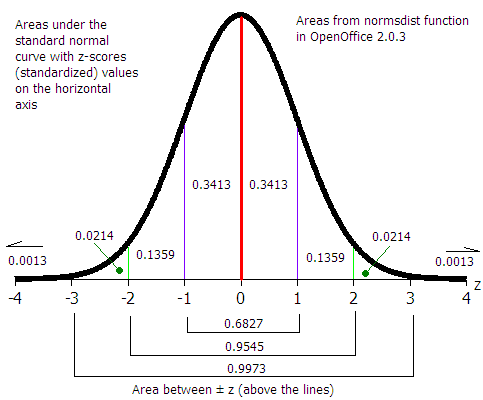
Find a probability p(x) from a z value where the probability p is the area to the left of z.			=NORMSDIST(z)

Statistics • Courses • COMFSM