MS 150 Statistics fx spring 2006 • Name:
b.p.
| Sys. |
|---|
| 96 |
| 113 |
| 114 |
| 116 |
| 118 |
| 119 |
| 120 |
| 126 |
| 129 |
| 129 |
| 130 |
| 133 |
| 134 |
| 135 |
| 135 |
| 135 |
| 138 |
| 145 |
| 148 |
| 148 |
| 151 |
| 175 |
Part I: Basic Statistics
Systolic blood pressures were measured for twenty-two caffeine consuming students in exercise sport science courses this spring. The systolic blood pressure data is in the table and in an on line data sheet. Systolic blood pressure is the blood pressure generated by the contraction of the heart. Normal human systolic blood pressure is usually 120.
Data sheet
For the systolic blood pressure data given in the table:
- _________ What level of measurement is the systolic blood pressure data?
- _________ Determine the sample size n.
- _________ Calculate the sample mean
x.
- _________ Determine the median.
- _________ Determine the mode.
- _________ Determine the minimum.
- _________ Determine the maximum.
- _________ Calculate the range.
- _________ Calculate the sample standard deviation sx.
- _________ Calculate the sample Coefficient of Variation.
- _________ Determine the class width. Use five bins (classes or intervals)
- Fill in the following table with the class upper limits in the first column, the frequencies in the second column, and the relative frequencies in the third column
| Bins | Frequency | Relative Frequency f/n |
|---|
| _________ | _________ | _________ |
| _________ | _________ | _________ |
| _________ | _________ | _________ |
| _________ | _________ | _________ |
| _________ | _________ | _________ |
|
Sums: | _________ | _________ |
- Sketch a histogram of the relative frequency data on the bottom of page three.
- __________________ What is the shape of the distribution?
- __________________ What is the probability of rolling a four on an eight-sided die that has faces numbered from one to eight?
Part II: Estimated mean from a distribution
Systolic blood pressure measurements were made on 48 drug free students. The results are recorded in the table below.
| Bin upper limit | Freq f | Rel Freq | _______ |
|---|
| 106.6 | 7 | 0.15 | ______ |
| 116.2 | 12 | 0.25 | ______ |
| 125.8 | 12 | 0.25 | ______ |
| 135.4 | 13 | 0.27 | ______ |
| 145 | 4 | 0.08 | ______ |
| | 48 | 1.00 | ________ |
- __________________ What the the estimated mean systolic blood pressure for these 48 drug-free students?
Part III: Confidence Intervals
A sample size n of eight students who consume caffeinated beverages but who do not use any other drugs had a sample mean x systolic blood pressure of 128.63 with a sample standard deviation sx of 19.21. Construct a 95% confidence interval for the population mean µ systolic blood pressure for these eight caffeine users. Note that n is less than 30.
- ____________ What would be the point estimate for the population mean µ for all students who drink caffeinated beverages on campus?
- df = __________ Find the number of degrees of freedom.
- tc = __________ Find tcritical.
- E = _______________ Find the error tolerance E.
- The 95% confidence interval for the population mean caffeine users systolic blood pressure µ is:
____________ ≤ µ ≤ ____________
- __________ The drug free population mean µ systolic blood pressure for students at the College of Micronesia-FSM is 119.41. Is a population mean systolic blood pressure of 119.41 a possible mean systolic blood pressure for the caffeine using students based on the 95% confidence interval?
Part IV: Hypothesis Testing
Betelnut contains the simulant arecoline, coffee and cola drinks contain the stimulant caffeine, tobacco contains the stimulant nicotine. A group of students who do not chew betelnut, consume caffeinated beverages, smoke, nor chew tobacco had a population mean systolic blood pressure µ of 119.41. There are a number of students who consume all three stimulants, often at the same time. A sample size n of seven students who chew betelnut with tobacco and consume caffeinated beverages had a sample mean x systolic blood pressure of 129.29 with a sample standard deviation sx of 7.95. Could this sample of seven students include a population mean systolic blood pressure µ of 119.41? Test the hypothesis that the population mean systolic blood pressure for the sample could or could not be 119.41.
Use an alpha of α = 0.05 for the hypothesis test.
- ________________________________________ Write the null hypothesis in formal statistical format.
- ________________________________________ Write the alternate hypothesis in formal statistical format.
- α = __________ Write down the level of significance alpha.
- tc = __________ Determine tcritical.
- t = __________ Calculate the t-statistic.
- p = __________ Determine the p-value using the t-distribution.
- __________ What is the largest confidence interval c for which this difference is statistically significant?
- ________________________________________ Would we reject the null hypothesis or fail to reject the null hypothesis that the sample mean is statistically significantly different from the population mean at a 5% level of significance?
- __________ If we reject the null hypothesis, what is the risk of a type I error based on the p-value?
- __________ Do the students using all three stimulants have a statistically significantly higher systolic blood pressure than the drug-free students?
- __________ Is high blood pressure good for your body?
Part V: Linear Regression
Age vs systolic
| Age/years | Systolic |
|---|
| 18 | 109 |
| 18 | 113 |
| 19 | 145 |
| 19 | 117 |
| 20 | 106 |
| 20 | 105 |
| 20 | 163 |
| 20 | 119 |
| 20 | 132 |
| 20 | 120 |
| 20 | 134 |
| 20 | 146 |
| 21 | 116 |
| 21 | 123 |
| 21 | 101 |
| 22 | 145 |
| 22 | 101 |
| 23 | 129 |
| 23 | 133 |
| 25 | 126 |
| 29 | 135 |
The data in this section examines whether there is a trend in the systolic blood pressure for students with age.
- _________ Calculate the slope of the best fit (least squares) line for the data.
- _________ Calculate the y-intercept of the best fit (least squares) line.
- _________ Is the correlation positive, negative, or neutral?
- _________ Use the equation of the best fit line to calculate the predicted systolic blood pressure for a 24 year old student.
- _________ Use the inverse of the best fit line to calculate the predicted age for a systolic blood pressure of 140.
- _________ Calculate the linear correlation coefficient r for the data.
- _________ Is the correlation none, low, moderate, high, or perfect?
- _________ Calculate the coefficient of determination.
- _________ What percent of the variation in the age data explains the variation in the blood pressure data?
- _________ Can we use a linear regression to predict blood pressure from age?
- Why or why not?
Tables of Formulas and Excel functions
| Basic Statistics |
| Statistic or Parameter | Symbol | Equations | Excel |
|---|
| Square root | | | =SQRT(number) |
| Sample standard deviation | sx or s | | =STDEV(data) |
| Sample Coefficient of Variation | CV |
sx/x |
=STDEV(data)/AVERAGE(data) |
| Confidence interval statistics |
|---|
| Statistic or Parameter | Symbol | Equations | Excel |
| Degrees of freedom | df | = n-1 | =COUNT(data)-1 |
| Find a zc value from a confidence level c |
zc | | =ABS(NORMSINV((1-c)/2)) |
| Find a tc value from a confidence level c |
tc | | =TINV(1-c,df) |
| Calculate an error tolerance E of a mean for n < 30 using sx. Should also be used for n ≥ 30. |
E |
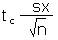 |
=tc*sx/SQRT(n) |
| Calculate a confidence interval for a population mean µ from a sample mean x and an error tolerance E |
|
x - E ≤ µ ≤ x + E |
| Hypothesis Testing |
|---|
| Calculate t-critical for a two-tailed test |
tc | | =TINV(α,df) |
| Calculate a t-statistic |
t |
 |
=(x - µ)/(sx/SQRT(n)) |
| Calculate a two-tailed p-value from a t-statistic | p | |
= TDIST(ABS(t),df,2) |
| Linear Regression Statistics |
| Statistic or Parameter | Symbol | Equations | Excel |
| Slope | b | | =SLOPE(y data, x data) |
| Intercept | a | | =INTERCEPT(y data, x data) |
| Correlation | r | | =CORREL(y data, x data) |
| Coefficient of Determination | r2 | |
=(CORREL(y data, x data))^2 |
