Purposes
|
Set Up
|
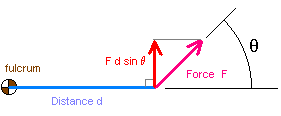
Levers utilize torque to assist us in lifting or moving objects. Torque is the cross product between a force and the distance of the force from a fulcrum (the central point about which the system turns). The cross product takes only the component of the force acting perpendicular to the distance. Using trigonometry the torque is defined as:
Torque = Force × Distance to fulcrum × sin (θ)
Remember that work was also force multiplied by the distance, but it was the dot product and used the cosine of the angle between the force and distance: force × distance × cos(θ).
In this laboratory the force will be perpendicular (90°) to the distance. The sine of 90° is one, therefore the torque will be:
Torque = Force × Distance to fulcrum × sin (θ)
Torque = Force × Distance to fulcrum × sin (90°)
Torque = Force × Distance to fulcrum × 1
Torque = Force × Distance to fulcrum
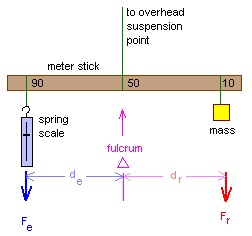
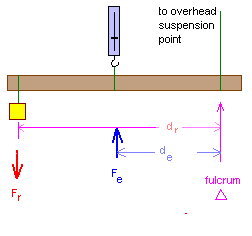
In a class one lever the fulcrum is between the force of the resistance (Fr) and the force of the effort (Fe). In a class one lever the force of the effort (Fe) multiplied by the distance of the effort from the fulcrum (de) is equal to the force of the resistance (Fr) multiplied by the distance of the resistance from the fulcrum (dr). The effort and the resistance are on opposite sides of the fulcrum. Pliers are an example of a class one lever.
In the diagram, the mass provides the resistance, the spring scale measures our efforts. The spring scale is calibrated in grams. Grams are not a unit of force per se, but in this laboratory we will use the term gram-force" as the force exerted on one gram at the Earth's surface by the acceleration of gravity. One "gram-force" will be equivalent to 980 cm/sec2 (dynes).
For the diagram: Fe × de = Fr × dr
Mechanical advantage = Fr/Fe
| Fe | de | Fe × de | Fr | dr | Fr × dr | Fede = Frdr? | M.A. |
|---|---|---|---|---|---|---|---|
| ________ | ________ | ________ | ________ | ________ | ________ | Yes | No | ________ |
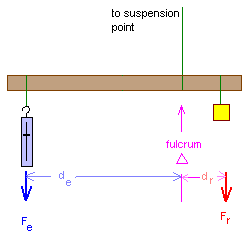
For the diagram: Fe × de = Fr × dr
Mechanical advantage = Fr/Fe
| Fe | de | Fe × de | Fr | dr | Fr × dr | Fede = Frdr? | M.A. |
|---|---|---|---|---|---|---|---|
| ________ | ________ | ________ | ________ | ________ | ________ | Yes | No | ________ |
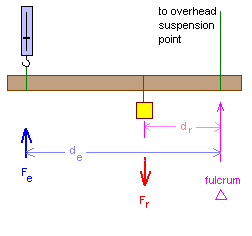
In a class two lever the resistance is between the force of the effort and the fulcrum. In a class two lever the force of the effort multiplied by the distance of the effort from the fulcrum is opposite and equal to the force of the resistance multiplied by the distance of the resistance from the fulcrum. The effort and the resistance are on the same side of the fulcrum but point in opposite directions.
The effort distance (also sometimes called the "effort arm") is longer than the resistance distance.
Wheelbarrows and giant taro digging poles (when we push up on the pole) are examples of class two levers.
Note that our choice of down as being positive in the first part of the lab means that up is now negative in this section. So Fe is a negative force. Write Fe as negative in the table and then -Fe × de will be positive.
For the diagram: -Fe × de = Fr × dr
Mechanical advantage = |Fr/Fe | where | means "absolute
value." Mechanical advantage is always positive.
| Fe | de | -Fe × de | Fr | dr | Fr × dr | -Fede = Frdr? | M.A. |
|---|---|---|---|---|---|---|---|
| ________ | ________ | ________ | ________ | ________ | ________ | Yes | No | ________ |
In a class three lever the resistance is between the force of the effort and the fulcrum. In a class three lever the force of the effort multiplied by the distance of the effort from the fulcrum is opposite and equal to the force of the resistance multiplied by the distance of the resistance from the fulcrum. The effort and the resistance are on the same side of the fulcrum but point in opposite directions.
The effort distance (also sometimes called the "effort arm") is shorter than the resistance distance.
For the diagram: -Fe × de = Fr × dr
Mechanical advantage = |Fr/Fe | where | means "absolute
value." Mechanical advantage is always positive.
| Fe | de | -Fe × de | Fr | dr | Fr × dr | -Fede = Frdr? | M.A. |
|---|---|---|---|---|---|---|---|
| ________ | ________ | ________ | ________ | ________ | ________ | Yes | No | ________ |
In the class III lever the mechanical advantage might be called a mechanical disadvantage. Why? (Suggestion: Consider the force of the effort, is it less than the force of the resistance or more than the force of the resistance?)
Note that the human lower arm is a third class lever: the bicep, attached just below the elbow, can be used to lift a weight being held in the hand at the end of the lower arm.
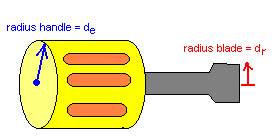
A screwdriver is actually a form of lever where a handle with a large radius provides a mechanical advantage in turning a blade with a smaller radius. All sorts of circular devices make use of this form of mechanical advantage. Circular water valve handles, tire irons, socket wrenches, monkey wrenches, and many other items utilize this time of circular lever.
Measure the radius of the handle on a screwdriver and then measure the radius of the blade. Calculate the mechanical advantage from de/dr.
Note that the mechanical advantage to a circular device is de/dr while the mech. adv. for a lever was Fr/Fe. Note that the seeming "flip-flop" of the fraction is not a mistake.
Consider that Fe × de = Fr × dr. Cross dividing by Fe and dr yields:
de = Fr -- -- = mechanical advantage dr Fe
SC 130 Home page
Lee Ling's Courses Home Page
![]() To COM-FSM Home Page
To COM-FSM Home Page