This page designed using Microsoft Frontpage 97 and tested only on Microsoft Internet Explorer 3.0.
This is an internal report in the continuing follow-up to the experimental Conceptual Approach mathematics Dana Lee Ling taught in the Fall of 1996 out here. The results are encouraging. I would caution that the use of the term "Conceptual Approach" is strictly of my own invention. I would guess that the term has been used by others in approaches that likely differ from what I did. My use of the term does not imply a connection to any other program that might be using the same terminology.
– Dana Lee Ling, June 1997.
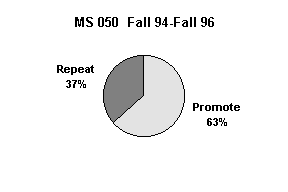
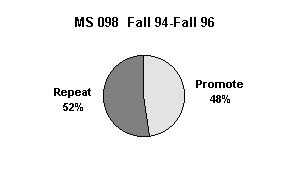
The mathematics department at the College of Micronesia–FSM had historically experienced differential rates of student success in MS 050 PreAlgebra and MS 098 Transition to Algebra. Students appeared to be succeeding in MS 050 and then failing in MS 098. Students who fail a course then repeat that same course at the College.


There was also the sense in the department that once a student does repeat a class, the student tends to continue to fail the class in subsequent attempts. Anecdotal accounts indicated that these multiple-repeat students were unprepared for the class they were repeatedly failing, although these same students had passed the prerequisite course.
In the Fall of 1996 the College ran a single experimental section of MS 050 PreAlgebra that used a non-traditional curriculum for a remedial college math course. The experimental section, referred to as the Conceptual Approach, was built on the premise that the students who come to the College are not a blank slate. The premise was that students come with a confused, incomplete, and faulty knowledge of mathematics. The drill and practice approach of the extant MS 050 curriculum did not assist the students in remediating these deficiencies in mathematics. The students were theorized to be brute force memorizing enough problems to survive MS 050 and then falling apart in MS 098 Transition to Algebra. Brute force memorization failed to cope with the increasing complexity of the mathematics and did not produce a coherent body of knowledge of mathematics in the student’s minds.
Many of our students have had ten and more years of elementary and secondary mathematics under the tutelage of competent instructors. The instructional method favored is textbook based drill and practice. The students have not learned math during ten years of drill and practice, how could another 16 weeks of the same treatment be expected to be effective?
The hope of the MS 050 Conceptual Approach curriculum was to build a knowledge of mathematics on the rules of mathematics rather than on repetitive problem solving. To achieve this a spiral curriculum built around patterns in mathematics and concrete models of mathematics was designed. The students would take a pattern in mathematics or concrete model of mathematics from arithmetic to algebra and then return to arithmetic to take a new pattern or model from arithmetic back up to algebra. Many patterns, such as Pascal’s triangle, repeated in new contexts or appeared in a concrete model.
The thrust would be to teach mathematics as a set of systematic rules and organized rule based patterns. The repeated appearance of patterns in multiple contexts was to attempt to force the students to move from a concrete conception of mathematics into abstract forms of math. For example, the link between the number of subsets of a set and binary probabilities provided by Pascal’s triangle creates the opportunity to hold up four different balls and ask the class, "How many pennies am I holding up?"
Where drill and practice are the equivalent of trying to learn English by memorizing a dictionary, the Conceptual Approach would pursue the grammatical rules of mathematics. Concrete models and activities would provide physical and kinetic mental "hooks" on which the students could hang new knowledge and new understandings.
Unlike most drill and practice approaches, the course did not move in a linear sequence from more basic knowledge in math to more complex knowledge in mathematics. The course also did not include working sets of problems, arithmetic and algebra problems were done only in the context of the model or pattern being examined. Thus the starting point sequence 1+2+3+4+5+6 = 21 led eventually to , yet quadratic equations per se were never studied as a general equation form. Note too that is considered post MS 050 material in the extant curriculum in use at the College. The course was centered in arithmetic but each upward spiral through math ended in algebra. The other odd feature was that higher forms of mathematical notation would appear with only minimal introduction - the students were presumed to have prior knowledge and acquaintance with the features of algebra.
The prediction was that the students who passed MS 050 Conceptual Approach would achieve a higher rate of success in MS 098 Transition to Algebra.
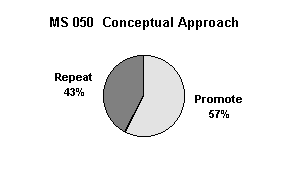
The department did not predict a higher rate of student success in MS 050, the prediction was only that students who attained success in MS 050 Conceptual Approach would outperform their peers in MS 098 who had attained success in the extant MS 050 curriculum. The prediction that success rates in MS 050 would not differ was borne out at the end of the Fall term in 1996. The success rate of students in the Conceptual Approach curriculum and the Extant Curriculum did not differ (p = 0.53 on chi-squared test).
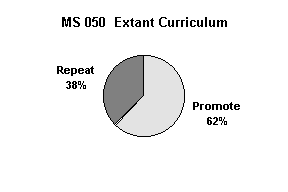
The percentage of students who were promoted out of MS 050 was effectively equal. Any difference in success in the subsequent course, MS 098, ought not be due to differences in the selectivity of the instructors in the MS 050 course in the Fall of 1996. Were one of the approaches to have a smaller promotion rate, one might expect increased success in the subsequent course due to increased selectivity.
The students who passed MS 050 in the Fall of 1996 went into one of five sections of MS 098 taught by one of four different instructors in the Spring of 1997.
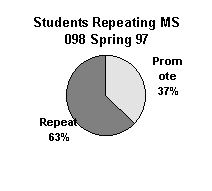
This study examines whether the MS 050 Conceptual Approach was effective preparation for MS 098. A side question that was also looked at was whether students who did not successfully complete MS 098 in the Fall of 1996 succeeded or failed in MS 098 in the Spring of 1997.
The following data was obtained in the Spring of 1997:
| MS 098 Students Spring 97 | Promoted to MS 100 | Will repeat MS 098 |
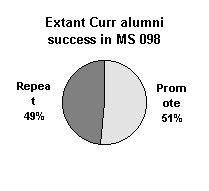
| MS 050 Extant Curriculum alumni | 18 | 17 |
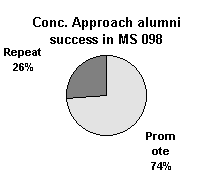
| MS 050 Conceptual Approach alumni | 14 | 5 |
| MS 098 Fall 96 repeating MS 098 in Spring 97 | 19 | 32 |
| Grade MS 098 Spring 97 |
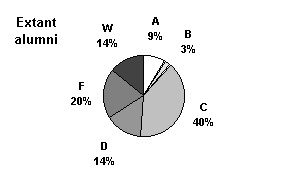
Extant Curriculum/ number students |
Conceptual Approach /number students |
| A | 3 | 1 |
| B | 1 | 4 |
| C | 14 | 9 |
| D | 5 | 1 |
| F | 7 | 0 |
| W | 5 | 4 |
| Sum: | 35 | 19 |
The underlying grade distributions involve sub-statistical numbers and are provided for informational purposes only. Students with a D in mathematics sequence repeat the course.
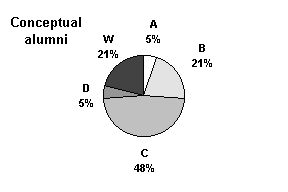
The Conceptual Approach alumni experienced a higher rate of success in MS 098 than the extant curriculum alumni (p = 0.05 on a chi-squared test). Roughly three-quarters of the MS 050 Conceptual Approach alumni successfully completed MS 098.
Students who have failed a course once are at high risk of failing a course on subsequent attempt. Students who repeat a course once are at risk of repeating the course more than two times. A former professor and lover of felines at the College referred to this effect as the "fur ball" effect: multiple repeat students become stuck at a particular course level in mathematics and do not get "coughed up" to the next level.
The MS 050 Conceptual Approach curriculum appears promising. The alumni of this experimental curriculum experienced a statistically significant higher success rate in their next course than their peers who were in sections that used the existing curriculum at the College. This is the first time the department of mathematics has found an approach that increases subsequent success for our Micronesian students.
Although not meaningful statistically, no Conceptual Approach alumni failed MS 098 with a grade of F. Four students withdrew and one obtained a D. Withdrawals, although often due to poor performance, can be due to a number of different factors such as absences, family problems, and other non-academic variables. In the lack of F’s there is the hint that the Conceptual Approach students were even better prepared than their repeat rate indicates.
One concern expressed prior to implementation of the Conceptual Approach was that the curricula might have a negative impact on some students. This concern centered around the potential that some student might have learning styles that would not respond well to the Conceptual Approach.
This negative effect, if it occurred, ought to have shown up in having a large percentage of the MS 050 Conceptual Approach alumni who failed the course in the Fall of 1996 passing MS 050 in the Spring of 1997 under the extant curriculum at the College. Six students who failed MS 050 Conceptual Approach in the Fall of 1996 went on to take MS 050 in the Spring of 1997. Of the six students repeating MS 050 who were in the Conceptual Approach course in the Fall only two students passed in the Spring. This is a rate comparable to the subsequent pass rate seen in repeating students (on the order of one third of the students repeating a course pass on the subsequent attempt). This suggests that the Conceptual Approach probably did not fail anyone who would not have failed under the traditional extant curriculum. That is, the students who failed under the Conceptual Approach would likely have failed under the traditional extant curriculum.
There was a Conceptual Approach alumnus who had failed the course in the Fall of 1996 and who then went on to take MS 098 in the Spring of 1997. The student should have repeated MS 050 in the Spring, but the student did not. This student then failed MS 098 in the Spring of 1997. This suggests that the Conceptual Approach was not beneficial to a student who had failed the course. This sounds self-evident, but the Conceptual Approach benefited only those students who passed the course.
Caution should be exercised prior to throwing celebrations in the street. The Conceptual Approach is an unusual approach in a College classroom. The curriculum demands an instructor with a high level of mathematical knowledge, a strong understanding of Piagetian learning sequences, a thorough knowledge of hands-on approaches to learning, an ability to hold the content at the appropriate level, and an ability to construct curriculum.
The modes of failure of the Conceptual Approach are many. The most common failure mode is that, in the hands of an instructor without the appropriate mathematical maturity, the curriculum devolves into "Let’s have fun playing with stuff." The content disappears and everyone has a good time learning nothing.
Another failure mode known is that the Conceptual Approach is an open approach. The instructor must be able to handle a curriculum that is driven by student mathematical needs rather than by a textbook. The instructor may have to swerve onto new paths to remedy a gap in the student’s knowledge or to chase an idea that has captured the interest of the students. The instructor has to be creative and a builder of their own curricula guided by the student’s needs. This is difficult for an instructor who is accustomed to the predictability of a textbook based course. Teaching the Conceptual Approach is impossible for an instructor who cannot function without a test question bank book. The Conceptual Approach is an outline and a collection of possibilities that must be adapted to each class individually. The instructor who needs a highly structured curriculum cannot handle the Conceptual Approach.
The skill set required of the instructor is not likely to be found in a person with less than a Master’s degree in Mathematics, or at least a Master’s in mathematical or science secondary education. The course content pulls material from many different fields of mathematics and coherently weds this knowledge to the group work oriented world of hands-on science education.
The course also requires physical models of mathematics -- the purchase of materials as would be more typically seen in a physical science type of course. In the present absence of a textbook, the course may be less expensive for the student, but the course is more expensive for the school. These costs are not large, but the needs of the course will vary from term to term. If a particular pattern or model ignites the students, the instructor will be redesigning the daily class plans on the fly to take advantage of the student’s interest. This virtually requires the existence of a small petty cash fund to make small purchases. Typical sorts of Conceptual Approach material would include yarn, golf balls, marbles, possibly even gummy bears. Most Conceptual Approach materials are of the everyday variety.
Whether or not the Conceptual Approach curricula can be utilized more broadly remains to be seen.
The fourteen Conceptual Approach alumni and 18 extant curriculum alumni who passed MS 098 will be followed to see what, if any longer term impacts there might be on these students.
Return to home page
Page comments