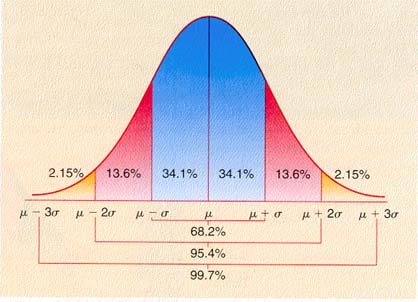
- The highest acceptable body fat for young females is 31. What percent of the
female students have body fat lower than 31? That is, find P(x<31).
- The lower limit of obesity for young females is 39. What percent of the female
students have a body fat higher than 39? That is, find P(x>39).
- If there are 400 female students, how many are obese?
- Suppose the College receives a grant to target the 80 most obese female students (equals
the top 20%) with a diet and exercise program. What body fat should be set as the lower
limit for entry into the program. That is, find P(x > ?) = 0.20.
- Construct a 95% confidence interval for the population mean m
for SCA.
- Does the 95% confidence interval for SCA include the Berea Christian High School sample
mean
 TOEFL score of 481?
TOEFL score of 481?
10.5, 14.7, 16.4, 18.2, 19.8, 23.4, 25.7, 30.2, 32.5, 35.2, 45.9