For a sample size of n = 13 years (1971 to 1983 inclusive) the sample mean number of
suicides in Chuuk state was ![]() = 9.92
suicides per year with a sample standard deviation of sx = 5.09 suicides per year.
Construct a 95% confidence interval for the population mean m
number of suicides per year in Chuuk State.
= 9.92
suicides per year with a sample standard deviation of sx = 5.09 suicides per year.
Construct a 95% confidence interval for the population mean m
number of suicides per year in Chuuk State.
| Statistic or Parameter | Symbol | Equations | Excel |
|---|---|---|---|
| Basic Statistics | |||
| Square root | Ö | =SQRT(number) | |
| Sample size | n | =COUNT(data) | |
| Sample mean | Sx/n | =AVERAGE(data) | |
| Sample standard deviation | sx | =STDEV(data) | |
| Normal Statistics | |||
| Calculate a z value from an x | z | = |
=STANDARDIZE(x, m, s) |
| Calculate an x value from a z | x | = s z + m | = s*z+m |
| Calculate a z value from an |
z | 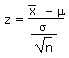 |
|
| Calculate an |
=m + zc*sx/sqrt(n) | ||
| Find a probability p from a z value | =NORMSDIST(z) | ||
| Find a z value from a probability p | =NORMSINV(p) | ||
| Confidence interval statistics | |||
| Degrees of freedom | df | = n-1 | |
| Find a zc value from a confidence level c | zc | =ABS(NORMSINV((1-c)/2)) | |
| Find a tc value from a confidence level c | tc | =TINV(1-c,df) | |
| Calculate an error tolerance E of a mean for n ³ 30 using sx | E | =zc*sx/SQRT(n) | |
| Calculate an error tolerance E of a mean for n < 30 using sx. Can also be used for n ³ 30. | E | =tc*sx/SQRT(n) | |
| Calculate a confidence interval for a population mean m from
a sample mean |
|||
| Hypothesis Testing | |||
| Calculate a t-statistic | t |  |
|
The original data:
| Year | Male | Female | Total |
| 1971 | 4 | 0 | 4 |
| 1972 | 4 | 1 | 5 |
| 1973 | 3 | 0 | 3 |
| 1974 | 8 | 0 | 8 |
| 1975 | 15 | 0 | 15 |
| 1976 | 5 | 0 | 5 |
| 1977 | 10 | 0 | 10 |
| 1978 | 6 | 1 | 7 |
| 1979 | 15 | 2 | 17 |
| 1980 | 16 | 1 | 17 |
| 1981 | 13 | 3 | 16 |
| 1982 | 11 | 1 | 12 |
| 1983 | 9 | 1 | 10 |