1. The male students at the national campus have a mean body fat index m = 20.3 and a standard deviation s = 8.3. Consider the distribution of the data to be normal.
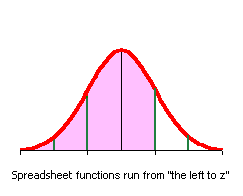
   1. X ® Z ® Prob: Find the probability that a male student at the national campus has a body fat index higher than 25 (obese).
      P( x > 25) = ______________________
      
      
   2. If there are 400 men on the campus, how many are obese?   ______________
      
      
   3. Prob ® Z ® X: Suppose I want to test run a new exercise and diet program that might reduce obesity. I decide to test the program on the most obese 20% of the men on the campus.  What is the minimum body fat index for entry into this new program?
      P( x > ______________) = 0.20
      
      
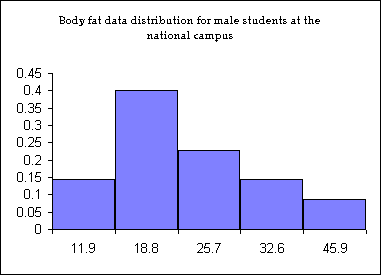
   4. Toughie: the histogram depicts the actual distribution of the body fat data for the men at the national campus. Note that the actual distribution is skewed right. Does this mean your answer to 1a is an overestimate (too large) or an underestimate (too small)?
      

Calculate a z value from an x	z	=	=STANDARDIZE(x, m, s)
Calculate an x value from a z	x	= s z + m	= s*z+m
Find a probability p from a z value			=NORMSDIST(z)
Find a z value from a probability p			=NORMSINV(p)

Lee Ling home COM-FSM home page