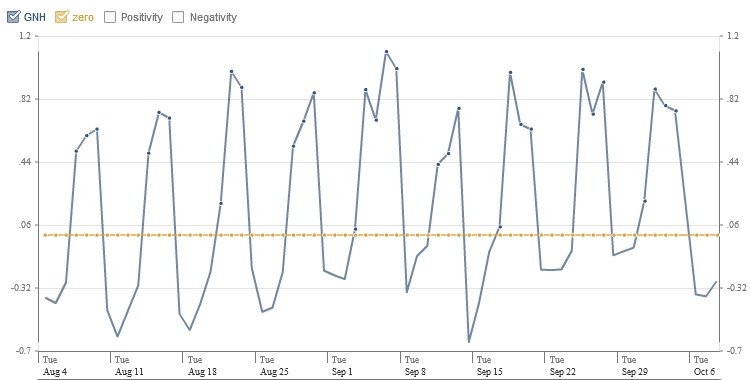

United States Gross National Happiness (GNH) Every day, millions of people share how they feel with the people who matter the most in their lives through status updates on Facebook. These updates are tiny windows into how people are doing. They're brief, to the point and descriptive of what's going on this week, today or right now. Grouped together, these updates are indicative of how we are collectively feeling. Measuring how well-off, happy or satisfied with life the citizens of a nation are is part of the Gross National Happiness movement. When people in their status updates use more positive words--or fewer negative words--then that day as a whole is counted as happier than usual.
The graph represents our measure of Gross National Happiness. There are two components of GNH: The extent to which words used on that day were positive and negative. Gross National Happiness is the difference between the positivity and negativity scores based on the number of positive and negative words used that day. Zero is a neutral day with equal positivity and negativity scores.
For the purposes of this quiz, presume that the Gross National Happiness data is normally distributed with a mean μ of 0.25 and a standard deviation σ of 0.38.
See also: Is It a Day to Be Happy? Check the Index