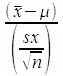
Minutes
2.77
2.58
2.68
2.45
2.47
2.48
2.52
2.52
2.59
2.76
2.56
2.71
2.84
2.65
2.90
2.78
2.78
2.73
2.74
2.42

MS 150 Statistics q09 "Part IV": Hypothesis Testing • Name:

On Wednesday evening 09 April 2008 I decided to go out and get some numbers for the Friday quiz. New numbers are always the best. Back in 2006 my mean joggling lap time was 2.55 minutes. Treat 2.55 as my pre-existing, previously known value. Use 2.55 minutes as my population mean μ lap time.

Wednesday evening I joggled twenty laps, with the times as given in the table. All times in the table are in minutes. The decimal is also in minutes. This is the sample. Could this sample come from a population with a mean μ of 2.55 minutes? That is the essence of this hypothesis test.

Use an alpha of α = 0.05 for the hypothesis test.

Null hypothesis: H0: μ = 2.55 minutes
Alternate hypothesis: H1: μ ≠ 2.55 minutes

  1. n = __________ Find the sample size n for the data.
  2. x = __________ Find the sample mean x.
  3. sx = __________ Find the sample standard deviation sx.
  4. tc = __________ Determine tcritical using an α = 0.05
  5. x = __________ What will be our level of confidence c in our result?
  6. t = __________ Calculate the t-statistic.
  7. __________ Is the difference in the mean lap times statistically signficant?
  8. ________________________________________ Would we reject the null hypothesis or fail to reject the null hypothesis that the sample mean is statistically significantly different from the population mean μ at an α of 5%?
  9. __________ Could the twenty lap sample come from a population with a population mean lap time μ of 2.55 minutes?
  10. __________ Am I statistically significantly slower than two years ago?

Formulas are written for OpenOffice.org Calc. Replace semi-colons with commas for Excel.

Hypothesis testing for a sample mean versus a known population mean
Statistic or ParameterSymbolEquationsOpenOffice
Relationship between confidence level c and alpha α for two-tailed tests 1 − c = α
Calculate t-critical for a two-tailed test tc=TINV(α;df)
Calculate a t-statistic t 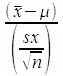t-statistic =(x - μ)/(sx/SQRT(n))
Calculate a two-tailed p-value from a t-statisticp-value = TDIST(ABS(t);df;2)

Statistics • Courses • COMFSM