MS 150 Statistics q08 • Name:

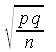
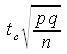
For a sample size n of 100 visitors to Safalra.com, user-agent strings submitted by their browsers showed that 52% of the visitors were using Gecko based browsers such as Mozilla FireFox. Find the 95% confidence interval for the population proportion P for users of Gecko based browsers who visit Safalra.com.

  1. ____________________ Write the sample size n.
  2. ____________________ Write down the sample success proportion p as a decimal.
  3. ____________________ Calculate q.
  4. ____________________ Calculate the standard error of the proportion.
  5. ____________________ Find the degrees of freedom.
  6. ____________________ Calculate t-critical tc for a confidence level c of 0.95.
  7. ____________________ Calculate the margin of error E for the proportion.
  8. Write out the 95% confidence interval for the population proportion:

    p(___________ ≤ P ≤ ___________) = 0.95
  9. ____________________ Visitors using the Microsoft Internet Explorer were 40% of the sample. Is the Gecko based browser usage in the population statistically significantly greater than the Microsoft Internet Explorer usage?

Formulas are written for OpenOffice.org Calc. Replace semi-colons with commas for Excel.

Confidence interval statistics for proportions
Statistic or ParameterSymbolEquationsOpenOffice
Number of successes or desired results in a sampler
Proportion of successes or desired result in a samplep r ÷ n=r/n
Proportion of non-successes, not the desired, or alternate result in a sample q1 − p=1-p
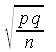
Standard error of a proportion p σp standard error of a proportion =SQRT(p*q/n)
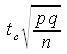
Margin of error E for a proportion p E Margin of error E for a proportion p =TINV(1-c;n-1)*SQRT(p*q/n)
Calculate a confidence interval for a population proportion P from the sample proportion p and the margin of error E for the mean. p − E ≤ P ≤ p + E