MS 150 Statistics prequiz spring 2008 • Name:
Data
| Jumps |
|---|
| 8 |
| 17 |
| 20 |
| 22 |
| 34 |
| 42 |
| 45 |
| 58 |
| 107 |
| 213 |
Part I: Basic Statistics
On Thursday 08 November 2007 a jump rope contest was held at a local elementary school festival. Data for this prequiz derives from this contest. Contestants jumped with their feet together, a double-foot jump. The data seen in the table on the right is the number of jumps for ten female jumpers. Note that while the number of jumps data is discrete, treat the data as if it were continuous data. For the data in the table...
- _________ Determine the sample size n.
- _________ Determine the minimum.
- _________ Determine the maximum.
- _________ Calculate the range.
- _________ Calculate the midrange.
- _________ Determine the mode.
- _________ Determine the median.
- _________ Calculate the sample mean x.
- _________ Calculate the sample standard deviation sx.
- _________ Calculate the sample coefficient of variation.
Part II: Linear Regression (best fit or least squares line)
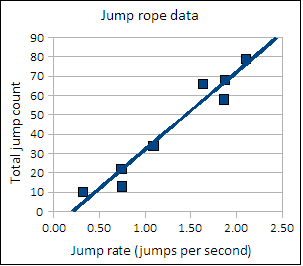
The data in this section continues the exploration of jump rate versus the jump count. The jump rate in jumps per second is the independent variable x. The total number of jumps (jump count) is being treated as the dependent variable y.
Jump rate versus count
| Rate | Count |
|---|
| 0.32 | 10 |
| 0.74 | 22 |
| 0.75 | 13 |
| 1.09 | 34 |
| 1.63 | 66 |
| 1.86 | 58 |
| 1.87 | 68 |
| 2.10 | 79 |
- _________ Calculate the slope of the linear regression (best fit line).
- _________ Calculate the y-intercept of the linear regression (best fit line).
- _________ Is the relation between jump rate and jump count positive, negative, or neutral?
- _________ Calculate the linear correlation coefficient r for the data.
- ______________ Is the correlation none, weak/low, moderate, strong/high, or perfect?
- ______________ Determine the coefficient of determination.
- ______________ What percent in the variation in jump rate "explains" the variation in the jump count?
- _________ Use the slope and intercept to predict the number of jumps for a jumper with a jump rate of 1.00
- _________ Use the slope and intercept to determine the rate necessary to obtain 213 jumps.