MS 150 Statistics quiz 04 fall 2007 • Name:
INS marasong
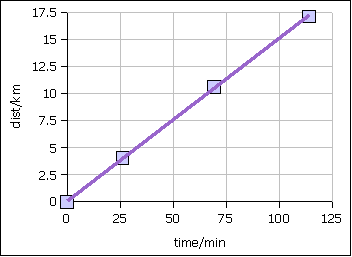
| time/min (x) | dist/km (y) |
|---|
| 0 | 0.0 |
| 26 | 4.0 |
| 69 | 10.6 |
| 114 | 17.06 |
Linear regression: On the 21st
of July I completed the INS "marasong" half marathon. As I ran I tracked my time in minutes (min) and distance in kilometers (km) using a GPS. The data is given in the table above.
- ______________ Does the relationship between time and distance appear to be linear, non-linear, or random?
- ______________ Determine the slope of the linear regression (best fit line) for the data.
- ______________ Determine the y-intercept of the linear regression for the data.
- ______________ Determine the correlation coefficient r.
- ______________ Is the correlation positive or negative?
- ______________ Is the correlation none, weak, moderate, strong, or perfect?
- ______________ Determine the coefficient of determination.
- ______________ What percent in the variation in time "explains" the variation in distance?
- ______________ What would be the predicted distance after 45 minutes of running?
- ______________ What would be the predicted time for me to reach the finish line at Spanish wall at 20.3 kilometers?
- ______________ What is the probability of rolling a six on a twelve sided die numbered from one to twelve?
- ______________ What is the probability of rolling a three or a multiple of three on a fifteen sided die numbered one to fifteen?
- ________________________ Can a die be one-sided? What shape would a one-sided die be?
- What are the three ways of determining a probability?

