MS 150 Statistics Test 3 • Name:
The table below uses the number of heads on tosses of nine pennies as the bin values x. The frequency is the number of tosses out of 1305 which came up for the number of heads shown.
Number of heads on tosses of nine pennies
| Heads (x) | Freq f | Rel Freq p(x) | x * p(x) |
|---|
| 0 | 1 | | |
| 1 | 14 | | |
| 2 | 43 | | |
| 3 | 118 | | |
| 4 | 178 | | |
| 5 | 198 | | |
| 6 | 121 | | |
| 7 | 50 | | |
| 8 | 6 | | |
| 9 | 0 | | |
| | 729 | | |
- _____________ Determine the population mean number of heads per toss u.
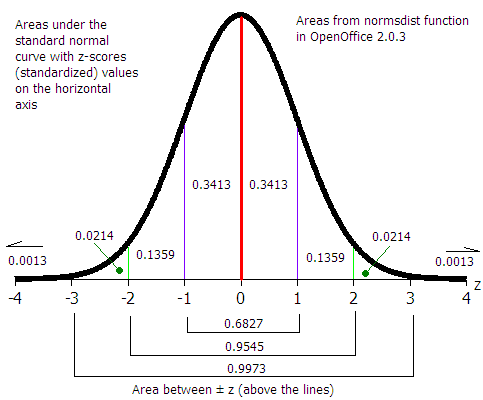
In training for the upcoming half marathon on the 21st July I am averaging μ = 9.1 kilometers per hour with a standard deviation σ = 0.6 kilometers per hour. Use these numbers in the following calculations.
- ______________ If my speed falls below 8.4 kilometers per hour, then the duration of my run will exceed my endurance limit. In other words, at speeds less than 8.4 kilometers per hour I will be moving so slowly that I will exceed the two and half hours I am able to run. Presume that my speeds are normally distributed and use the normal distribution to determine the probability that my speed will be less than 8.4 kilometers per hour.
- ______________ If my speed is faster than 10 kilometers per hour I am likely to win prize money. Calculate the probability that my speed will exceed 10 kilometers per hour.
- ______________ What is the speed below which are the 20% slowest speeds? This number is useful as it tells me when I performing significantly below par. Nota bene: This is an area p to x problem!
- ______________ When I am training I track my speed in real time using a GPS unit. To optimize my training my speed should remain in the upper 33% of my speed range. Calculate the speed above which (faster than) is 33% of the area under the normal curve. This speed is the minimum speed I should strive to hold while training.
Table of statistical functions used by OpenOffice
| Statistic or Parameter |
Symbol |
Equations |
OpenOffice.org Calc |
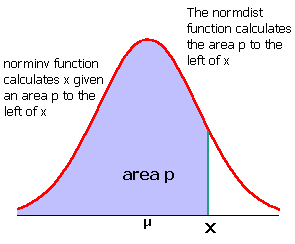
| Find a probability p (the area to the left of x) from an x value |
|
|
=NORMDIST(x;μ;σ;1) |
| Find an x value from a probability p (the area to the left of p) |
|
|
=NORMINV(p;μ;σ) |