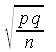
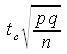
| Building | Cost $/feet² |
|---|---|
| Classroom A | 0.26 |
| Classroom B | 0.16 |
| Cafeteria C | 0.39 |
| Dormitory D | 0.19 |
| Dormitory E | 0.18 |
| Faculty F | 0.80 |
| Faculty F2 | 0.67 |
| Administration G | 0.53 |
| Library H | 0.52 |
| Bookstore K | 0.57 |
| Agriculture L | 0.55 |
The table provides the power cost per square foot for the buildings on the Palikir campus. Construct a 95% confidence interval for the population mean cost in dollars per square foot (feet²).
You will be given a penny. Using a sample size of ten flips, you will be investigating whether a population probability of 0.50 for heads is a possibility. Flip the penny ten times. Record the number of heads r. Use the number of heads/ten flips as your sample proportion p for the proportion of heads (p = r/n). Find the 95% confidence interval for the population proportion P. Use a spreadsheet to make your calculations, rounding answers to two decimal places on this test.
Formulas are written for OpenOffice.org Calc. Replace semi-colons with commas for Excel.
| Confidence interval statistics | |||
|---|---|---|---|
| Statistic or Parameter | Symbol | Equations | OpenOffice |
| Degrees of freedom | df | = n − 1 | =COUNT(data)-1 |
| Find a t-critical tc value from a confidence level c and sample size n | tc | =TINV(1-c;n-1) | |
| Standard error of the sample mean | σx |
|
=sx/SQRT(n) |
| Calculate the margin of error E for a mean for n ≥ 5 using sx. | E | =tc*sx/SQRT(n) | |
| Calculate a confidence interval for a population mean μ from the sample mean x and margin of error E for the mean. | x − E ≤ μ ≤ x + E | ||
| Number of successes or desired results in a sample | r | ||
| Proportion of successes or desired result in a sample | p | r ÷ n | =r/n |
| Proportion of non-successes, not the desired, or alternate result in a sample | q | 1 − p | =1-p |
| Standard error of a proportion p | σp |
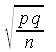
|
=SQRT(p*q/n) |
| Margin of error E for a proportion p | E |
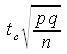
|
=TINV(1-c;n-1)*SQRT(p*q/n) |
| Calculate a confidence interval for a population proportion P from the sample proportion p and the margin of error E for the mean. | p − E ≤ P ≤ p + E | ||