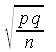
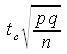

This quiz is less structured than the usual statistics quiz. Work carefully.
Madolehnihmw high school is a fairly new high school on Pohnpei. Last year their first graduating class scored a 24.42 average on the admissions entrance essay test. This year 87 students scored an average 26.86 on the essay section with a standard deviation of 10.23.
Run a hypothesis test at an alpha α at 0.05 to determine if the school has done better using 24.42 as the population mean μ.
Write out the null hypothesis and alternate hypothesis. Determine if the difference is statistically significant. Do you fail to reject the null hypothesis or do you reject the null hypothesis?
Include in your report the p-value and the maximum confidence level we can have that the difference is significant.
This spring 98 of 352 seniors at PICS who took the admissions entrance test gained admission to an associate's degree program. Last year, in spring 2006, 36% of the PICS seniors who took the admissions entrance test gained admission to an associate's degree program. Using last year's 36% percent as the population proportion P, determine if the percent of PICS students gaining admission to an associate's degree program changed from 2006 to 2007 by a statistically significant amount at an alpha α of 0.05.
Write out the null hypothesis and alternate hypothesis. Determine if the difference is statistically significant. Do you fail to reject the null hypothesis or do you reject the null hypothesis?
Include in your report the p-value and the maximum confidence level we can have that the difference is significant.
Formulas are written for OpenOffice.org Calc. Replace semi-colons with commas for Excel.
| Statistic or Parameter | Symbol | Equations | OpenOffice |
|---|---|---|---|
| Confidence interval statistics | |||
| Degrees of freedom | df | = n − 1 | =COUNT(data)-1 |
| Find a t-critical tc value from a confidence level c and sample size n | tc | =TINV(1-c;n-1) | |
| Standard error of the sample mean | σx |
|
=sx/SQRT(n) |
| Calculate the margin of error E for a mean for n ≥ 5 using sx. | E | =tc*sx/SQRT(n) | |
| Calculate a confidence interval for a population mean μ from the sample mean x and margin of error E for the mean. | x − E ≤ μ ≤ x + E | ||
| Number of successes or desired results in a sample | r | ||
| Proportion of successes or desired result in a sample | p | r ÷ n | =r/n |
| Proportion of non-successes, not the desired, or alternate result in a sample | q | 1 − p | =1-p |
| Standard error of a proportion p | σp |
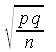
|
=SQRT(p*q/n) |
| Margin of error E for a proportion p | E |
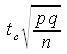
|
=TINV(1-c;n-1)*SQRT(p*q/n) |
| Calculate a confidence interval for a population proportion P from the sample proportion p and the margin of error E for the mean. | p − E ≤ P ≤ p + E | ||
| Hypothesis Testing | |||
| Relationship between confidence level c and alpha α for two-tailed tests | 1 − c = α | ||
| Calculate a t-statistic (t) for a sample mean and population mean | t |  |
=(x − μ)/(sx/SQRT(n)) |
| Calculate t-critical for a two-tailed test for a risk of a type I error alpha α | tc | =TINV(α,df) | |
| Calculate t-critical for a one-tailed test | tc | =TINV(2*α,df) | |
| p-value, two-tailed for the mean | =TDIST(ABS(t),n−1,number_tails) | ||
| maximum possible confidence | 1 − two tail p-value | ||
| Calculate a t-statistic for a sample proportion p and a population proportion P | t | =(p−P)/sqrt(p*q/n) | |