Quiz 10 Hypothesis test using confidence interval • Name:
A road
| x: cars/5 min |
|---|
| 19 |
| 21 |
| 17 |
| 27 |
| 16 |
The data is the number of cars per five minute period passing past some place along some road somewhere on Pohnpei.
Use the sample mean x and the sample standard deviation sx the data given in the table to calculate a 95% confidence interval for the population mean µ number of cars per five minute periods using the student's t-distribution.
- sample size: n = 5 (not the sum of the cars but the number of five minute samples!)
- x = ______________
Calculate the sample mean x number of cars per five minute period.
- sx = ______________ Calculate the sample standard deviation sx number of cars per five minute period.
- confidence level: c = ______________
- degrees of freedom: = ______________
- t-critical: tc = ______________
- Error tolerance E: = ______________
- Calculate the 95% confidence interval for the population mean µ number of cars per five minute period:
P( ___________ ≤ µ ≤ ___________ ) = 0.95
- _________ The overall population mean µ for Pohnpei is 13.89 cars per five minute period. Is the population mean µ of 13.89 "inside" or "outside" the 95% confidence interval?
- _________ The overall population mean µ for Pohnpei is 13.89 cars per five minute period. Test the hypothesis that the road data in the table is statistically significantly different at a confidence level c of 95%. Is the road data given statistically significantly different from 13.89 at 95%?
- _________ Could the data above have come from a population with a mean of 13.89 at a 95% level of confidence?
- _________ Is the road statistically significantly busier (carrying more traffic on average) than the Pohnpei mean of 13.89 at a 95% level of confidence?
- Rerun your hypothesis test at a confidence level c of 0.99, that is, generate a 99% confidence interval.
P( ___________ ≤ µ ≤ ___________ ) = 0.99
- _________ Could the data above have come from a population with a mean of 13.89 at a 99% level of confidence?
- _________ Is the road statistically significantly busier (carrying more traffic on average) than the Pohnpei mean of 13.89 at a 99% level of confidence?
| Statistic or Parameter | Symbol | Equations | Excel |
|---|
| Confidence interval statistics |
|---|
| Degrees of freedom |
df |
= n-1 |
=COUNT(data)-1 |
| Find a tc value from a confidence level c and sample size n |
tc |
|
=TINV(1-c;n-1) |
| Calculate an error tolerance E of a mean for any n ≥ 5 using sx. |
E |
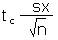 |
=tc*sx/SQRT(n) |
| Calculate a confidence interval for a population mean µ from
the sample mean x and error tolerance E: |
|
x-E ≤ µ ≤ x+E |
|