Quiz 09 | 9 - 10 • Name:
The following problem is based on the garment (clothing) exports from the FSM. All numbers quoted are in 1000s of dollars in order to simplify the arithmetic. During a sample size n = 12 months of 2002 the sample mean was x = 308 (1000's of dollars) with a standard deviation of sx = 108. Calculate a 95% confidence interval for the expected range of the population mean µ based on the 12 month sample data using the student's t-distribution.
- sample size: n = ______________
- sample mean x = ______________
- sample standard deviation sx = ______________
- confidence level: c = ______________
- degrees of freedom: = ______________
- t-critical: tc = ______________
- Error tolerance E: = ______________
- Calculate the confidence interval for the population mean arrival time:
P( ___________ ≤ µ ≤ ___________ ) = 0.95
- _________ The FSM has a population mean µ export value for garments of 248 (1000's of dollars) per month for six years between 1992 and 2002. Use 248 as the population mean µ. Does the 2002 sample mean monthly garment exports represent a statistically significant difference from the population mean µ at a 95% level of confidence?
- _________ Did the FSM generate a statistically significant higher mean monthly income in 2002 from garments at a 95% level of confidence?
Run another set of confidence interval calculations, this time calculating a 90% confidence level for the same monthly sample data.
- confidence level: c = ______________
- t-critical: tc = ______________
- Error tolerance E: = ______________
- Calculate the confidence interval for the population mean arrival time:
P( ___________ ≤ µ ≤ ___________ ) = 0.90
- _________ The FSM has a population mean µ export value for garments of 248 (1000's of dollars) per month for six years between 1992 and 2002. Use 248 as the population mean µ. Does the 2002 sample mean monthly exports represent a statistically significant difference from the population mean µ at a 90% level of confidence?
- _________ Did the FSM generate a statistically significant higher mean monthly income in 2002 from garments at a 90% level of confidence?
- Tough and arguably tricky: Which analysis is correct and WHY?
| Statistic or Parameter |
Symbol |
Equations |
Excel |
|---|
| Calculate a t-statistic t |
t |
 |
=(x - µ)/(sx/SQRT(n)) |
| Find a tc value from a confidence level c and sample size n |
tc |
|
=TINV(1-c,n-1) |
| Calculate an error tolerance E of a mean for any n ≥ 5 using sx. |
E |
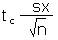 |
=tc*sx/SQRT(n) |
| Calculate a confidence interval for a population mean µ from
a sample mean x and an error tolerance E |
|
x-E≤ µ
≤x+E |
|

