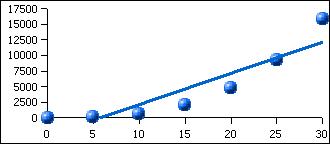
Wind speed (mph)	Power (Watts)
0	0
5	75
10	588
15	1980
20	4700
25	9190
30	15876
1	499.79	Calculate the slope of the linear regression (trend line) for the data.
2	-2866.93	Calculate the y-intercept of the linear regression (trend line) for the data.
3	positive	Is the correlation positive or negative?
4	17124.5	Calculate the projected power production in Watts for a wind speed of 40 mph.
5	7.74	Calculate the wind speed for which power production is 1000 Watts.
6	0.9064	Determine the correlation coefficient r.
7	high or strong	Is the correlation none, low, moderate, high, or perfect?
8	non-linear	Does the relationship appear to be linear or non-linear?
9	0.8216	Determine the coefficient of determination.
10	82.16%	What percent in the var in wind speed accounts for the var in the kilowatt hours?
11	Yes	In this case, is there causation?
	[ans will vary]	Why or why not?