WrtiMS 150 Statistics Quiz 10 Name: ______________________________
Hypothesis testing for binomial probabilities
A couple of years ago a staffer at the Marshall Islands department of education noted in a newspaper article that Marshall's Island public school system was not the weakest in Micronesia. The staffer noted that Marshall's was second weakest, commenting that education metrics in the Marshall's outperform those in Chuuk's public schools.
Today's quiz takes you through the hypothesis test from the point of view of admissions to COM-FSM. This is by NO means any form of definitive proof of anything, just a potential indicator of whether the MIDOE staffer is possible on the mark or clueless.
In 2004 fifty students at Marshall Islands High School took the entrance test. 10 Achieved admission to regular and IEI programs. In the same year CHS had 257 students taking the test, of which 17 gained admission. Note that the 240 number in the homework was an error, I misread a table. 240 was the number who gained certificate admission.
The null hypothesis would be one of no difference in the probabilities: H0: pdiff = 0
The alternate hypothesis would be: H1: pdiff ≠ 0
Run the test at an alpha of 0.01 just to be sure to minimize the risk of a type I error.
|
n1 = 257 r1 = 17 p1 = 0.07 q1 = 0.93 |
n2 = 50 r2 = 10 p2 = 0.20 q2 = 0.80 |
|
|
School |
n |
r |
p |
q |
|
1 |
CHS |
257 |
17 |
0.07 |
0.93 |
|
2 |
MIHS |
50 |
10 |
0.20 |
0.80 |
1. Determine![]() using
:
using
:![]()
2. Determine using
![]() :
:
3. Determine tc using tinv(0.01,49):
4. Find t using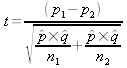 :
:
5. Will you reject the null hypothesis or will you fail to reject the null hypothesis? _____
6. Is the difference in the percentages statistically significant? ___________
7. Does this test lend support to the staffer's position? ______________
8. The point after: Calculate the maximum possible level of confidence at which the null hypothesis could be rejected: