MS 150 Spring 2004 Test Two Name:
The mathematics division is a study of performance in mathematics courses at the national campus for spring 2003 and fall 2003 as measured by grade point averages (GPA) by gender and state. The following table shows the mean GPA at the national campus for each the eight gender/state subgroups and their standard deviations. We will consider these as population values as all grades from spring 2003 and fall 2003 were included in the study. For the purposes of this test, presume the data is normally distributed.
Spring 2003 and fall 2004 math GPA data
| Gender State | sample size n
(number of students) | mean GPA µ | stdev GPA s |
|---|
| Female Chuuk | 83 | 1.41 | 1.22 |
|---|
| Female Kosrae | 29 | 2.14 | 1.27 |
|---|
| Female Pohnpei | 296 | 1.85 | 1.35 |
|---|
| Female Yap | 47 | 2.15 | 1.50 |
|---|
| Male Chuuk | 81 | 1.60 | 1.37 |
|---|
| Male Kosrae | 40 | 2.00 | 1.24 |
|---|
| Male Pohnpei | 239 | 1.87 | 1.33 |
|---|
| Male Yap | 69 | 1.96 | 1.33 |
|---|
The following is a set of normal curves for the above eight subgroups:
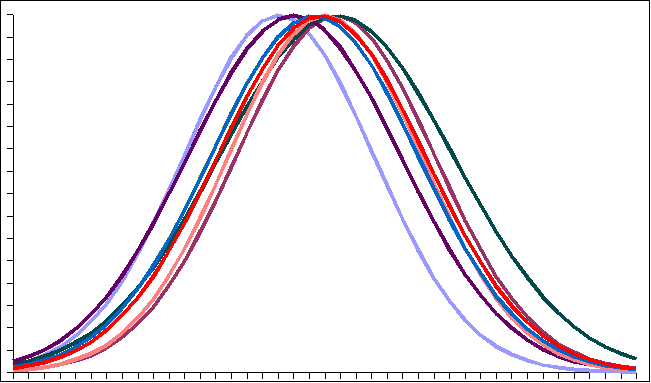
- ______________ Which of the eight subgroups is represented by the normal curve the farthest to the right? Use the values in the table to help you determine which curve is farthest to the right.
- ______________ Which of the eight subgroups is represented by the narrowest (and hence tallest) normal curve? Note that differences are small, so you will have to examine the values in the table to determine which is the narrowest.
- n = __________ What is the sample size n for the Chuukese females?
- µ = __________ What is the mean GPA µ for the Chuukese females?
- s = __________ What is the standard deviation s for the Chuukese females?
- z = __________ Convert x = 2.00 to a z value for the Chuukese females.
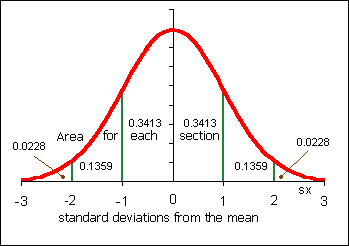
- p(x > 2.00) = __________ Find the probability (the area under the normal curve) that a Chuukese female has a GPA ABOVE 2.00.
- x = __________ The data for all eight subgroups represents 884 students with mean GPA µ of 1.83 and a standard deviation s of 1.33. Suppose I want to find the GPA cut-off for the top 15% of the students and use that to establish an "honors" GPA. Any student getting above that GPA in their math courses would be a math honors student. What is the GPA value for the top 15% of the students using the mean µ of 1.83 and a standard deviation s of 1.33? Hint: this is an "area to z to x" problem!
| Statistic or Parameter |
Symbol |
Equations |
Excel |
| Calculate a z value from an x |
z |
= 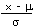 |
=STANDARDIZE(x, µ, s) |
| Calculate an x value from a z |
x |
= s z + µ |
= s*z+µ |
| Find a probability p from a z value |
|
|
=NORMSDIST(z) |
| Find a z value from a probability p |
|
|
=NORMSINV(p) |