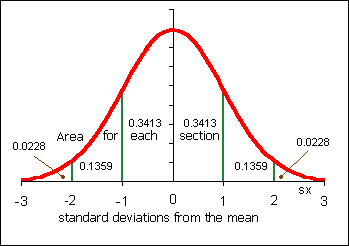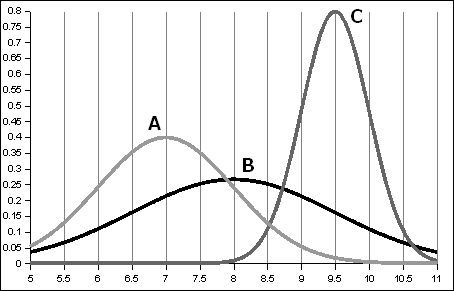
- _______ Which curve has the largest mean?
- _______ Which curve has the largest standard deviation?
- _______ What is the mean for curve A?
- _______ What is the mean for curve B?
- _______ What is the mean for curve C?
- _______ Estimate the standard deviation for curve A
- _______ Estimate the standard deviation for curve B
- _______ Estimate the standard deviation for curve C