MS 150 Statistics Fall 2003 Quiz 6 • Name:
The College of Micronesia-FSM Spring 2003 entrance test had a TOEFL reading mean score of 445 with a standard deviation of s = 65 for 1358 students who took the entrance test. The reading scores were normally distributed.
- n = __________ What is the sample size n?
- µ = __________ What is the mean µ?
- s = __________ What is the standard deviation s?
- z = __________ Use the formula z =
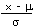 to convert x = 380 to a z value.
to convert x = 380 to a z value.
- z = __________ Use the formula z =
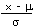 to convert x= 445 to a z value.
to convert x= 445 to a z value.
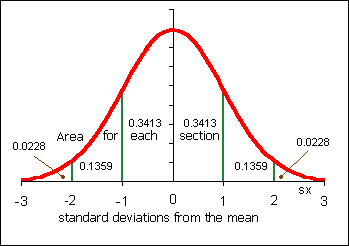
- __________ Suppose the College admitted all students with a reading score above 380 into degree programs in 2003. Further suppose that in 2004 the College decides to only admit students with a reading score above 445. What percent of the students are between 380 and 445?
- __________ Use the percentage calculated in the previous question and the sample size above to determine how many students are between 380 and 445. This is the number of students nationwide who would be affected by change.
- x = __________ Use the formula x = z*s + µ to calculate the reading TOEFL score for students who are z =1 standard deviation above the mean.
- z = __________ The College actually admitted all students above 400 into the IEP program. Use the formula z =
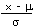 to convert x = 400 to a z value.
to convert x = 400 to a z value.
- z = __________ One proposal would raise the minimum score to 450. Use the formula z =
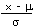 to convert x = 450 to a z value.
to convert x = 450 to a z value.
- ________ Do we know how to determine the area under the normal curve between 400 and 450?