| Statistic or Parameter |
Symbol |
Equations |
Excel |
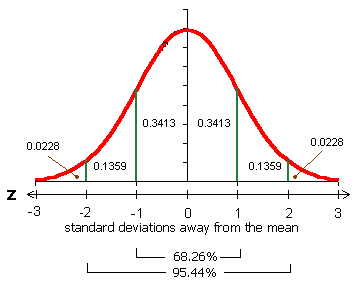
| Normal Statistics |
| Calculate a z value from an x |
z |
= 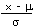 |
=STANDARDIZE(x, µ, s) |
| Calculate an x value from a z |
x |
= s z + µ |
=s*z+µ |
| Calculate a z-statistic from an x |
z |
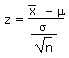 |
=(x - µ)/(sx/SQRT(n)) |
| Calculate a t-statistic (t-stat) |
t |
 |
=(x - µ)/(sx/SQRT(n)) |
| Calculate an x from a z |
|
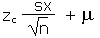 |
=µ + zc*sx/sqrt(n) |
| Find a probability p from a z value |
|
|
=NORMSDIST(z) |
| Find a z value from a probability p |
|
|
=NORMSINV(p) |
| Confidence interval statistics |
| Degrees of freedom |
df |
= n-1 |
=COUNT(data)-1 |
| Find a zc value from a confidence level c |
zc |
|
=ABS(NORMSINV((1-c)/2)) |
| Find a tc value from a confidence level c |
tc |
|
=TINV(1-c,df) |
| Calculate an error tolerance E of a mean for n >= 30 using
sx |
E |
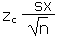 |
=zc*sx/SQRT(n) |
| Calculate an error tolerance E of a mean for n < 30 using sx. Can also be used for n >= 30. |
E |
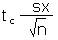 |
=tc*sx/SQRT(n) |
| Calculate a confidence interval for a population mean µ from
a sample mean x and an error tolerance E |
|
x-E<= µ
<=x+E |
|