MS 150 Statistics Quiz 09 9.1 • Name: _______________
Suppose we want to do a study of whether the male students at the national campus experience a change in body fat with age during their years at COM-FSM. Suppose we already know that the population mean body fat percentage for males 18 and 19 years old is µ = 15.96
- ____________________ What is the null hypothesis H0?
- ____________________ What is the alternate hypothesis H1?
- Construct a 95% confidence interval for a sample of n = 27 students aged 21 to 22 years old who have a sample mean body fat
x = 21.68 and a sample standard deviation of sx = 8.05
- Make a sketch of the data
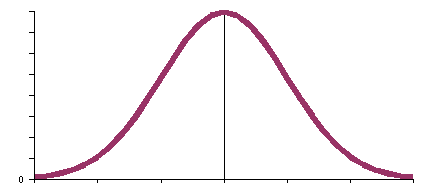
- _______ Find c for a 95% confidence interval.
- _______ Find the degrees of freedom (df).
- _______ Calculate t-critical (tc) using =TINV(1-c,n-1)
- _______ Calculate the Error E using E =
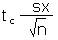
- Use the Error E calculated above to calculate the 95% confidence interval from x - E < µ < x + E:
_________ < µ < _________
- The confidence interval for the population mean µ is:
P( _________ < µ < _________ ) = _________
- _________ Is the 18 and 19 year old population mean of µ = 15.96 included in the confidence interval for the sample mean of 21 to 22 year old students?
- _________ Is the change in body fat for the male students statistically significant?
- __________________ Do we reject the null hypothesis H0 of no change or fail to reject the null hypothesis?
- We can determine the largest confidence level c that just reaches the 15.96 value by calculating a t-statistic from the population value, determining the area in the tails beyond the t-statistic, and then calculating the corresponding c. Use sample and population data above to calculate the t-statistic (t):
 = _______________
= _______________
- Calculate the two-tail area beyond the t-statistic (t) using:
=TDIST(ABS(t-statistic),degrees of freedom,2)
= _______________ (this is also called the p value)
- ___________ Calculate (1 - p value) to determine the largest confidence level c we have in this change.

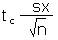
 = _______________
= _______________