| Time in minutes | Number of people | Rel. Freq. P ( x ) | x * P ( x ) |
|---|---|---|---|
| 15 | 63 | ||
| 30 | 28 | ||
| 45 | 35 | ||
| 60 | 30 | ||
| 75 | 37 | ||
| Sums: |
- Calculate the relative frequency P(x) values for the third column.
- Use the fourth column, x*P(x), to calculate the mean length of time for people to commute to the Chuuk campus.
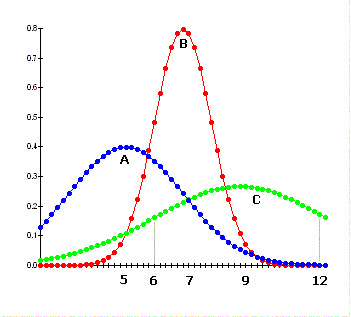
The diagram above depicts three normal curves
- _______ Which curve has the largest mean?
- _______ Which curve has the largest standard deviation?
- _______ What is the mean for curve A?
- _______ What is the mean for curve B?
- _______ What is the mean for curve C?
- _______ What is the standard deviation for curve C?
- What is the probability a batch of Sapporo Draft beer will have an alcohol content of less than 5?
- What is the probability a batch of Sapporo Draft beer will have an alcohol content of between 5.5 and 6.2?
- Suppose, as part of a quality control program, Sapporo plans to not sell the 10% of the batches with the lowest alcohol content. What alcohol content is the value below which a batch will not be sold? Nota bene (hint): This is an inverse problem. The area is the 10% in the left tail.