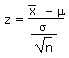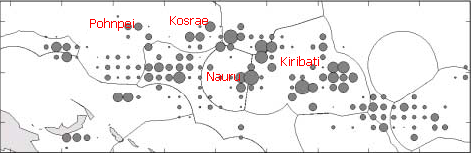
A similar pattern is seen in the high cash-value catches of tuna by FSM owned long liners for export as sashimi:
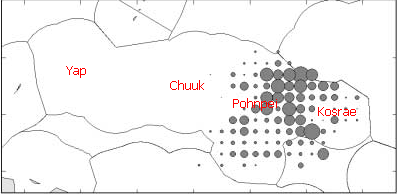
Here the FSM is at the center of the diagram.
Similar patterns of tuna catches are seen for boats from Japan, China, and Taiwan. Over the past five years some states, notably Kosrae and Yap, and some portions of existing states, notably Faichuuk, have engaged in internal discussions about the possibility of declaring themselves independent nations. More recently the individual states have pushed for changes to the constitution that would ensure that money earned from tuna would go to the state in which the tuna was caught (this presumes that the state could somehow "own" its portion of the national Exteneded Economic Zone). Whether pursuing independence or seeking constitutional change, a key factor in obtaining income would be whether tuna is actually caught in that state. Based on the actual patterns of tuna catches, which states would get money from tuna and which states would not?
States that would get the tuna money:
States that would not get tuna money: