Box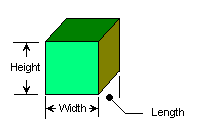
- Measure the Length, width, and height of the box to an accuracy of one millimeter.
Length L: ________ Width w: ________ Height h: ________ - Calculate the volume of the box by multiplying the Length × Width × Height.
Volume ___________________ (be sure to include the correct units!) - Record your Volume on the white board in the box column at the front of the room.
- When every group has recorded their box volume, note the largest and the smallest volume shown on the board.
Largest volume ________________ Smallest volume ________________ - Calculate the average volume of the box by adding all of the volumes on the board and then dividing by the number of measurements of volume made:
Average = Sum of the volumes/Number of measurements = _______________ - Make the following calculations:
Upper half range = Largest volume - Average volume = _____________
Lower Half range = Average volume - Smallest volume ______________ - Fill in the blanks to record the experimentally determined Volume of the box:
____________ ____________ ______________
Average volume + Upper half range - Lower Half Range
Cylinder
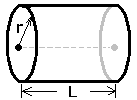
- Measure the radius, and Length of the cylinderox to an accuracy of one millimeter.
radius r: ______________ Length L: _____________ - Calculate the volume of the cylinder by multiplying the πr²L.
Volume ___________________ (be sure to include the correct units!) - Record your Volume on the white board in the cylinder column at the front of the room.
- When every group has recorded their cylinder volume, note the largest and the smallest volume shown on the board.
Largest volume ________________ Smallest volume ________________ - Calculate the average cylinder volume by adding all of the volumes on the board and then dividing by the number of measurements of volume made:
Average cylinder volume = Sum of the volumes/Number of measurements = _______________ - Make the following calculations:
Upper half range = Largest volume - Average volume = _____________
Lower Half range = Average volume - Smallest volume ______________ - Fill in the blanks to record the experimentally determined Volume of the cylinder:
____________ ____________ ______________
Average volume + Upper half range - Lower Half Range
Sphere
- Measure the radius of the sphere to an accuracy of one millimeter.
radius r = _________________
- Calculate the volume of the sphere using the formula for the volume of a sphere:
Volume sphere = ( 4 π r³)/3
Volume ___________________ (be sure to include the correct units!)
- Record the Volume on the white board in the sphere column at the front of the room.
- When every group has recorded their sphere volume, note the largest and the smallest volume shown on the board.
Largest volume _____________ Smallest volume ______________
- Calculate the average sphere volume by adding all of the volumes on the board and then dividing by the number of measurements of volume made:
Average sphere volume = Sum of the volumes/Number of volume measurements = _______________
- Make the following calculations:
Upper half range = Largest volume - Average volume = _____________
Lower Half range = Average volume - Smallest volume ______________
- Fill in the blanks to record the experimentally determined Volume of the sphere:
____________ ____________ ______________
Average volume + Upper half range - Lower Half Range
radius r = _________________
Volume sphere = ( 4 π r³)/3
Volume ___________________ (be sure to include the correct units!)
Largest volume _____________ Smallest volume ______________
Average sphere volume = Sum of the volumes/Number of volume measurements = _______________
Upper half range = Largest volume - Average volume = _____________
Lower Half range = Average volume - Smallest volume ______________
____________ ____________ ______________
Average volume + Upper half range - Lower Half Range