There is a mathematical notation for juggling that describes the possible juggling patterns for a given number of balls. The notation is called site swap notation, alternatively written as a single word siteswap. The numbers are an abstract short hand. The numbers do not tell you how to juggle, the numbers do not tell you where to move your hands, nor whether to throw balls over or under other balls.
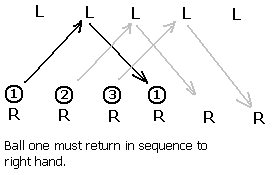
A simple three ball cascade juggle has each of the three balls passing through each of the hands in alternation. Each hand must touch each ball in succession, with the balls being passed from the right to the left and back to the right. The first ball thrown must "fill" the right hand after the third ball has left the right hand.

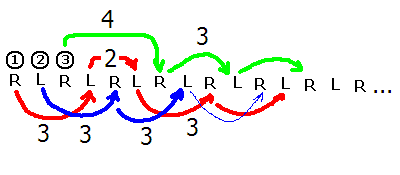
In the above space-time diagram time is passing as one moves from left to right.
If we "interleave" the left hands inbetween the right hands thusly:
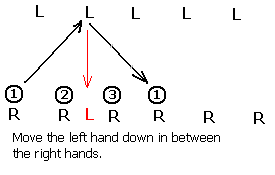
...we obtain the following diagram:
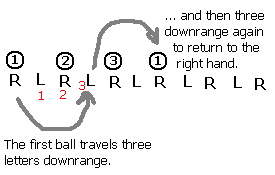
Studying the above diagram we can see that the ball moves three "hands" downrange before landing on the other hand (think of hands as landing sites, hence the use of the word site in the name of the notation). The first ball returns to the right hand after moving three more hands (or sites) rightward in the diagram.
There are three basic patterns in juggling.
In the cascade each ball follows this exact same symmetrical pattern. Mathematically this is recorded as 3 3 3 3 3 3 3 3 3... To save space, we toss the spaces and write 33333... For further simplicity we invoke a rule that number patterns repeat indefinitely, hence a single 3 can be used to denote this pattern.
Another pattern is the three ball shower, with the balls always being thrown from one hand and then caught and fed back to the first hand in a transfer. The right hand must "launch" the balls in sequence "downrange" to the opposite hand. The first opposite open "site" (hand) that permits a transfer (a throw of 1) to set up the relaunch of ball one is the fifth site.
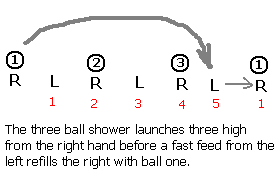
Mapping the launches and landings of the other two balls confirms that the balls land "5 site" downrange. This is refered to as a 5 1, or 51 with the spaces removed, with each ball executing the same 51 pattern over and over: 515151...
Other notes:
The notation is called site swap in part because one can "swap" or "switch around" the "sites" (hands!) on which balls land. That it, from a three ball cascade one can toss a ball from the right hand straight up, catching the ball four sites (or four counts or four beats) later. This gives one time to catch and throw a ball from the left hand while the 4 count ball is airborne. While this is happening the left hand holds onto a ball. This is counted as a "2" in the world site swaps (even numbers return to the same hand, holding a ball for an extra beat results in calling this a count of 2).
The diagram depicts a start of a three ball cascade with a single column ball off the right hand followed by a return to a three ball cascade. The notation, unsimplified, would be 33423333...
To determine the number of balls calculate the average for each sequence. Add the numbers as single digits and then divide by the number of numbers. [Note to real site swappers: this is intended as math exercise and the author does not mean to imply that this condition is by any means sufficient. It is not sufficient. The class will not be checking for multiplex landings, transition issues, or excited states.]
Determine the number of balls in the following patterns. If the mean is fractional, then the pattern does not exist or is incomplete.
Running and juggling is difficult with anything other than patterns that synchronize with the cadence of the runner. Assymetrical patterns such as 51 are very difficult to maintain while running. Since cadence is essentially a two beat, left right proposition, this author suspects that only patterns of single digits N M where N=M are really functional. This is potentially a massive limitation leaving only simple cascades as a functional possibility.
For more information and further reading see the following pages:
Siteswap FAQ by Allen Knutson
Siteswap from Wikipedia
The Invention of Juggling Notations