The numbers of Leonardo Pisano, son of Bonacci da Pisa. Leonardo was raising up his pigs, trying to figure out how many pigs he'd have in ten years if none were killed and none died. Leonardo's pigs were a breed that produced only two piglets per litter. The piglets would grow into young adults by six months and by one year old they could reproduce a pair of baby piglets.
Baby pair 
Young adult pair 
Adult breeding pair 
On the next page is a diagram of the number of pigs Leonardo had at six month intervals.
0 months: 1 pair (baby) 
Six months: 1 pair (teen) 
One year: 2 pairs (1 adult and 1 baby pair) 
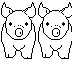


One year and a half( 18 months): 3 pairs (One adult breeding pair, one young adult, one baby )

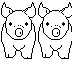


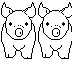
2 years (24 months): 5 pairs (two adult breeding pairs, one young adult pair, two baby pairs)
At two and half years (30 months) the pigs will no longer fit on the page. We will use three letters of the alphabet to represent each kind of pig. B will be for a Baby, Y for a young adult, and A for an adult breeder. The number of pairs is counted on the left side.
1 BB 1 YY 2 AA BB 3 BB AA YY 5 YY BB AA AA BB 8 BB AA YY AA BB AA BB YY 13 YY BB AA BB AA BB AA YY BB AA YY AA BB
At two and half years (30 months) Leonardo had 8 pairs: three adult breeding pairs, two young adult paris, and three baby paris. At three years (36 months) Leonardo had 13 pairs. So how many pairs of pigs does Leonardo have at ten years? Work in groups to determine the number of pairs at ten years. After the groups have reached their results they will report to the class their number and how they got their number.
Collect the results and then lead a group discussion on ways to get the answer. See if anyone made it to the realization that 1+1 = 2, 1 + 2 = 3, the generating function for the Fibonacci sequence. Then return to Pascal's triangle by having the student's work out the sums of the numbers in each row further below.
After the student's sum across each row, then have them add the numbers in each diagonal row. The text in the first few diagonal rows has been color coded to assist with the beginning of the job. The diagonals run from southwest to northeast. Write the answers down in order below Pascal's triangle.
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||
| 1 | 2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | |||||
| 1 | 3 | 3 | 1 | 0 | 0 | 0 | 0 | ||||||
| 1 | 4 | 6 | 4 | 1 | 0 | 0 | 0 | ||||||
| 1 | 5 | 10 | 10 | 5 | 1 | 0 | 0 | ||||||
| 1 | 6 | 15 | 20 | 15 | 6 | 1 | 0 | ||||||
| 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | ||||||
| 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 | |||||
| 1 | 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 1 | ||||
| 1 | 10 | 45 | 120 | 210 | 252 | 210 | 120 | 45 | 10 | 1 | |||
| 1 | 11 | 55 | 165 | 330 | 462 | 462 | 330 | 165 | 55 | 11 | 1 | ||
| 1 | 12 | 66 | 220 | 495 | 792 | 924 | 792 | 495 | 220 | 66 | 12 | 1 | |
| 1 | 13 | 78 | 286 | 715 | 1287 | 1716 | 1716 | 1287 | 715 | 286 | 78 | 13 | 1 |
Answers:
Row Sums:
___, ___, ___, ___, ___, ___, ___, ___, ___, ___, ___, ___, ___, ___
Diagonal sums:
___, ___, ___, ___, ___, ___, ___, ___, ___, ___, ___, ___, ___, ___
Write the next three numbers in the following sequence:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ___, ___, ___…
As a group try to work out the next three numbers in the following sequences:
3, 4, 7, 11, 18, 29, ___, ___, ___.
4, 5, 9, 14, 23, 37, ___, ___, ___.
1, 7, 8, 15, 23, 38, ___, ____, ___.
The following pattern comes from our work with Pascal's triangle and subsets, write in the next three numbers in this pattern:
1, 2, 4, 8, 16, 32, 64, ___, ____, ___.
What are the next three numbers in the following patterns?
1, 3, 9, 27, 81, 243, ___, ___, ___.
1, 4, 16, 64, 256, 1024, ___, ___, ___.
1, 7, 49, 343, 2401, 16807, ___, ___, ___.
What mathematical operation was is used to calculate the next number in the Fibonacci sequences?
____________________________________
What mathematical operation was used in the patterns such as 1, 3, 9, 27, 81, 243,….?
_________________________________
What is the next number in the sequence 1, 7, ___?
How many digits does a sequence have to have for use to predict the next number?
Make up a sequence of your own and write the first nine numbers below:
Homework:
The sum of any ten consecutive Fibonacci numbers divided by eleven is a whole number.
1 1 2 3 5 8 13 21 34 55 |
3 5 8 13 21 34 55 89 144 233 |
13 21 34 55 89 144 233 377 610 987 |
144 233 377 610 987 1597 2584 4181 6765 10946 |
610 987 1597 2584 4181 6765 10946 17711 28657 46368 |
|
Sum: |
|||||
Sum ÷ 11 |
Do you see a pattern?
What is the pattern?
What is the sum of the following ten Fibonacci numbers when divided by 11?
832040 |
1346269 |
2178309 |
3524578 |
5702887 |
9227465 |
14930352 |
24157817 |
39088169 |
63245986 |
Instructor's crib sheet:
Years |
Seq |
Fibo |
0 |
1 |
1 |
0.5 |
2 |
1 |
1 |
3 |
2 |
1.5 |
4 |
3 |
2 |
5 |
5 |
2.5 |
6 |
8 |
3 |
7 |
13 |
3.5 |
8 |
21 |
4 |
9 |
34 |
4.5 |
10 |
55 |
5 |
11 |
89 |
5.5 |
12 |
144 |
6 |
13 |
233 |
6.5 |
14 |
377 |
7 |
15 |
610 |
7.5 |
16 |
987 |
8 |
17 |
1597 |
8.5 |
18 |
2584 |
9 |
19 |
4181 |
9.5 |
20 |
6765 |
10 |
21 |
10946 |
10.5 |
22 |
17711 |
Developed by Dana Lee Ling with the support and funding of a U.S. Department of Education Title III grant and the support of the College of Micronesia - FSM. Notebook material ©1999 College of Micronesia - FSM. For further information on this project, contact dleeling@comfsm.fm Designed and run on Micron Millenia P5 - 133 MHz with 32 MB RAM, Windows 95 OS.