Suppose I walk half way towards a wall. And then I walk half of the remaining half. And then half of the half of the remaining half... how far have I walked across the room after each "half"?
The extended family of problems that include the problem are called series. Mathematically we can work out the answer in the following way:
Half way to the wall:
And then half of remaining half:
Then half of the half of the remaining
half:
Calculate the following, writing the answer as both a fraction and decimal:
=
______________(decimal form)
=
______________(decimal form)
=
______________(decimal form)
=
______________(decimal form)
Is there a pattern in the fractions? _______
What will be the fractional answer for the next sum in the series? ______
What is the decimal equivalent for the fraction above? _____
The pattern can also be written:
In advanced mathematics this is written
using the following shorthand:
If n=1 then the result is ½ or 0.5
If n=2 then the result is ¾ or 0.75
If n=3 then the result is 7/8 or 0.875... the same pattern of results as above.
Find the fractional and decimal result for n=10:
Fraction:
Decimal:
Does the series appear to be adding up to a particular number? ____
What number does this series appear to be getting closer and closer to? _____
If a series gets closer and closer to a number without passing that number the series is said to converge on that number.
To what number does it appear the series above is converging? ____
In advanced math we would write the above answer after the sum:
=
____
The above problem is part of a family of related problems. Calculate the following in decimal form:
=
___
=
___
=
___
=
______
=
______
=
______
To what does it appear this series might be adding up to? _____
=
_____
Calculate the following in decimal form:
=
___
=
___
=
___
=
______
=
______
=
______
To what does it appear this series might be adding up to (converge on)? _____
=
_____
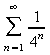What number will
converge
on? _____
Big toughie: What will
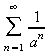converge
on? _____