Obtain as many round disks as possible. Metal washers, coffee cans, plates, cups, anything round. Have the students work in pairs. Pass the objects around from group to group. Measure the diameter d in centimeters and the circumference c in centimeters. Plot the diameter on the x-axis and the circumference on the y-axis.
If the students have only rigid rulers with which to measure, have them mark a pencil mark on rollable disks. Roll the disk one rotation along a sheet of paper. Measure the circumference on the paper.
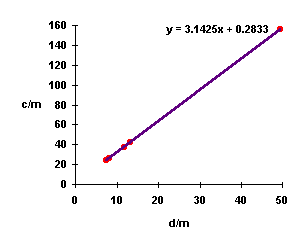
Sample data gathered by measuring round things found around the house with a cloth tape measure. Object measured included a coffee can, a coffee mug, and a fan housing.
| d/m | c/m |
|---|---|
| 7.50 | 23.8 |
| 8.20 | 26.5 |
| 11.8 | 37.2 |
| 13.3 | 41.8 |
| 49.6 | 156.2 |

Draw in a best line and determine the slope of the best line. The slope should be pi. The smallest number of significant digits in the data is three, hence the result above should contain three result digits. Pi (experimental) = 3.14 Near the end of the period find a class wide average for pi based on the results of all groups.
Fun extension: If the school has a measuring wheel (used for measuring tracks) use as long a length of fishing line or yarn as possible in an outdoor open space to roll around a center point. One student holds the yarn and stands still, others roll the wheel about the circumference. Other teams of students are tasked with determining the diameter.
Extreme extension: Obtain two wheels and have one team roll it around the circumference of the island and the other roll the wheel across a diameter of the island. See how close to pi the island is. On Pohnpei the height of the mountains will be a problem. The team crossing Nana Laud should be accompanied by experienced guides! On Moen and Kosrae the lack of a circumferential road will likely prove daunting.
Keep it simple features:
Obtain hard spheres. Golf balls, shooter marbles, ball bearings from large engines will all work well. Bigger is better, with bowling balls the best. Bowling balls will require ramp modifications. Golf balls are particularly indestructible if you can get them. Ping pong balls will not work, too light.

Make a ramp. I used a clipboard. Prop up one end of the clipboard on an official ramp propping device. I used a paperback book. Mark the floor or long table top with tape or rocks or coral pieces every 30 centimeters for about 150 centimeters. Put the zero mark at least 10 cm off the end of the clipboard. Place the ball on the clipboard and release, I used a golf ball. Use a wristwatch with a chronometer or a stopwatch or whatever device is used to time races at your school. Students may have chronographs on their watches if you are fortunate. Let the ball go. When the ball passes the 0 mark start the stopwatch or other timer. When the ball passes the 30 centimeter mark stop the timer. Repeat for a 0 to 60 cm run, 0 to 90 cm run, and on out to 150 centimeters.
| t1/s | d/m | t2/s | d/m |
|---|---|---|---|
| 0 | 0 | 0 | 0.0 |
| 0.36 | 0.3 | 0.19 | 0.3 |
| 0.66 | 0.6 | 0.48 | 0.6 |
| 1.08 | 0.9 | 0.78 | 0.9 |
| 1.42 | 1.2 | 1.16 | 1.2 |
| 1.88 | 1.5 | 1.41 | 1.5 |
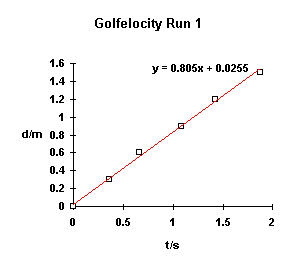
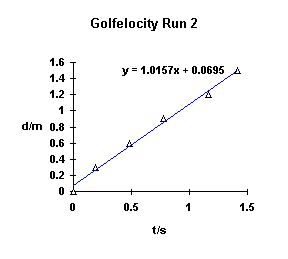
The velocity of the golf balls can be calculated from the slopes of the lines. Does the faster ball have the higher slope or lower slope value? Is the slope a constant with distance? One of the errors that can be seen for a golf ball at low velocities is the drop in speed due to friction.
Fun extension: Go outside and measure off 2 - 4 meter distances along a smooth road or parking lot. Throw the golf ball along the ground at various velocities, including as fast as possible. A golf ball works particularly nicely for this extension. Have students along the side of the path with stopwatches or chronographic watches record the time from release. The students must be careful to stand far enough clear to not get hurt by a stray bounce of the golf ball. I'd recommend the ground be swept first to remove rocks that might cause the golf ball to fly stray. Warn the students to be on their toes. I have watched youngsters launch bottle rockets at each other at New Year's and hence have some confidence that students can avoid being hit. Pick your ball pitchers well.
Keep it simple features:
Hang a fishing weight or any other compact and dense object by fishing line from a height such that the maximum length of the pendulum can be on the order of two meters. Hang them anywhere. Discretely knock a small finishing nail into the top of a door frame. Or use a sturdy light fixture. Or a beam. Use any chronograph: many digital watches have timers built in. If these are not available just use any watch that has a smallest division of seconds and take measurements to the nearest second. Time ten complete swings (ten periods) of the pendulum in seconds. Record the length L in meters and the time for ten cycles t. Calculate t and t². Graph L on the x-axis and t² on the y-axis. Fit a best line to the points. Determine the slope. The constant g can be calculated by dividing 39.5 (4π²) by the slope: g = 39.5/slope. The set-up at the right is a Kooshkin bob on a yarn line suspended from a fan hub.


One pendulum period is one swing from right to left and back to the right as seen above.
| 10t/s | t/s | L/m | t²/s² |
|---|---|---|---|
| 27.24 | 2.724 | 1.890 | 7.42 |
| 24.92 | 2.492 | 1.565 | 6.21 |
| 22.80 | 2.280 | 1.305 | 5.20 |
| 20.47 | 2.047 | 1.045 | 4.19 |
| 17.34 | 1.734 | 0.740 | 3.00 |
| 14.98 | 1.498 | 0.540 | 2.24 |
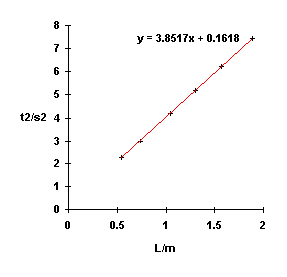
g = 39.5/3.8517 = 10.2 m/s².
The result should be on the order of 9.8 m/s². The data above led to a result that is 5% high, not bad for a Kooshkin hanging by yarn from a fan.
Fun extension: Find a really high place from which to hang a pendulum. A cliff, a palm tree, or a tall building. Do not violate private property laws or endanger yourself or your students. Measure the height. If it is a cliff you can drop a rock and time the fall and reverse engineer the height of the cliff if need be. Or if at the waterfall in Kepar, Kitti, simply toss off the least well behaved student and time their fall (check to make sure they can swim first). Have the students predict the period by calculation based on their lab data. Then time the period.
Keep it simple features:
Equipment used in the production of this page was paid for in part by a Title III grant from the United States Department of Education.
Science PrePilot Investigative Research Team
Brenna Lorenz, University of Guam
Casiano Soram, Pohnpei Islands Central School
Dana Lee Ling, College of Micronesia-FSM
Chuuk Star Support Team
Aier Willyander, FSM Dept. of Education
Joe Habuchmai, College of Micronesia-FSM
Solpisio Salvador, Pohnpei Islands Central School
Note: no kooshkin was harmed in the performance of this lab.

Return to the unofficial College of Micronesia-FSM home page
Page comments to Dana Lee Ling
Lee Ling home
page
Title III Math/Science Software Specialist
College of Micronesia-FSM
GNU GPL 1997 College of Micronesia-FSM.
Originally at (link no longer exists): http://ourworld.compuserve.com/homepages/danaleeling/cscilabs.htm