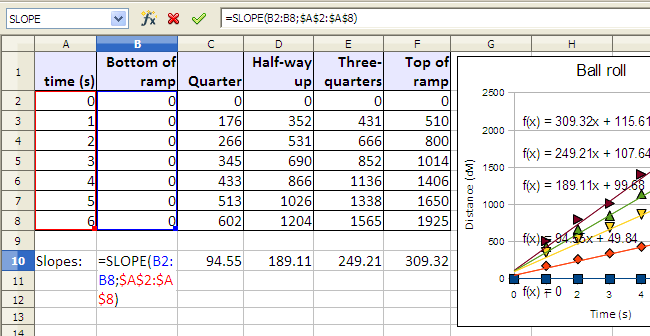
Use of mixed addressing to display multiple slopes on a spreadsheet.
Rolling balls gather no moss
Is there a linear relationship between the time and distance for a ball rolling on level ground? How does this relationship change with changes in speed?
This laboratory explores the relationship between time and distance for an object moving at a constant velocity. As noted in the first laboratory, in physical science a "relationship" means how one variable changes with respect to another variable. This change is described using mathematical equations. Math is the language in which physics is "spoken."
For a rolling ball, distance increases as time the ball rolls increases. For a ball rolling at a constant velocity (speed), this relationship is predicted to be linear. That is, a graph of time versus distance should generate a straight line. The equation that is proposed is that distance = velocity * time. If time is graphed on the x-axis and distance on the y-axis, then the slope of a line through the data should be the velocity. If a graph does not produce a line, then the hypothesis of a linear relation between time and distance is disproved for a rolling ball.
In order to produce a velocity that can be reproduced, a ball will be rolled down a ramp. This will allow "practice" runs so that timers can locate themselves near the appropriate timing mark. A student (timer) with a stop watch will call out the seconds, "One, two, three..." while watching the stopwatch. Six students will be assigned to keep track of the location of the ball at one, two, three, four, five and six seconds. The six ball trackers can use their zoris or sticks to mark the location of the ball at a particular second. Each ball tracker is responsible for a single second mark (one, two, three,... six). The key to accurately locating the ball is to watch the ball until the timer calls out the second for which the tracker is responsible. Then the tracker stops watching the ball and focuses on the spot where the ball was at that particular second. These procedure permits the experiment to proceed with a single stop watch or any other timing device that measures seconds such as a cell phone clock. This also keeps the time variable as the independent variable and the distance variable as the dependent variable.
The distance in centimeters to each timer will be recorded in the table. The experiment will be repeated and the average distance to a particular time point will be calculated.
The whole procedure will be repeated for different ball speeds to determine whether different speeds produce different slopes.
The ball will be released from the bottom of the ramp, a quarter of the way up the ramp, half-way up the ramp, three-quarters of the way up the ramp, and from the top of the ramp. The data in the table is the distance the ball has traveled after n seconds.
| time (s) | Bottom of ramp (cm) | Quarter | Half-way up (cm) | Three-quarters (cm) | Top of ramp (cm) |
|---|---|---|---|---|---|
| 0 | |||||
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| 6 |
Instructional note: If there is no access to computers, analysis can be done on graph paper. Calculators can be used if necessary. If one has no tape measure, use meter stick trees to estimate the distances. Any slope that leads to a flat, smooth area could be used.
After gathering the data, the class will go to the A204 math/science computer laboratory to determine the relationship, if any, between the time and distance for each run.
A graph is one of the first tools one uses when exploring new data. A graph will visually indicate whether a two variables are related and and what that relationship might be. Using the table above, make a single xy scatter graph. Time will be the x-axis variable, the rest of the columns will be y data. Insert linear trend lines for your data.
The velocity of the ball is the slope. The slopes on the graph may be confusing due to the number of slopes. The instructor may show you how to use a mixed absolute and relative address form of the slope function to display the individual slopes on the spread sheet.

Use of mixed addressing to display multiple slopes on a spreadsheet.
Your data will differ and your layout might be different, but for the layout shown above the function:
=SLOPE(B2:B8;$A$2:$A$8)
can be filled right to report the slope for each ball. The "dollar" signs "lock" the x-values so that as the function is copied to the right, the x-value column remains the first column.
Instructional note: One goal of this class is to improve the students ability to work with spreadsheets and spreadsheet functions.
In algebra the equation of a line is written as y = mx + b where m is the slope. In physical science the slope is usually a rate of change. In this laboratory the slope is the speed of the ball. We use the letter v for velocity (speed in a direction) in formulas.
distance d = slope (speed v) × time t
d = v × t
This sometimes written simply as d = vt
Given any time t, we can calculate the distance d. Given any distance d, can solve for the time t.
In your analysis, report the speed of the ball for each release height of the ball.
Discuss the nature of the mathematical relationship between distance and time for a rolling ball. Discuss how different starting speeds affect the slope of the relationship. Discuss whether the relationship appears to form the straight line predicted by the d = vt theory.