

Standing on a carved soap box: density of soap
Is there a linear relationship between the volume and mass for a material?
In this laboratory the mathematical relationship between the volume of a squared-off chunk of soap and the mass of the soap is explored. One result of this exploration will be a calculation of the density of the soap.
In physical science a "relationship" means how one variable changes with respect to another variable. This change is described using mathematical equations. Math is the language in which physics is "spoken."
For a physicist mathematics is not just a tool by means of which phenomena can be calculated, it is the main source of concepts and principles by means of which new theories can be created... ...equations are quite miraculous in a certain way. I mean, the fact that nature talks mathematics, I find it miraculous. I mean, I spent my early days calculating very, very precisely how electrons ought to behave. Well, then somebody went into the laboratory and the electron knew the answer. The electron somehow knew it had to resonate at that frequency which I calculated. So that, to me, is something at the basic level we don't understand. Why is nature mathematical? But there's no doubt it's true. And, of course, that was the basis of Einstein's faith. I mean, Einstein talked that mathematical language and found out that nature obeyed his equations, too. – Physicist Freeman Dyson
A core concept in the physical sciences is the idea that physical systems obey mathematical equations. The mathematical equations are also called mathematical models or mathematical relationships.. If two variables are related by a mathematical equation, then predictions can be made about that physical system. Physics, engineering, and chemistry all depend on predictable results. When something is done in the same way twice, the same result should occur.
One way to begin to find the mathematical equation that relates two variables is to make an xy scatter graph. The graph will help indicate whether a relation exists between the variables. The graph will also help us determine the nature of the relationship. By nature we mean whether the relationship is linear or non-linear.
If the relationship is linear or non-linear, then the system behaves in a predictable manner. Given the value of one variable, we can predict the value of the other variable. In this class we will only try to make predictions for linear relationships. Non-linear relationships are also predictable, but the mathematics is beyond the scope of this course.
If the relationship is linear, then the equation has the form y = startValue + Rate * x. You may be more familiar with the form y = mx + b. In physics the slope m is often a rate of change and the y-intercept b is often a startValue. The y-intercept is not always the startValue, but for many systems the y-intercept, where x = 0, is a starting place for a system.
If we find that a relationship does form a roughly straight line, then we will try to find the slope and intercept.
The following graphs show the different types of relationship that might exist between two variables.
To decide on whether a relationship exists between two variable start with an xy scattergraph. Looking at the graph, consider the following questions:
If the data points form roughly a straight line, then use the spreadsheet function SLOPE and INTERCEPT to obtain the slope and intercept. The slope and intercept can also be displayed on the graph directly. If the data points form a smooth curve, then the relationship is a non-linear relationship. Determining the nature of the relationship may or may not be possible for us in this course. If the data points form no pattern, then there is no relationship between the variables being studied.
The following decision flow chart is a map of the flow of decisions described above.
The functions provided in the above chart are specified in more detail below. The format shown is the OpenOffice.org Calc format. If using Excel, substitute commas for the the semi-colons. Ubuntu 9.04 with OpenOffice.org 3.0 also uses commas instead of semi-colons. Your instructor can inform you which form is appropriate for the software you are using.
The following two functions calculate the slope and intercept for any linear relationship.
=SLOPE(y-data;x-data)
=INTERCEPT(y-data;x-data)
If the data points form a line, then we can draw a line through the points. This line that best goes through the data points is called a best fit line, trend line, or a linear regression. The functions above calculate the slope and intercept for this line through the data points. Linear regressions are an important mathematical tool in the physical sciences.
Note that because of uncertainty in primary measurements and error, data is considered linear even when the data falls only roughly along a straight line. The data does not have to fall exactly in a straight line. The issue of how close data comes to a straight line is part of the study of correlation in statistics.
In this laboratory you will explore the relationship between volume and mass for soap. You will measure the length, width, and height of a soap slab, calculate the volume of soap slab, and measure the mass of the soap slab. A graph of volume versus mass will be made. If a relationship is found, then the mathematical equation of the relationship will be calculated. Remember, "a relationship" simply means that a pattern such as a line or curve is formed on an xy scattergraph of the two quantities. That relationship is usually expressed as a trend line. The slope of the trend line will have a physical meaning.
Run a demonstration density calculation using the wood alphabet block and a lead cube. Ask the class to predict the result prior to putting the object in water.
The equation:
is of the form
where volume is x, mass is y, and the density is the slope m.
The theory behind this laboratory is that the slope of the linear regression line for the volume versus the mass is the density. According to theory, density should be the same for a substance no matter whether the piece is large or small. If this is true, then a plot of volume versus mass should produce a straight line with a slope equal to the density.
In this laboratory the units of mass are grams, the units of volume are cubic centimeters, and the units of density are grams per cubic centimeter.
Length, width, height, and mass are fundamental quantities. Both volume and density are "derived" quantities.


| Length (cm) | Width (cm) | Height (cm) | Volume [x] (cm³) | Mass [y] (g) |
|---|---|---|---|---|
Note: Do not put units into the table. The units are stated in the first row of the table. In a table the units only appear in the first row, the head row.
In the computer laboratory we will make a graph with volume on the x-axis and mass on the y-axis. Then we will run a mathematical decision analysis and make the appropriate calculations of the slope and the y-intercept using a spreadsheet. If the density relationship holds true, then the slope will be the density of the soap.
Select the two columns containing the x and y data. Note that the x data column is on the left, the y data is in the column on the right. Do not put blank columns or rows into the middle of a data table.
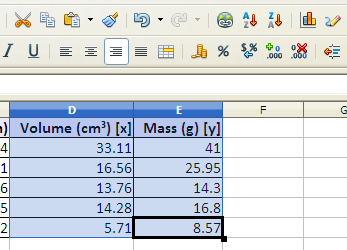
Data table
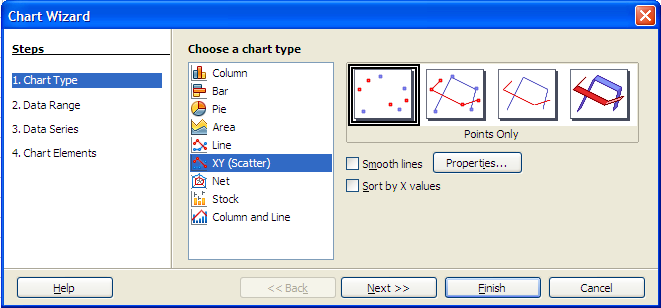
Choose xy scatter graph in step one.
Click next until you reach step four.
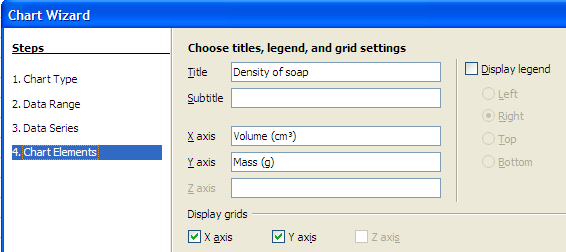
In step four, add titles.
Immediately after clicking on the Finish button, choose Insert: Trend Lines.
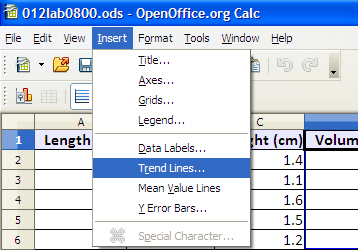
Insert: Trend Lines
If the data appears to scatter along a straight line, choose a linear regression. Click on the check box at the bottom to show the equation of the line including the slope and intercept.
Linear regression dialog box
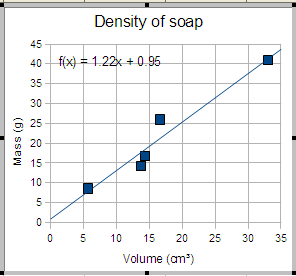
Resulting graph with equation
If you forgot to insert the trend line immediately after creating the chart, then you have to double-click on the chart to obtain the insert menu which includes the trend lines item.
Report the results of your analysis above. Include the slope and the units for the slope. Explain the physical meaning of the slope. Note that the units for the y-intercept are not the same as the units for the slope. When reporting the y-intercept, the units are the same as those on the y-axis.
Report the mathematical relationship of volume and mass, including both the slope and intercept. Discuss the physical meaning of the slope.
Mathematical relationships allows us to make predictions.
The density of water is close to 1.0 g/cm³ If the density of an object is greater than one, then the object will sink. If the density is less than one, then the object will float. Can you predict whether the soap you carved will float or sink? Why or why not?
Use a spreadsheet and/or word processing package to type up a report with the sections seen above. Include your tables. The class will spend the final portion of the period in A204 to learn how to do this. Laboratory reports are due a week later at the NEXT laboratory period. Laboratory reports submitted after the start of the next laboratory are late. The lab report can be submitted as either a hard copy from a printer or via email. Put your name on the report!
To send a report via email you must attach the report to either your comfsm, Yahoo, Gmail, or other on line account. Do NOT use "File: Send to" as the report will not get sent anywhere on most college computers. Most on line email systems have a system where you can select an attachment (your report) and then add that attachment to the email.
If you start your report in the A204 computer laboratory and intend to continue work in the library, use "Save as" and set the file type to "Excel". The library does not have OpenOffice.org installed as of mid-2008.