In this activity we will explore the shape of the path through the air made by a sphere. The path is a path in two-dimensional space. The graph will be a space versus space graph using the MKS system.
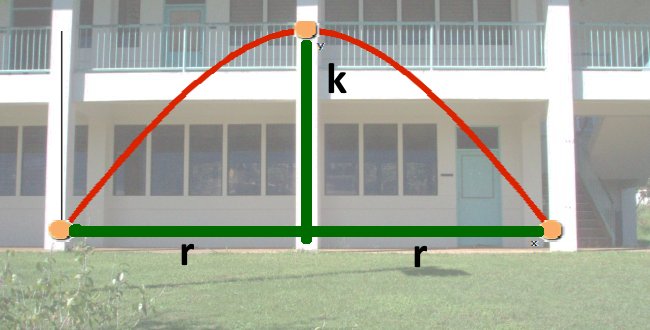
We will be working outside to measure the arc of the sphere. The set-up and variables to be measured are seen in the following diagram.

Where k is the height of the y-intercept above the x-axis
and r is the distance from the axis of symmetry to one x-intercept (root).
| Task | n | Position title | Student name | x | y |
|---|---|---|---|---|---|
| Right x-intercept | 1 | Ball underhand pitcher | |||
| 2 | Meter stick holder | ||||
| 3 | Recorder | ||||
| right mid arc height | 4 | Tape measure holder | x | y | |
| 5 | Tape base holder | ||||
| 6 | arc height observer | ||||
| 7 | Data recorder | ||||
| Vertex height k | 8 | Tape measure holder | Same as 4 | x | y |
| 9 | Tape base holder | Same as 5 | |||
| 10 | Vertex position observer | ||||
| 11 | Data recorder | ||||
| left mid arc height | 12 | Tape measure holder | x | y | |
| 13 | Tape base holder | ||||
| 14 | arc height observer | ||||
| 15 | Data recorder | ||||
| Left x-intercept | 16 | Ball catcher | x | y | |
| 17 | Meter stick holder | ||||
| 18 | Recorder | ||||
| x-intercept to x-intercept | 19 | Wheel roller | distance = 2r | ||
| 20 | Recorder | ||||
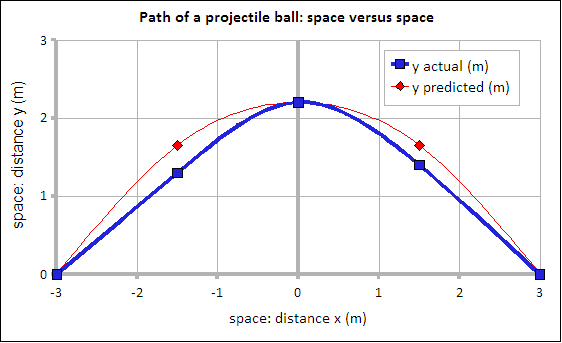
Does our data agree with the theory? Use a spread sheet to plot the data. Set up a table like the seen below for spring 2008. Make an xy scattergraph of all three columns. Use the k and r from the activity to calculate the predicted path. The function below is an example based on the spring 2008 data. Your values of k and r will be different. Spring 2008 k was 2.2 m and r was 3.0 meters. The presumes that the column titles are in row 1 and that the first x-value is in cell A2. This formula would be in C2 and can be "filled down" for the next four rows.
=-(2.2/(3.0^2))*A2^2+2.2
Data from spring 2008
| location x (m) | y1 actual height (m) | y2 predicted height using the equation(m) |
|---|---|---|
| -3.0 | 0.0 | 0.00 |
| -1.5 | 1.3 | 1.65 |
| 0.0 | 2.2 | 2.20 |
| 1.5 | 1.4 | 1.65 |
| 3.0 | 0.0 | 0.00 |