Using Mathview To Solve Logarithmic Equations
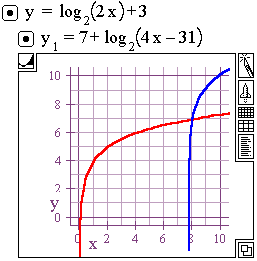
The graph of a function f(x) and another function g(x) intersect at the place where the two functions produce the same output for a common input. On the graph below the functions f(x) = log2(2x) +3 and g(x) = 7 + log2(4x – 31) appear to cross at the coordinates x = 8 and y = 7. That is, an input of x = 8 into either function appears to produce a common result of 7.
Note that MathView does not accept f(x) and g(x) notation, so f(x) is y and g(x) is y1 in the example below.

To determine if the intersection coordinates are actually (8, 7) the two functions are set equal to each and then solved for x. The problem is:
Solve for x: log2(2x) + 3 = 7 + log2(4x – 31)
The following laboratory is designed to assist in learning how to use MathView to enter and solve such an equation.
Open MathView with a blank notebook.
Begin by typing in: log2(2x) + 3 and g(x) = 7 + log2(4x – 31). To do this type (no spaces!):
log2(2*x) + 3 = 7 + log2(4*x–31)
The is done by holding down the shift key and pressing the minus sign key to the left of the Backspace key on the alphabetic keyboard.
The escape key is in the upper left corner of the keyboard and is used to "escape" from subscripts, exponential superscripts, and denominators.
The result should be:
MathView can be used to re-manipulate the equation and thus solve for x. The process is the same as the one we use on paper, but the computer handles the arithmetic for us.
Isolate the exponential or logarithmic function.
This is done by "dragging" the functions to the left side of the equation and all other constants and coefficients to the right side of the equation. Start by selecting the left side logarithm by dragging the mouse across the logarithm. The result will look like:
![]()
Now hold down the control key, click on the blue area, and drag the log to the left side of the equation. Release the mouse button. The result should be:
![]()
Click the mouse to left of the constant 3 on the left side of the equation and select the 3 by dragging across the 3.
![]()
Drag the the 3 to the right side of the equation. The result should be:
![]()
Select only the left side of the equation by dragging the mouse across the left side:
![]()
Choose the Manipulate menu. Look for the item Other on the Manipulate menu. Click on other. A submenu will appear. The sixth item down will be commute. Roll down to commute and click on it. The result should be:
![]()
Choose Collect from the Manipulate menu to get:
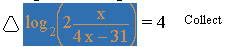
Invert the expression by isolation
Now select the variable fraction expression as seen below. The easiest way to select the fraction is to click directly on the fraction bar. This may take some practice, the result will look like:
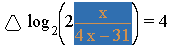
Hold down the control key and drag the fraction to the right triangle. When the triangle turns black:
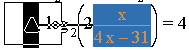
release the mouse button to get:
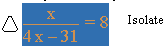
Solve for x
With the whole expression selected (as seen immediately above), choose from the Manipulate Menu the item Apply (seventh down the list). The appearance will change to:
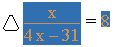
Type the following exactly:
*(4*x–31)
To get:
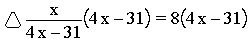
Now click on the equals sign to get:
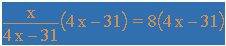
Then choose from the Manipulate menu the item Expand (the third down from the top) to get:
![]()
Select the x on the left side to get:
![]()
Now drag the x to the right side to obtain:
![]()
Now select the x and drag it to the triangle on the left ![]() to get:
to get:
![]()
Finding y by substituting x into one of the functions:
To find y press the Enter key on the alphabetic keyboard to get a new blank square:
![]()
Enter log2(2x) + 3 by typing log2(2*8) + 3 to get
![]()
Select the equation by dragging the mouse across it and then choose calculate from the Manipulate menu.
![]()
The result confirms the appearance of the graph : X = 8 and y =7
Review:
The key steps to solving an exponential/ logarithmic expression are to:
Isolate the logarithmic function
Invert
Isolate the x.
Solve the following expressions for x using MathView:
log3(3x) = 2
log4(2x+8) = 6
ln(x4) – ln(7) = 1
ln(x) + 3 = 7 + ln(4x – 31)