The students will learn another way to think of numbers, linking numbers to non-counting concepts. The object is to enrich their thinking about numbers, to break the students away from seeing numbers as existing only in arithmetic contexts. In a class with stronger English skills or with strong math skills one might try having the students obtain formulas for the numbers of a given shape.
In MS 050 Fall 96 this was used after Pigonacci to get at the meaning of prime factorization, which we will then use to perform canceling in Fibobellian fractions.
A number is even if it can be lined up in two rows of equal length:
2 0 0
4 00 00
6 000 000
8 0000 0000
10 00000 00000
A number is odd if it cannot be lined up in two rows of equal length:
1 0
3 00 0
5 000 00
7 0000 000
A number is square if it can make a square:
1 0
4 0 0 0 0
9 0 0 0 0 0 0 0 0 0
A number is rectangular if it can make a rectangle:
2 0 0
6 0 0 0 0 0 0
8 0 0 0 0 0 0 0 0
10 0 0 0 0 0 0 0 0 0 0
A number is triangular if it can make a triangle:
3 0 0 0
6 0 0 0 0 0 0
10 0 0 0 0 0 0 0 0 0 0
A number is composite if it can be made into a square or rectangle with more than one row:
4 0 0 0 0
6 0 0 0 0 0 0
8 0 0 0 0 0 0 0 0
9 0 0 0 0 0 0 0 0 0
10 0 0 0 0 0 0 0 0 0 0
12 0 0 0 or 0 0 0 0 or 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
A number is prime if it cannot be made into a square or rectangle with more than one row. Prime numbers can only be a single row, a single row is a line. All numbers that are not composite are prime.
1 0 (prime because it is only one row)
2 0 0 (prime because it is a one row rectangle, or only a one column rectangle if turned)
3 0 0 0 0 0 ( prime: cannot be made into a multi-row rectangle) 0
5 0 0 0 0 0 0 0 0 0 0
7 0 0 0 0 0 0 0
11 0 0 0 0 0 0 0 0 0 0 0
As a group finish filling in the blanks in the following chart. Use drawings to help you decide. Due to implementations of CSS in browsers the gridlines will not appear in the empty cells.
| Even | Odd | Square | Rectangle | Triangle | Composite | Prime | |
| 1 | no | yes | yes | no | no | no | yes |
| 2 | yes | no | no | yes | no | no | yes |
| 3 | no | yes | no | no | yes | no | yes |
| 4 | yes | no | yes | no | no | yes | no |
| 5 | no | yes | no | no | no | no | yes |
| 6 | yes | no | no | yes | yes | yes | no |
| 7 | no | yes | no | no | no | no | yes |
| 8 | yes | no | no | yes | no | yes | no |
| 9 | no | yes | yes | no | no | yes | no |
| 10 | yes | no | no | yes | yes | yes | no |
| 11 | yes | ||||||
| 12 | yes | ||||||
| 13 | |||||||
| 14 | |||||||
| 15 | |||||||
| 16 | |||||||
| 17 | |||||||
| 18 | |||||||
| 19 | |||||||
| 20 | |||||||
| 21 | |||||||
| 22 | |||||||
| 23 | |||||||
| 24 | |||||||
| 25 | |||||||
| 26 | |||||||
| 27 | |||||||
| 28 | |||||||
| 29 | |||||||
| 30 | |||||||
| 31 | |||||||
| 32 | |||||||
| 33 | |||||||
| 34 | |||||||
| 35 | |||||||
| 36 | |||||||
| 37 | |||||||
| 38 | |||||||
| 39 | |||||||
| 40 | |||||||
| 41 | |||||||
| 42 |
What is the smallest odd composite number that is not a square? _____
Is any number listed both a square number and a rectangular number? _____
If there is a square number and a rectangular number, what is it? _____
Is any number listed both a square number and a prime number? _____
If there is a square number and a prime number, what is it? _____
Is any number listed both a triangular number and a square number? _____
If there is a triangular number and a square number, what is it? _____
Is any number listed triangular, square, and rectangular? _____
If there is a triangular, square and rectangular number, what is it? _____
List the line (prime) numbers up to 42: ______________________________
List the triangle numbers up to 42: ______________________________
List the square numbers up to 42: ______________________________
List the rectangle numbers up to 42: ______________________________
As a group agree on a shape that is not listed above. Shape: _____
What is the first number of that shape? _____
What is the second number of that shape? _____
What is the third number of that shape? _____
What is the fourth number of that shape? _____
What is the fifth number of that shape? _____
HW: What is the smallest square that is the sum of two other squares? _____
At the end of the class have each group present its shape and the first three numbers of its shape.
Teacher's note: The non-specification and non-introduction of further shapes is intentional. The idea is to reveal to the teacher the student's thinking about shapes. Do the student's use higher order polygons? Do they go three-dimensional? Do they choose non-convex polygons? If they choose a polygon, how did they choose to generate the nth number? The openness is intentional. This is why it is a group activity, for alone the students might stump and stall. The group should provide the necessary safety and creativity to generate some form of answer.
Teacher's note for advanced classes: The triangular numbers of the sum of consecutive integers from 1 to n, hence the sum formula (n/2)(n+1) yields the nth triangular number. For square numbers one can use the square formula, although it also the sum of every other number, 1+3+5… For pentagonal one adds every third number. The general formula for the nth r-agonal number is (n/2)[2 + (n-1)(r-2)]. This formula ought never be presented to the students to learn by memorization. That would miss the point. The point would be to spend a couple weeks learning problem solving by having the groups try to find formulas for each consecutive shape. Groups would be asked to work in English to reinforce that which is the goal of the IEP: English acquisition. The real goal of this would be the simultaneous acquisition of English and inquiry skills.
| Triangle | Square | Pentagonal | Hexa | Hepta | Octa | Nona | Deca | Cubics | HyperCubics | ||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 8 | 16 | |
| 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 27 | 81 | |
| 4 | 10 | 16 | 22 | 28 | 34 | 40 | 46 | 52 | 64 | 256 | |
| 5 | 15 | 25 | 35 | 45 | 55 | 65 | 75 | 85 | 125 | 625 | |
| 6 | 21 | 36 | 51 | 66 | 81 | 96 | 111 | 126 | 216 | 1296 | |
| 7 | 28 | 49 | 70 | 91 | 112 | 133 | 154 | 175 | 343 | 2401 | |
| 8 | 36 | 64 | 92 | 120 | 148 | 176 | 204 | 232 | 512 | 4096 | |
| 9 | 45 | 81 | 117 | 153 | 189 | 225 | 261 | 297 | 729 | 6561 | |
| 10 | 55 | 100 | 145 | 190 | 235 | 280 | 325 | 370 | 1000 | 10000 |
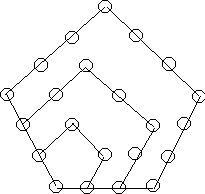
Pentagonal sample:

Note that for the convex two-dimensional polygonal numbers the number of elements added on a side is considered to increase by one (see also a square). Thus a pentagon expands five sides (two can remain co-linear while three expand "in space"), adding one element to each side as it goes. The result is that the number added with each expansion is 1, 4, 7, 10, 13, 16… or 3n + 1 where n is an index value. Adding these number produces the pentagonal numbers:
1, 5, 12, 22,…
Developed by Dana Lee Ling with the support and funding of a U.S. Department of Education Title III grant and the support of the College of Micronesia - FSM. Notebook material ©1999 College of Micronesia - FSM. For further information on this project, contact dleeling@comfsm.fm Designed and run on Micron Millenia P5 - 133 MHz with 32 MB RAM, Windows 95 OS.