Along with Gnuplot, I also use Maxima as a tool to quickly explore sets of algebra problems and confirm answer keys. The package is open source, cross-platform, and free. Maxima is based on the precursor to packages such as Mathematica and Maple, hence Maxima will be most familiar to users of those packages.
Maxima is very literal, a single misplaced comma, a forgotten semi-colon, or using implicit multiplication will throw a cryptic error message. Mathematics is about precision, and Maxima is no exception to that rule. The following screen shows a short Maxima session.

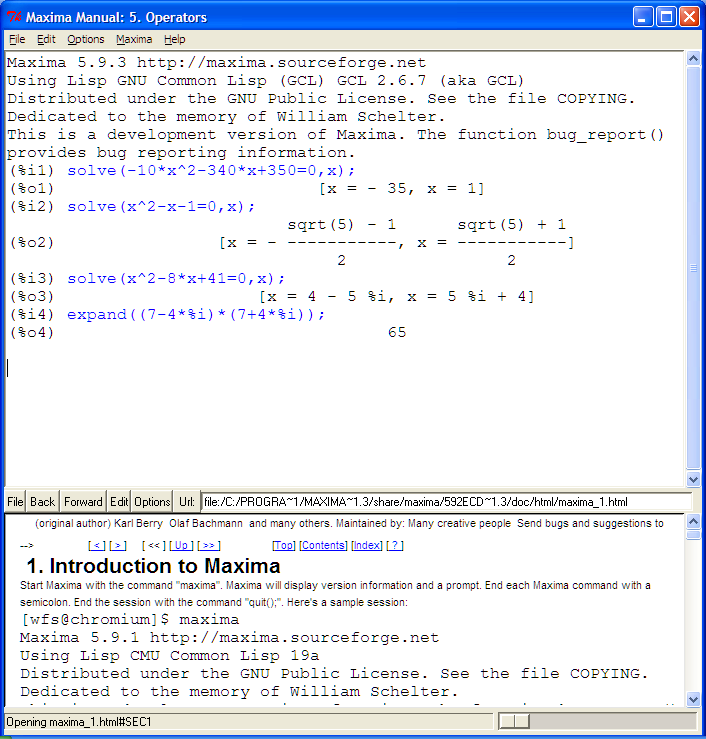
Maxima is a command line oriented program. Single line commands are input via the keyboard and Maxima responds with an output. In the image the lines prefixed %i are inputs, %o are outputs.
Some basic commands can be seen above, for clarity I repeat them below. Note that %i is an imaginary i, %pi is used for pi.
(%i1) solve(-10*x^2-340*x+350=0,x); (%o1) [x = - 35, x = 1] (%i2) solve(x^2-x-1=0,x); sqrt(5) - 1 sqrt(5) + 1 (%o2) [x = - -----------, x = -----------] 2 2 (%i3) solve(x^2-8*x+41=0,x); (%o3) [x = 4 - 5 %i, x = 5 %i + 4] (%i4) expand((7-4*%i)*(7+4*%i)); (%o4) 65 (%i5) factor(x^2-3*x-10); (%o5) (x - 5) (x + 2)
One of the strengths of packages such as Maxima is that an output can be used as an input by referencing the line number.
(%i4) expand(-k/(r*s))*(x-r)*(x-s); k (x - r) (x - s) (%o4) - ----------------- r s (%i5) expand(%o4); 2 k x k x k x (%o5) - ---- + --- + --- - k r s s r
Note that the %o4 told Maxima to expand output number four. Maxima has extensive help files. Finding what a beginner needs and wants, however, may be difficult. One can, by wandering through the manual, see examples and get an idea of how to perform various operations with Maxima. Maxima can differentiate, integrate, and perform many other complex operations symbolically.