MS 100 Midterm Examination 07 March 2006 • Name:
1. Find the center (h, k) and radius of the circle (x − 14 )² + (y + 851)² = 900
2. For y = x² − 14x − 851
a. Find the y-intercept.
b. Find the x-intercepts.
c. What line is the graph symmetric about?
d. Use the above information and the type of equation to sketch a graph of the equation.
e. Does the graph pass the vertical line test?
f. Is the equation a function?
g. Mark the increasing and decreasing intervals on the graph.
h. Mark the sections, if any, of positive and negative curvature on the graph.
i. Mark the local minimum and maximums, if any, on the graph.
j. Use the x-intercepts to determine the factorization of the equation.
k. Does the equation have a slope?
3. Solve for x: 7x² − 98x + 6643 = 0
4. Multiply the following complex conjugates: (7 + 30i)(7 − 30i)
5.
Solve for x:
![]()
6.
Solve the inequality and sketch the solution on a number line:
![]()
7. Find the equation of the line through (− 41, 19) and (-37, 41)
8. Is y = −5.5x + 244.5 parallel, perpendicular, or neither to the line in 7?
9.
Is
![]() parallel, perpendicular, or neither to the line in 7?
parallel, perpendicular, or neither to the line in 7?
10. On a Tuesday evening last summer I was running and juggling back northbound into Piyuul from the Malem river bridge. I took 10.8 minutes to run the 1.826 kilometers.
a. Given that pace = time/distance, what was my pace on that Tuesday in minutes per kilometer?
b. I usually run and juggle (joggle) at a 6.5 minute per kilometer pace. Was I slower or faster on Tuesday evening than my usual pace?
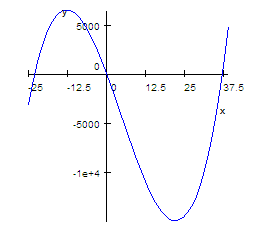
11. a. Is the function depicted in the graph a constant, linear, quadratic, or cubic function?
b. How many zero's does the function have?